云南省楚雄州双柏县2023年中考二模数学试卷

试卷更新日期：2023-06-19 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 2023$ 的倒数是（）

A、 $- 2023$ B、2023 C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
2. 2023年2月28日，国家统计局发布《中华人民共和国2022年国民经济和社会发展统计公报》．初步核算2022年末全国人口141175万人，数据141175万用科学记数法表示为（）

A、 $1.41175 \times 1 0^{8}$ B、 $1.41175 \times 1 0^{9}$ C、 $14.1175 \times 1 0^{8}$ D、 $1.41175 \times 1 0^{5}$

查看试题解析
3. 下列图形既是轴对称图形，又是中心对称图形的是（）

A、等边三角形 B、等腰三角形 C、平行四边形 D、菱形

查看试题解析
4. 某几何体从三个不同方向看到的图形形状如图所示，那么该几何体是（）

A、圆柱体 B、长方体 C、正方体 D、四棱柱

查看试题解析
5. 一元二次方程 $x^{2} - 2 x + a = 0$ 的一根是 $3$ ，则另外一根是（）

A、 $3$ B、 $1$ C、 $- 3$ D、 $- 1$

查看试题解析
6. 正六边形的外角和为（）

A、 $120 °$ B、 $180 °$ C、 $360 °$ D、 $720 °$

查看试题解析
7. 按一定规律排列的单项式： $- x ， 5 x^{2} ， - 9 x^{3} ， 13 x^{4} ， - 17 x^{5}$ ， …，第n个单项式是（）

A、 $(5 n - 4) {(- x)}^{n}$ B、 $(5 n - 4) x^{n} +$ C、 $(4 n - 3) x^{n}$ D、 $(4 n - 3) {(- x)}^{n}$

查看试题解析
8. 已知反比例函数 $y = - \frac{2}{x}$ 的图象过点 $P (a ， b)$ ，则代数式 $a b$ 的值为（）

A、 $- 2$ B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
9. 如图， $A D$ 是 $△ A B C$ 的外接圆 $⊙ O$ 的直径，若 $∠ D A B = 62 °$ ，则 $∠ A C B$ 的度数为（）

A、 $20 °$ B、 $28 °$ C、 $38 °$ D、 $62 °$

查看试题解析
10. 某学习小组10名学生参加“数学课后训练”，他们的得分情况如下表：
人数（人）
1
4
3
2
分数（分）
80
90
85
95
那么这10名学生所得分数的众数和中位数分別是（）

A、90，90 B、90，85 C、90，87.5 D、85，85

查看试题解析
11. 如图，在纸上剪一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型，若圆的半径 $r = 2$ ，扇形的圆心角等于 $90 °$ ，则围成的圆锥的母线长R的值为（）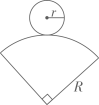

A、2 B、4 C、8 D、10

查看试题解析
12. 为推进垃圾分类，推动绿色发展，某化工厂要购进甲、乙两种型号机器人用来进行垃圾分类，用360万元购买甲型机器人和用480万元购买乙型机器人的台数相同，两种型号机器人的单价和为140万元，若设甲型机器人每台x万元．根据题意，所列方程正确的是（）

A、 $\frac{360}{x} = \frac{480}{140 - x}$ B、 $\frac{360}{140 - x} = \frac{480}{x}$ C、 $\frac{360}{x} + \frac{480}{x} = 140$ D、 $\frac{480}{x} - \frac{360}{x} = 140$

查看试题解析

二、填空题

13. 分解因式： $a b^{2} - a^{2} b + a b$ ＝．

查看试题解析
14. 如图， $A B ∥ C D$ ，若 $∠ C E F = 60 °$ °，则 $∠ F A B$ 的度数为．

查看试题解析
15. $\sqrt[3]{- 8} - \sqrt{4} =$ ．

查看试题解析
16. 已知等腰三角形的两边长分别为5和8，则这个等腰三角形的周长为．

查看试题解析

三、解答题

17. 化简： $(\frac{1}{x + 1} - \frac{1}{x - 1}) \div \frac{2}{1 - x}$

查看试题解析
18. 如图， $A C$ 与 $B D$ 相交于点O，且 $A B = D C$ ， $A C = D B$ ．求证： $O B = O C$ ．

查看试题解析
19. 从2021年秋季开学以来，全国各地中小学都开始实行了“双减”政策．为了解家长们对“双减”政策的了解情况，从某校1200名家长中随机抽取部分家长进行问卷调查，调查评价结果分为“了解较少”“基本了解”“了解较多”“非常了解”四类，并根据调查结果绘制出如图所示的两幅不完整的统计图．

(1)、本次抽取家长共有人，扇形图中“基本了解”所占扇形的圆心角是．

(2)、估计该校“非常了解”和“了解较多”的家长共有多少人？

查看试题解析
20. 小明和小华想利用抽取扑克牌游戏决定谁去参加市里举办的“创建全国文明城市，争做文明学生”的演讲比赛，游戏规则是：将4张除了数字2、3、4、5不同外，其余均相同的扑克牌，数字朝下随机平铺于桌面，一人先从中随机取出1张，另一人再从剩下的3张扑克牌中随机取出一张，若取出的2张扑克牌上数字和为偶数，则小明去参赛，否则小华去参赛．

(1)、用列表法或画树状图法，求小明参赛的概率；

(2)、你认为这个游戏公平吗？请说明理由．

查看试题解析
21. 如图， $A E ∥ B F$ ，将 $△ A B C$ 绕点C顺时针旋转60°后得到 $△ D A C$ ，点A、B的对应点分别是点D、A， $A C$ 与 $B D$ 相较于点O．

(1)、求证：四边形 $A B C D$ 是菱形；

(2)、若 $A C = 4$ ，求四边形 $A B C D$ 的面积．

查看试题解析
22. 某公司计划组织员工360人去华为公司参观学习，经过研究，决定从当地租车公司提供的A，B两种型号客车中，租用20辆作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息：

型号

载客量

租金单价

A

20人/辆

300元

B

15人/辆

200元

注：载客量指的是每辆客车最多可载该校师生的人数.

设学校租用A型号客车x辆，租车总费用为y元.

(1)、求y与x的函数关系式，并直接写出x的取值范围；

(2)、若要使租车总费用不超过 $5800$ 元，一共有几种租车方案？并求出最低租车费用.

查看试题解析
23. 已知二次函数 $y = - x^{2} + 6 x - 5$

(1)、当 $1 \leq x \leq 4$ 时，函数的最大值和最小值分别为多少？

(2)、当 $t ≤ x ≤ t + 3$ 时，函数的最大值为 $m$ ，最小值为 $n$ ，若 $m - n = 3$ ，求 $t$ 的值．

查看试题解析

人数（人）	1	4	3	2
分数（分）	80	90	85	95

型号	载客量	租金单价
A	20人/辆	300元
B	15人/辆	200元