2023年浙教版数学九年级上册第一章 二次函数 单元测试(提高版)
试卷更新日期:2023-06-18 类型:单元试卷
一、单选题(每题2分,共20分)
-
1. 已知关于的二次函数解析式为 , 则( )A、±2 B、1 C、-2 D、±12. 函数的图象是由函数的图象轴上方部分不变,下方部分沿轴向上翻折而成,如图所示,则下列结论正确的是( )
① ;②;③;④将图象向上平移1个单位后与直线有3个交点.
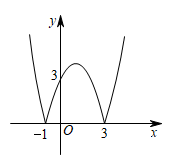 A、①② B、①③ C、②③④ D、①③④3. 已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x1 , 0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方.下列结论:①a<b<0;②4a+2b+c>0;③2a+c>0;④2a-b+1>0,其中符合题意结论的个数是( )A、4个 B、3个 C、2个 D、1个4. 若平面直角坐标系内的点 满足横、纵坐标都为整数,则把点 叫做“整点”.例如: 、 都是“整点”.抛物线 与 轴交于A、 两点,若该抛物线在A、 之间的部分与线段 所围成的区域(包括边界)恰有七个整点,则 的取值范围是( )A、 B、 C、 D、5. 如图,抛物线交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.
A、①② B、①③ C、②③④ D、①③④3. 已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x1 , 0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方.下列结论:①a<b<0;②4a+2b+c>0;③2a+c>0;④2a-b+1>0,其中符合题意结论的个数是( )A、4个 B、3个 C、2个 D、1个4. 若平面直角坐标系内的点 满足横、纵坐标都为整数,则把点 叫做“整点”.例如: 、 都是“整点”.抛物线 与 轴交于A、 两点,若该抛物线在A、 之间的部分与线段 所围成的区域(包括边界)恰有七个整点,则 的取值范围是( )A、 B、 C、 D、5. 如图,抛物线交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.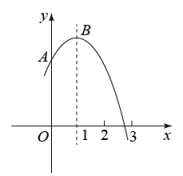
①一元二次方程有两个相等的实数根;②若点 , , 在该函数图象上,则;③将该抛物线先向左平移1个单位,再沿x轴翻折,得到的抛物线表达式是;④在y轴上找一点D,使的面积为1,则D点的坐标为.以上四个结论中正确的个数是( )
A、1个 B、2个 C、3个 D、4个6. 已知二次函数y=(x-m+2)(x+m-4)+n,其中m,n为常数,则( )A、m>1,n<0时,二次函数的最小值大于0 B、m=1,n>0时,二次函数的最小值大于0 C、m<1,n>0时,二次函数的最小值小于0 D、m=1,n<0时,二次函数的最小值小于07. 如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1 , 将C1向右平移得C2 , C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )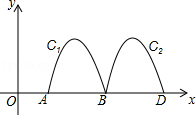 A、 B、 C、 D、8. 已知二次函数 , 与的部分对应值为:
A、 B、 C、 D、8. 已知二次函数 , 与的部分对应值为:-2
-1
0
1
2
-1
2
3
2
?
关于此函数的图象和性质,下列说法正确的是( )
A、当时,函数图象从左到右上升 B、抛物线开口向上 C、方程的一个根在-2与-1之间 D、当时,9. 已知二次函数与一次函数交于、两点 , 当时,至少存在一个x使得成立,则m的取值范围是( )A、 B、 C、 D、10. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、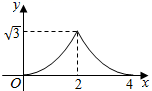 B、
B、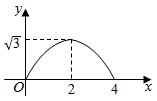 C、
C、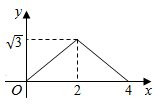 D、
D、
二、填空题(每空3分,共18分)
-
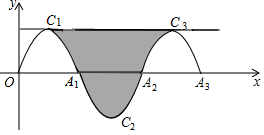
11. 已知一个二次函数的图象经过点 , 且在轴左侧部分是上升的,那么该二次函数的解析式可以是(只要写出一个符合要求的解析式).12. 如图,一段抛物线: ,记为 ,它与x轴交于两点O, ;将 绕 旋转 得到 ,交x轴于 ;将 绕 旋转 得到 ,交x轴于 ,过抛物线 , 顶点的直线与 、 、 围成的如图中的阴影部分,那么该阴影部分的面积为.
 13. 如图,已知二次函数 的图象与 轴交于不同两点,与 轴的交点在 轴正半轴,它的对称轴为直线 .有以下结论:① ,② ,③若点 和 在该图象上,则 ,④设 , 是方程 的两根,若 ,则 .其中正确的结论是(填入正确结论的序号).
13. 如图,已知二次函数 的图象与 轴交于不同两点,与 轴的交点在 轴正半轴,它的对称轴为直线 .有以下结论:① ,② ,③若点 和 在该图象上,则 ,④设 , 是方程 的两根,若 ,则 .其中正确的结论是(填入正确结论的序号).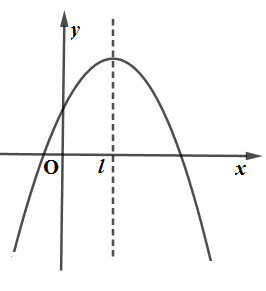 14. 已知函数 的图象与函数 的图象恰好有四个交点,则 的取值范围是.15. 已知二次函数y=x2+bx+c.当-1≤x≤1时,y的取值范围是-1≤y≤1,该二次函数的对称轴为x=m,则m的值是.16. 如图所示,从高为2m的点 处向右上抛一个小球 ,小球路线呈抛物线 形状,小球水平经过2m时达到最大高度6m,然后落在下方台阶B处弹起,已知 m, m, m,若小球弹起形成一条与 形状相同的抛物线,且落点 与 , 在同一直线上,则小球弹起时的最大高度是m
14. 已知函数 的图象与函数 的图象恰好有四个交点,则 的取值范围是.15. 已知二次函数y=x2+bx+c.当-1≤x≤1时,y的取值范围是-1≤y≤1,该二次函数的对称轴为x=m,则m的值是.16. 如图所示,从高为2m的点 处向右上抛一个小球 ,小球路线呈抛物线 形状,小球水平经过2m时达到最大高度6m,然后落在下方台阶B处弹起,已知 m, m, m,若小球弹起形成一条与 形状相同的抛物线,且落点 与 , 在同一直线上,则小球弹起时的最大高度是m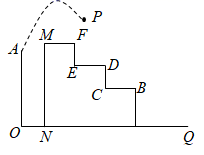
三、作图题(共9分)
-
17. 已知二次函数 的图象经过点 .
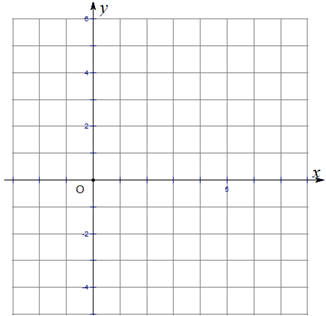 (1)、求这个二次函数的表达式;(2)、画出这个函数的图象,并利用图象解决下列问题:
(1)、求这个二次函数的表达式;(2)、画出这个函数的图象,并利用图象解决下列问题:①直接写出方程 的解;
②当x满足什么条件时, .
四、综合题
-
18. 瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目.某公司生产了一种纪念花灯,每件纪念花灯制造成本为18元.设销售单价x(元),每日销售量y(件)每日的利润w(元).在试销过程中,每日销售量y(件)、每日的利润w(元)与销售单价x(元)之间存在一定的关系,其几组对应量如下表所示:
(元)
19
20
21
30
(件)
62
60
58
40
(1)、根据表中数据的规律,分别写出每日销售量y(件),每日的利润w(元)关于销售单价x(元)之间的函数表达式.(利润=(销售单价-成本单价)×销售件数).(2)、当销售单价为多少元时,公司每日能够获得最大利润?最大利润是多少?(3)、根据物价局规定,这种纪念品的销售单价不得高于32元,如果公司要获得每日不低于350元的利润,那么制造这种纪念花灯每日的最低制造成本需要多少元?19. 如图,已知抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,与y轴交于点C,顶点为P.(提示:若x1 , x2是一元二次方程ax2+bx+c=0(a≠0)的两个实根,则x1+x2=﹣ ,x1•x2= ) (1)、求m的取值范围;(2)、若OA=3OB,求抛物线的解析式;
(1)、求m的取值范围;(2)、若OA=3OB,求抛物线的解析式;
(3)、在(2)中抛物线的对称轴PD上,存在点Q使得△BQC的周长最短,试求出点Q的坐标.20. 已知二次函数.(1)、若 , 且函数图象经过 , 两点,求此二次函数的解析式;并根据图象直接写出函数值时自变量x的取值范围;(2)、在(1)的条件下,已知抛物线与x轴交于A,B两点(点A在点B的左侧),将这条抛物线向右平移m()个单位,平移后的抛物线于x轴交于C,D两点(点C在点D的左侧),若B,C是线段的三等分点,求m的值.(3)、已知 , 当 , q(p,q是实数,)时,该函数对应的函数值分别为P,Q.若 , 求证.21. 在平面直角坐标系中,某个函数图象上任意两点的坐标分别为和(其中t为常数且),将的部分沿直线翻折,翻折后的图象记为;将的部分沿直线翻折,翻折后的图象记为 , 将和及原函数图象剩余的部分组成新的图象G.例如:如图,当时,原函数 , 图象G所对应的函数关系式为.
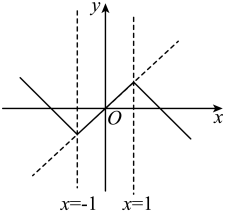 (1)、当时,原函数为 , 图象G与坐标轴的交点坐标是.(2)、对应函数(n为常数).
(1)、当时,原函数为 , 图象G与坐标轴的交点坐标是.(2)、对应函数(n为常数).①时,若图象G与直线恰好有两个交点,求t的取值范围.
②当时,若图象G在上的函数值y随x的增大而减小,直接写出n的取值范围.
22. 如图1,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,过点C作轴,与抛物线交于另一点D,直线与相交于点M.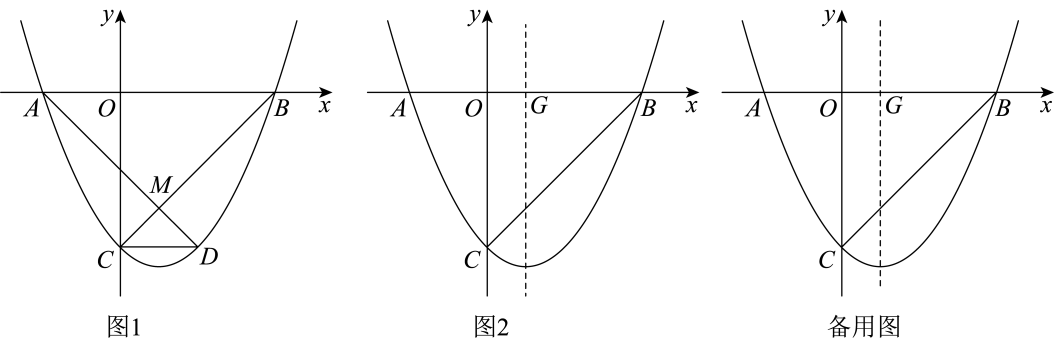 (1)、已知点C的坐标是 , 点B的坐标是 , 求此抛物线的解析式;(2)、若 , 求证:;(3)、如图2,设第(1)题中抛物线的对称轴与x轴交于点G,点P是抛物线上在对称轴右侧部分的一点,点P的横坐标为t,点Q是直线上一点,是否存在这样的点P,使得是以点G为直角顶点的直角三角形,且满足 , 若存在,请直接写出t的值;若不存在,请说明理由.23. 嘉兴某公司抓住“一带一路”的机遇不断创新发展,生产销售某产品.该产品销售量y(万件)与售价x(元/件)之间存在图1(一条线段)所示的变化趋势,总成本P(万元)与销售量y(万件)之间存在图2所示的变化趋势,当时可看成一条线段,当时可看成抛物线.
(1)、已知点C的坐标是 , 点B的坐标是 , 求此抛物线的解析式;(2)、若 , 求证:;(3)、如图2,设第(1)题中抛物线的对称轴与x轴交于点G,点P是抛物线上在对称轴右侧部分的一点,点P的横坐标为t,点Q是直线上一点,是否存在这样的点P,使得是以点G为直角顶点的直角三角形,且满足 , 若存在,请直接写出t的值;若不存在,请说明理由.23. 嘉兴某公司抓住“一带一路”的机遇不断创新发展,生产销售某产品.该产品销售量y(万件)与售价x(元/件)之间存在图1(一条线段)所示的变化趋势,总成本P(万元)与销售量y(万件)之间存在图2所示的变化趋势,当时可看成一条线段,当时可看成抛物线.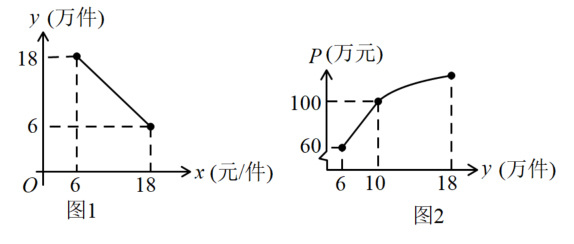 (1)、写出y与x之间的函数关系式;(2)、若销售量不超过10万件时,利润为45万元.求此时的售价为多少元/件?(3)、当售价为多少元时,利润最大,最大值是多少万元?(利润=销售总额-总成本)24. 某水产养殖户,一次性收购了小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养天的总成本为万元;放养天的总成本为万元(总成本=放养总费用+收购成本).(1)、设每天的放养费用是a万元,收购成本为b万元,求a和b的值;(2)、设这批小龙虾放养t天后的质量为m(),销售单价为y元/.根据以往经验可知:m与t的函数关系式为 , y与t的函数关系如图所示
(1)、写出y与x之间的函数关系式;(2)、若销售量不超过10万件时,利润为45万元.求此时的售价为多少元/件?(3)、当售价为多少元时,利润最大,最大值是多少万元?(利润=销售总额-总成本)24. 某水产养殖户,一次性收购了小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养天的总成本为万元;放养天的总成本为万元(总成本=放养总费用+收购成本).(1)、设每天的放养费用是a万元,收购成本为b万元,求a和b的值;(2)、设这批小龙虾放养t天后的质量为m(),销售单价为y元/.根据以往经验可知:m与t的函数关系式为 , y与t的函数关系如图所示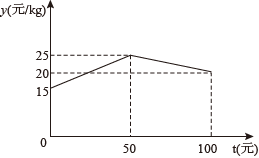
①求y与t的函数关系式;
②设将这批小龙虾放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出W的最大值.(利润=销售总额-总成本)
25. 阅读材料:一般地,对于某个函数,如果自变量x在取值范围内任取x=a与x=时,函数值相等,那么这个函数是“对称函数”.例如,y=x2 , 在实数范围内任取x=a时,y=a2;当x=时,y== a2 , 所以y=x2是“对称函数”.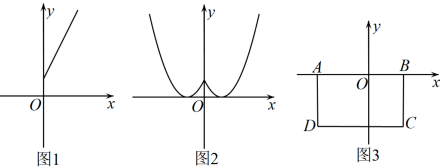 (1)、函数对称函数(填“是”或“不是”).当x≥0时,的图象如图1所示,请在图1中画出x<0时,的图象.(2)、函数的图象如图2所示,当它与直线y=-x+n恰有3个交点时,求n的值.(3)、如图3,在平面直角坐标系中,矩形ABCD的顶点坐标分别是A(-3,0),B(2,0),C(2,-3),D(-3,-3),当二次函数(b>0)的图象与矩形的边恰有4个交点时,求b的取值范围.
(1)、函数对称函数(填“是”或“不是”).当x≥0时,的图象如图1所示,请在图1中画出x<0时,的图象.(2)、函数的图象如图2所示,当它与直线y=-x+n恰有3个交点时,求n的值.(3)、如图3,在平面直角坐标系中,矩形ABCD的顶点坐标分别是A(-3,0),B(2,0),C(2,-3),D(-3,-3),当二次函数(b>0)的图象与矩形的边恰有4个交点时,求b的取值范围.
-