2023年浙教版数学八年级上册第一章三角形的初步认识单元测试（提高版）

试卷更新日期：2023-06-18 类型：单元试卷

进入出卷网下载

一、单选题（每题2分，共20分）

1. 如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE中点，且△ABC的面积等于4cm² ，则阴影部分图形面积等于（）.

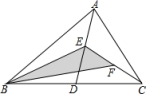A、1cm² B、2cm² C、0.5cm² D、1.5cm²

查看试题解析
2. 五条长度均为整数厘米的线段：a₁ ， a₂ ， a₃ ， a₄ ， a₅ ，满足a₁＜a₂＜a₃＜a₄＜a₅ ，其中a₁＝1厘米，a₅＝9厘米，且这五条线段中的任意三条都不能构成三角形，则a₃＝（）

A、3厘米 B、4厘米 C、3或4厘米 D、不能确定

查看试题解析
3. 下列说法正确的是（）

A、有两边及一边的对角分别相等的两个三角形全等 B、有两边相等的两个直角三角形全等 C、有两个角及第三个角的对边分别相等的两个三角形全等 D、有两个角及一边相等的两个三角形全等

查看试题解析
4. 下列说法不正确的是（）

A、如果两个图形全等，那么它们的形状和大小一定相同； B、面积相等的两个图形是全等图形； C、图形全等，只与形状、大小有关，而与它们的位置无关； D、全等三角形的对应边相等，对应角相等；

查看试题解析
5. 如图，已知在正方形 $A B C D$ 中， $A B = B C = C D = A D = 10$ 厘米， $∠ A = ∠ B = ∠ C = ∠ D = 9 0^{°}$ ，点E在边 $A B$ 上，且 $A E = 4$ 厘米，如果点P在线段BC上以2厘米／秒的速度由B点向C点运动，同时，点Q在线段 $C D$ 上由C点向D点运动，设运动时间为t秒，当ΔBPE与ΔCQP全等时，t的值为（　　）

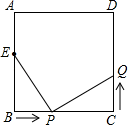A、2 B、2或1.5 C、2.5 D、2.5或2

查看试题解析
6. 如图，在已知的△ABC中，按以下步骤作图：①分别以B、C为圆心，以大于 $\frac{1}{2}$ BC的长为半径作弧，两弧相交于点M、N；②作直线MN交AB于点D ，连接CD ，若CD＝AD ， ∠B＝20°，则下列结论中不正确是（）

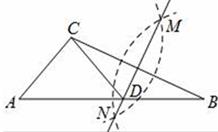A、∠CAD＝40° B、∠ACD＝70° C、点D为△ABC的外心 D、∠ACB＝90°

查看试题解析
7. 如图， $△ A B C$ 的角平分线 $B D$ ， $C E$ 交于点 $P$ ， $∠ A = 60 °$ ， $△ A B C$ 的面积为16，四边形 $A E P D$ 的面积为5，则 $△ B P C$ 的面积为（）

A、5 B、5.5 C、6 D、7

查看试题解析
8. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF $∥$ BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：①∠BOC＝90° $+ \frac{1}{2}$ ∠A，②∠EBO $= \frac{1}{2}$ ∠AEF，③∠DOC+∠OCB＝90°，④设OD＝m，AE+AF＝n，则S_△AEF $= \frac{m n}{2}$ ．其中正确的结论有（）

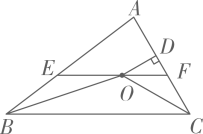A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，在等腰△ABC中，点D，E分别在腰AB，AC上，添加下列条件中的一个，不能判定△ABE≌△ACD的是（）

A、AD=AE B、∠DCB=∠EBC C、∠ADC=∠AEB D、BE=CD

查看试题解析
10. 如图，在Rt $△ A E B$ 和Rt $△ A F C$ 中， $∠ E = ∠ F = 90 °$ ， $B E = C F$ ， BE与AC相交于点M，与CF相交于点D，AB与CF相交于点N， $∠ E A C = ∠ F A B$ ．有下列结论：① $∠ B = ∠ C$ ；② $E D = F D$ ；③ $A C = B E$ ；④ $△ A C N$ ≌ $△ A B M$ ．其中正确结论的个数是（）．

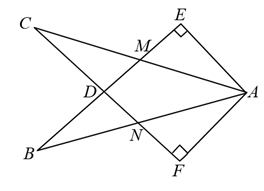A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每空2分，共12分）

11. 已知一个包装盒的底面是内角和为720°的多边形，它是由另一个多边形纸片剪掉一个角以后得到的，则原多边形是边形．

查看试题解析
12. 若三角形的周长为13，且三边均为整数，则满足条件的三角形有种．

查看试题解析
13. 如图，在△ABC中，AB＝AC＝24厘米，∠B=∠C ，BC＝16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为厘米/秒时，能够在某一时刻使△BPD与△CQP全等．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A C = B C$ ，以点A为圆心，任意长为半径画弧，分别交AB、AC于点M、N，再分别以点M、N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，若 $∠ C = 36 °$ ，则 $∠ A D B$ 的度数是．

查看试题解析
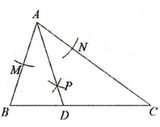15. 如图，在 $△ A B C$ 中，根据尺规作图痕迹，下列四个结论中：① $A F = B F$ ；② $∠ A F D + ∠ F B C = 90 °$ ；③ $D F ⊥ A B$ ；④ $∠ B A F = ∠ C A F$ ．所有正确结论的序号是：．

查看试题解析
16. 如图，点D是等腰 $R t △ A B C$ 的边BC上的一点，过点B作 $B E ⊥ A D$ 于点E，连接CE，若 $A E = 2$ ，则 $S_{△ A E C}$ 的值是．

查看试题解析

三、作图题（共12分）

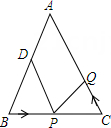
17. 如图，已知甲工厂靠近公路a，乙工厂靠近公路b，为了发展经济，甲、乙两工厂准备合建一个仓库，经协商，仓库必须满足以下两个要求：
①到两工厂的距离相等；
②在 $∠ M O N$ 内，且到两条公路的距离相等．
你能帮忙确定仓库的位置吗？（保留作图痕迹，不写作法）

查看试题解析
18. 如图，在11×7的长方形网格中，每个小正方形的边长均为1，小正方形的每一个顶点叫做格点，线段DE和三角形ABC的顶点都在格点上.根据下列条件，利用网格点和无刻度的直尺画图并解答相关的问题（保留画图痕迹）：

⑴△ABC的面积为 ▲；

⑵在DE的右侧找一点F，使得△DEF与△ABC全等；

⑶画△ABC中BC边上的高AH.

查看试题解析

四、解答题（共76分）

19. 如图，已知四边形 $A B C D$ ，在E在 $C D$ 的延长线上，连接 $B E$ 交 $A D$ 于点F，连结 $B D$ ，已知 $∠ A B D = ∠ E B C ， ∠ A B E = ∠ A D B$ ．

(1)、试判断 $A D$ 与 $B C$ 的位置关系，并说明理由．

(2)、若 $A B ∥ C D$ ， BD平分 $∠ C B E ， ∠ C = ∠ D F E$ ，求 $∠ C$ 的度数．

查看试题解析
20. 如图，已知 $△ A B C$ 的面积是 $60$ ，请完成下列问题：

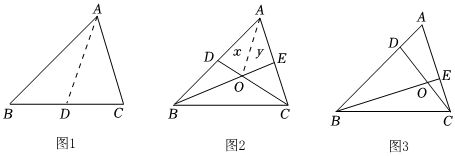(1)、如图 $1$ ， $△ A B C$ 中，若 $A D$ 是 $B C$ 边上的中线，则 $△ A B D$ 的面积 $△ A C D$ 的面积 $($ 填“ $>$ ”、“ $<$ ”或“ $=$ ” $)$ ；

(2)、如图 $2$ ，若 $C D$ 、 $B E$ 分别是 $△ A B C$ 的 $A B$ 、 $A C$ 边上的中线，求四边形 $A D O E$ 的面积可以用如下方法：
连接 $A O$ ，由 $A D = D B$ 得 $S_{△ A D O} = S_{△ B D O}$ ，
同理，可得 $S_{△ C E O} = S_{△ A E O}$ ．
设 $S_{△ A D O} = x$ ， $S_{△ A E O} = y$ ，则 $S_{△ B D O} = x$ ， $S_{△ C E O} = y$ ．
由题意得 $S_{△ A B E} = \frac{1}{2} S_{△ A B C} = 30$ ， $S_{△ A D C} = \frac{1}{2} S_{△ A B C} = 30$ ．
可列方程组 ${\begin{array}{l} 2 x + y = 30 \\ x + 2 y = 30 \end{array}$ ，解得，
通过解这个方程组可得四边形 $A D O E$ 的面积为；

(3)、如图 $3$ ， $A D ： D B = 1 ： 3$ ， $C E ： A E = 2 ： 3$ ，请直接写出四边形 $A D O E$ 的面积 $． ($ 不用书写过程 $)$

查看试题解析
21. 如图，在 $△ A B C$ 中， $B C = 8$ cm， $A G // B C$ ， $A G = 8$ cm，点F从点B出发，沿线段 $B C$ 以4cm/s的速度连续做往返运动，点E从点A出发沿线段 $A G$ 以2cm/s的速度运动至点G，E、F两点同时出发，当点E到达点G时，E、F两点同时停止运动， $E F$ 与 $A C$ 交于点D，设点E的运动时间为t（秒）

(1)、分别写出当 $0 < t < 2$ 和 $2 < t < 4$ 时线段 $B F$ 的长度（用含t的代数式表示）

(2)、当 $B F = A E$ 时，求t的值；

(3)、当 $△ A D E ≌ △ C D F$ 时，直接写出所有满足条件的 $t$ 值.

查看试题解析
22. 【问题呈现】如图①，△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点．求证：∠P＝ $\frac{1}{2}$ ∠A．

(1)、证明：∵BP、CP分别是∠ABC和∠ACD的角平分线，
∴∠PBC＝ $\frac{1}{2}$ ∠ABC，∠PCD＝ $\frac{1}{2}$   ▲   ，
∵∠PCD＝  ▲  ＋∠P，
∴∠P＝∠PCD﹣  ▲   ，
＝ $\frac{1}{2}$ （∠ACD﹣∠ABC
＝ $\frac{1}{2}$   ▲   ．

(2)、【拓展应用】四边形MBCN中，内角∠ABC与外角∠DCE的平分线所在直线相交而成的锐角记为∠P，设∠A＋∠D＝α．
如图②，若α＝225°，求∠P的度数．

(3)、若α＜180°，请利用图③画图探索，则∠P的大小为度．（用含α的代数式表示）

查看试题解析
23. 如图在 $△ A B C$ 和 $△ A D E$ 中， $A B = A C$ ， $A D = A E$ ， $∠ B A C = ∠ D A E =90 °$ ．

(1)、当点D在AC上时，如图（1），求证： $B D = C E$ ．

(2)、将图（1）中的 $△ A D E$ 绕点A顺时针旋转 $α$ 角（ $0 ° < α <90 °$ ），如图（2），线段BD、CE仍相等吗？请说明理由．

(3)、在图（2）中线段BD、CE有怎样的位置关系？请说明理由．

查看试题解析
24. 如图，AB⊥BC，射线CM⊥BC，且BC=4，点P是线段BC（不与点B、C重合）上的动点，过点P作DP⊥AP交射线CM于点D，连接AD．

(1)、如图1，若AB=1，BP=3，求CD的长．

(2)、如图2，若DP平分∠ADC，
①试猜测PB和PC的数量关系，并说明理由；

②若△ADP的面积为5，求四边形ABCD的面积．

(3)、如图3，已知点E是网格中的格点，若三角形ADE是以AD为底边的等腰三角形，那么这样的E点共有个．

查看试题解析
25. 【概念认识】
如图①，在∠ABC中，若∠ABD＝∠DBE＝∠EBC，则BD，BE叫做∠ABC的“三分线”．其中，BD是“邻AB三分线”，BE是“邻BC三分线”．

(1)、【问题解决】
如图②，在△ABC中，∠A＝80°，∠B＝45°，若∠B的三分线BD交AC于点D，求∠BDC的度数；

(2)、如图③，在△ABC中，BP、CP分别是∠ABC邻BC三分线和∠ACB邻BC三分线，且∠BPC＝140°，求∠A的度数；

(3)、【延伸推广】
在△ABC中，∠ACD是△ABC的外角，∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P．若∠A＝m°（m＞54），∠B＝54°，直接写出∠BPC的度数．（用含m的代数式表示）

查看试题解析
26.

(1)、【问题情境】课外兴趣小组活动时，老师提出了如下问题：如图1，在△ABC中，若AB＝13，AC＝9，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE＝AD，连接BE，容易证得△ADC≌△EDB，再由“三角形的三边关系”可求得AD的取值范围是．

解后反思：题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．

(2)、【初步运用】如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且∠FAE＝∠AFE．若AE＝4，EC＝3，求线段BF的长．

(3)、【拓展提升】如图3，在△ABC中，D为BC的中点，DE⊥DF分别交AB，AC于点E，F．求证：BE+CF＞EF．

查看试题解析

2023年浙教版数学八年级上册第一章 三角形的初步认识 单元测试（提高版）

一、单选题（每题2分，共20分）

二、填空题（每空2分，共12分）

三、作图题（共12分）

四、解答题（共76分）

2023年浙教版数学八年级上册第一章三角形的初步认识单元测试（提高版）