2023年浙教版数学八年级上册第一章 三角形的初步认识 章末检测（基础版）
试卷更新日期：2023-06-18 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 在中，已知 ， 则三角形的形状是（ ）A、钝角三角形 B、直角三角形 C、锐角三角形 D、无法确定2. 下列长度的三条线段能组成三角形的是（ ）A、2，3，6 B、5，8，13 C、4，4，7 D、3，4，83. 下列命题中，假命题是（ ）A、全等三角形对应角相等 B、对顶角相等 C、同位角相等 D、有两边对应相等的直角三角形全等4. 观察下列图案，其中与如图全等的是（ ）
A、
B、
C、
D、
5. 下列各组图形中，属全等图形的是（ ）A、周长相等的两个等腰三角形 B、面积相等的两个长方形 C、面积相等的两个直角三角形 D、周长相等的两个圆6. 如图， ， 过点作 ， 垂足为 ， 若 ， 则的度数为（ ）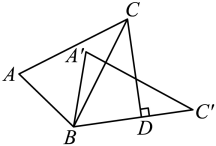
A、 B、 C、 D、7. 下列选项中的尺规作图（各图中的点P都在△ABC的边上），能推出PA＝PC的是（ ）A、
B、
C、
D、
8. 如图是用尺规作的平分线的示意图，那么这样作图的依据是（ ）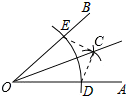
A、SSS B、SAS C、ASA D、AAS9. 如图，有一块三角形的玻璃，不小心掉在地上打成三块，现要到玻璃店重新划一块与原来形状、大小一样的玻璃，只需带到玻璃店（ ）
A、① B、② C、③ D、①、②、③其中任一块10. 如图，点E、F在线段AC上，AF=CE，AD=CB，下列不能推断△ADF≌△CBE是（ ）
A、∠D=∠B B、∠A=∠C C、BE=DF D、AD//BC二、填空题（每空4分，共18分）
-
11. 已知△ABC中，∠A=∠B=∠C，则△ABC是 三角形．12. 将命题“线段垂直平分线上的点到线段两端的距离相等”改写成“如果……，那么……”的形式为 ．13. 如图，若 ， ， ， ， 则的周长为 ．
14. 如图， ， 且∠EAB=120°，∠B=30°，∠CAD=10°，∠CFD=°．
15. 如图，在中，是边上的高，平分 ， 交于点E， ， 若的面积为9，则的长为.
16. 如图，已知 ， 若以“”判定 ， 需添加的条件是
三、作图题（共12分）
-
17. 两个城镇、与两条公路 ， 位置如图所示，其中是东西方向的公路.现电信部门需在处修建一座信号发射塔，要求发射塔到两个城镇、的距离必须相等，到两条公路 ， 的距离也必须相等，且在的内部，请在图中，用尺规作图找出符合条件的点.（不写已知、求作、作法，只保留作图痕迹）
18. 如图，已知.
(1)、尺规作出角平分线；(2)、尺规作中线；(3)、作边的高线.四、解答题（共60分）
-
19. 如图，在ABC中，AD是ABC的高，AE、BF是ABC角平分线，AE与BF相交于点O，∠BOA＝125°，求∠DAC的度数．
20. 如图，△ABE≌△DCE，点A，C，B在一条直线上，∠AED和∠BEC相等吗？为什么？
21. 如图，点D，E分别在AB，AC上，DE∥BC，F是AD上一点，FE的延长线交BC的延长线于点G.求证：
(1)、∠EGH>∠ADE；(2)、∠EGH＝∠ADE＋∠A＋∠AEF.22. 如图，点A，O，B在同一直线上，且 ． 证明：
(1)、点C，O，D在同一直线上；(2)、 ．23. 如图，在中， ， 是的平分线，于E.
(1)、求证：；(2)、若 ， 求的周长.24. 如图，已知AB＝DC，AB∥CD，E、F是AC上两点，且AE＝CF．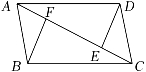
(1)、求证：△ABF≌△CDE；(2)、若∠BCF＝30°，∠CBF＝72°，求∠CED的度数．25. 探究问题：已知∠ABC ， 画一个角∠DEF ， 使DE∥AB ， EF∥BC ， 且DE交BC于点P ． ∠ABC与∠DEF有怎样的数量关系？
(1)、我们发现∠ABC与∠DEF有两种位置关系：如图1与图2所示．①图1中∠ABC与∠DEF数量关系为；图2中∠ABC与∠DEF数量关系为；
请选择其中一种情况说明理由．
②由①得出一个真命题（用文字叙述）： ．
(2)、应用②中的真命题，解决以下问题：若两个角的两边互相平行，且一个角比另一个角的2倍少30°，请直接写出这两个角的度数．