2023年浙教版数学八年级上册1.5.4全等三角形的判定——AAS 同步测试
试卷更新日期:2023-06-18 类型:同步测试
一、单选题
-
1. 如图,是中的平分线,交于点 , 交于点 , 若 , , , 则的长为( )
 A、 B、4 C、5 D、62. 如图,在中, , 以点A为圆心,适当长为半径画弧,分别交、于点D,E,再分别以点D、E为圆心,大于为半径画弧,两弧交于点F,作射线交边于点G,若 , , 则的面积是( )
A、 B、4 C、5 D、62. 如图,在中, , 以点A为圆心,适当长为半径画弧,分别交、于点D,E,再分别以点D、E为圆心,大于为半径画弧,两弧交于点F,作射线交边于点G,若 , , 则的面积是( ) A、2 B、3 C、4 D、53. 如图.点P是的角平分线上的一点,于点E,已知 , 则点P到的距离是( )
A、2 B、3 C、4 D、53. 如图.点P是的角平分线上的一点,于点E,已知 , 则点P到的距离是( ) A、18 B、12 C、6 D、94. 如图,中, , 平分交于点P,若 , , 则的面积是( )
A、18 B、12 C、6 D、94. 如图,中, , 平分交于点P,若 , , 则的面积是( ) A、 B、 C、 D、5. 如图, , , , 则不正确的结论是( )
A、 B、 C、 D、5. 如图, , , , 则不正确的结论是( ) A、与互为余角 B、 C、≌ D、6. 如图,在△ABC中,点D为BC的中点,△AEF的边EF过点C,且AE=EF,AB∥EF,AD平分∠BAE,CE=3,AB=13,则CF=( )
A、与互为余角 B、 C、≌ D、6. 如图,在△ABC中,点D为BC的中点,△AEF的边EF过点C,且AE=EF,AB∥EF,AD平分∠BAE,CE=3,AB=13,则CF=( ) A、10 B、8 C、7 D、67. 如图,A在上,F在上,且 , , 则的长等于( )
A、10 B、8 C、7 D、67. 如图,A在上,F在上,且 , , 则的长等于( ) A、 B、 C、 D、8. 如图,已知 , , 过点A,且 , , 垂足分别为点D,E, , , 则的长为( )
A、 B、 C、 D、8. 如图,已知 , , 过点A,且 , , 垂足分别为点D,E, , , 则的长为( ) A、10 B、8 C、4 D、2
A、10 B、8 C、4 D、2二、填空题
-
9. 如图,射线是的角平分线,是射线上一点,于点 , , 若点是射线上一点, , 则的面积是.
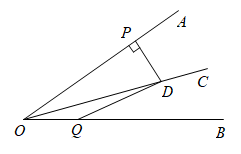 10. 如图,在四边形中, , , , , 则点到边的距离等于 .
10. 如图,在四边形中, , , , , 则点到边的距离等于 . 11. 如图,点D,E分别在线段上,与相交于O点,已知 , 添加一个条件能直接用“”判定 , 符合要求的条件是 .
11. 如图,点D,E分别在线段上,与相交于O点,已知 , 添加一个条件能直接用“”判定 , 符合要求的条件是 . 12. 如图,小虎用10块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板( , ),点C在上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 .
12. 如图,小虎用10块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板( , ),点C在上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 .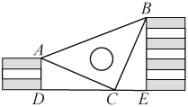
三、综合题
-
13. 如图,∠ACB=90°,BD平分∠ABC交AC于D,DE⊥AB于E,ED的延长线交BC的延长线于F. 求证:AE=CF.
 14. 如图, , 点B为线段上一点,连接 交于点 H,过点A作分别交 , 于点G、点 E. . 求证: .
14. 如图, , 点B为线段上一点,连接 交于点 H,过点A作分别交 , 于点G、点 E. . 求证: . 15. 如图,在△ABC中,D是AB上一点,CF//AB,DF交AC于点E,.
15. 如图,在△ABC中,D是AB上一点,CF//AB,DF交AC于点E,. (1)、求证:(2)、若 , , 求BD的长.16. 如图,在中, , , 点是上一点,连结设: , 当分别满足下列条件时,求的值.
(1)、求证:(2)、若 , , 求BD的长.16. 如图,在中, , , 点是上一点,连结设: , 当分别满足下列条件时,求的值. (1)、AD为边上的中线;(2)、AD为的平分线.
(1)、AD为边上的中线;(2)、AD为的平分线.

