2023年浙教版数学八年级上册1.5.3 全等三角形的判定——ASA 同步测试
试卷更新日期:2023-06-18 类型:同步测试
一、单选题
-
1. 如图,将两块大小相同的三角板(∠B=∠C=30°的直角三角形)按图中所示的位置摆放.若BE交CF于点D交AC于点M,AB交CF于点N,则下列结论:①∠EAM=∠FAN;②△ACN≌△ABM;③∠EAF+∠BAC=120°;④EM=FN;⑤CF⊥BE中,正确的结论有( )
 A、5个 B、4个 C、3个 D、2个2. 如图,点、在上, , , , , , 则的长为( )
A、5个 B、4个 C、3个 D、2个2. 如图,点、在上, , , , , , 则的长为( ) A、4 B、 C、3 D、3. 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为( )
A、4 B、 C、3 D、3. 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为( ) A、2 B、4 C、4.5 D、34. 如图,AD平分∠BAC,AB=AC,连接BD,CD并延长交AC,AB于E,F点,则此图中全等三角形共有( )
A、2 B、4 C、4.5 D、34. 如图,AD平分∠BAC,AB=AC,连接BD,CD并延长交AC,AB于E,F点,则此图中全等三角形共有( )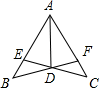 A、2对 B、3对 C、4对 D、5对5. 如图,在中,于点 , 与点 , 与交于点 , 若 , , 则的长为( )
A、2对 B、3对 C、4对 D、5对5. 如图,在中,于点 , 与点 , 与交于点 , 若 , , 则的长为( ) A、3 B、3.5 C、2.5 D、26. 如图,一块三角形的玻璃打碎成四块,现要到玻璃店去配一块完全一样的玻璃,最简单的办法是( )
A、3 B、3.5 C、2.5 D、26. 如图,一块三角形的玻璃打碎成四块,现要到玻璃店去配一块完全一样的玻璃,最简单的办法是( ) A、只带①去 B、带②③去 C、只带④去 D、带①③去7. 如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为点N,∠ACB的平分线垂直于 AD,垂足为M,若BC=7,则DE的长是( )
A、只带①去 B、带②③去 C、只带④去 D、带①③去7. 如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为点N,∠ACB的平分线垂直于 AD,垂足为M,若BC=7,则DE的长是( ) A、6 B、4 C、2 D、58. 如图,是的高线,与相交于点 . 若 , 且的面积为12,则的长度为( )
A、6 B、4 C、2 D、58. 如图,是的高线,与相交于点 . 若 , 且的面积为12,则的长度为( )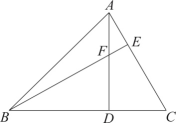 A、4 B、3 C、2 D、1.5
A、4 B、3 C、2 D、1.5二、填空题
-
9. 如图,已知 , 请你添加一个条件,能运用直接说明≌ , 你添加的条件是不添加任何字母和辅助线
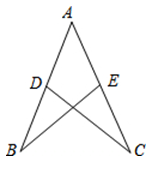 10. 如图,已知 AB//CF,E为DF的中点,若AB=13cm,CF=7cm,则BD=cm .
10. 如图,已知 AB//CF,E为DF的中点,若AB=13cm,CF=7cm,则BD=cm . 11. 如图,D为内一点,平分 , , 垂足为D,交与点E, . 若 , , 则的长为 .
11. 如图,D为内一点,平分 , , 垂足为D,交与点E, . 若 , , 则的长为 . 12. 如图,在中,H是高和的交点,且 , 已知 , 则的长为 .
12. 如图,在中,H是高和的交点,且 , 已知 , 则的长为 .
三、综合题
-
13. 如图,四边形的对角线与相交于点 , ,
求证: .
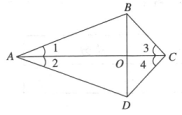 14. 如图,已知在和中,.求证:.
14. 如图,已知在和中,.求证:.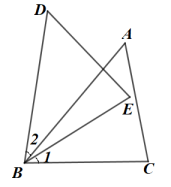 15. 如图,在四边形中,P为边上的一点,.、分别是、的角平分线.
15. 如图,在四边形中,P为边上的一点,.、分别是、的角平分线. (1)、若 , 则的度数为 , 的度数为;(2)、求证:;(3)、设 , , 过点P作一条直线,分别与 , 所在直线交于点E、F,若 , 直接写出的长(用含a的代数式表示)16. 如图,点B,F,C,E在直线l上(点F,C之间不能直接测量),点A,D在l的异侧, , , 测得.
(1)、若 , 则的度数为 , 的度数为;(2)、求证:;(3)、设 , , 过点P作一条直线,分别与 , 所在直线交于点E、F,若 , 直接写出的长(用含a的代数式表示)16. 如图,点B,F,C,E在直线l上(点F,C之间不能直接测量),点A,D在l的异侧, , , 测得.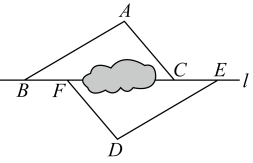 (1)、求证:≌;(2)、若 , , 求的长.
(1)、求证:≌;(2)、若 , , 求的长.

