2023年浙教版数学八年级上册1.3 证明 同步测试
试卷更新日期:2023-06-18 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、过C作EF AB
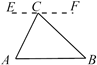 B、过AB上一点D作DE BC,DF AC
B、过AB上一点D作DE BC,DF AC 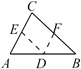 C、延长AC到F,过C作CE AB
C、延长AC到F,过C作CE AB  D、作CD⊥AB于点D
D、作CD⊥AB于点D 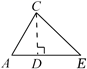 2. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则回答正确的是( )
2. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则回答正确的是( )已知:如图,∠BEC=∠B+∠C,求证:AB∥CD.
证明:延长BE交(※)于点F,则∠BEC=(⊙)+∠C.
又∵∠BEC=∠B+∠C,
∴∠B=(▲)
∴AB∥CD((□)相等,两直线平行)
 A、⊙代表∠FEC B、□代表同位角 C、▲代表∠EFC D、※代表AB3. 图1是一路灯的实物图,图2是该路灯的平面示意图, , , 则图2中的度数为( )
A、⊙代表∠FEC B、□代表同位角 C、▲代表∠EFC D、※代表AB3. 图1是一路灯的实物图,图2是该路灯的平面示意图, , , 则图2中的度数为( ) A、 B、 C、 D、4. 如图,是的一个外角,E是边AB上一点,下列结论错误的是( )
A、 B、 C、 D、4. 如图,是的一个外角,E是边AB上一点,下列结论错误的是( ) A、 B、 C、 D、5. 下列各图中,当a∥b时,符合∠1=∠2+∠3关系的是( )A、
A、 B、 C、 D、5. 下列各图中,当a∥b时,符合∠1=∠2+∠3关系的是( )A、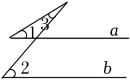 B、
B、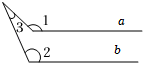 C、
C、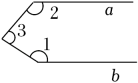 D、
D、 6. 如图,在中, , 是的高线,是的角平分线,则的度数是( )
6. 如图,在中, , 是的高线,是的角平分线,则的度数是( )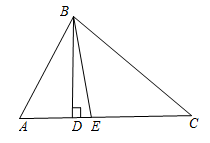 A、 B、 C、 D、7. 如图,是的外角的平分线,若 , , 则( )
A、 B、 C、 D、7. 如图,是的外角的平分线,若 , , 则( ) A、35° B、40° C、45° D、55°8. 如图,在△ABC中,AD是高,AE是角平分线,AF是中线.则下列结论错误的是( )
A、35° B、40° C、45° D、55°8. 如图,在△ABC中,AD是高,AE是角平分线,AF是中线.则下列结论错误的是( ) A、BF=CF B、∠BAF=∠CAF C、∠B+∠BAD=90° D、9. 如图,在△ABC中,∠A=90°,BE,CD分别平分∠ABC和∠ACB,且相交于F, , 于点G,则下列结论 ①∠CEG = 2∠DCA;②CA平分∠BCG;③∠ADC =∠GCD;④∠DFB=∠A;⑤∠DFE=135°,其中正确的结论是( )
A、BF=CF B、∠BAF=∠CAF C、∠B+∠BAD=90° D、9. 如图,在△ABC中,∠A=90°,BE,CD分别平分∠ABC和∠ACB,且相交于F, , 于点G,则下列结论 ①∠CEG = 2∠DCA;②CA平分∠BCG;③∠ADC =∠GCD;④∠DFB=∠A;⑤∠DFE=135°,其中正确的结论是( ) A、①②③ B、①③④ C、①③④⑤ D、①②③④10. 如图,对任意的五角星,结论正确的是( )
A、①②③ B、①③④ C、①③④⑤ D、①②③④10. 如图,对任意的五角星,结论正确的是( )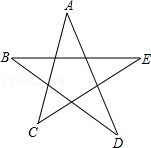 A、∠A+∠B+∠C+∠D+∠E=90° B、∠A+∠B+∠C+∠D+∠E=180° C、∠A+∠B+∠C+∠D+∠E=270° D、∠A+∠B+∠C+∠D+∠E=360°
A、∠A+∠B+∠C+∠D+∠E=90° B、∠A+∠B+∠C+∠D+∠E=180° C、∠A+∠B+∠C+∠D+∠E=270° D、∠A+∠B+∠C+∠D+∠E=360°二、填空题(每空4分,共24分)
-
11. 如图,已知 , 则的度数为.
 12. 如图,在中,平分 , 点在射线上,于 , , , 则的度数为.
12. 如图,在中,平分 , 点在射线上,于 , , , 则的度数为. 13. 在中, , CD平分交AB于D点, , 交BC的延长线于点E,已知 , 则度.
13. 在中, , CD平分交AB于D点, , 交BC的延长线于点E,已知 , 则度. 14. 在你所学过的几何知识中,可以证明两个角相等定理有(写出三个定理即可)15. 如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF;则以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC+∠ABD=90°;其中正确的结论有 .
14. 在你所学过的几何知识中,可以证明两个角相等定理有(写出三个定理即可)15. 如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF;则以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC+∠ABD=90°;其中正确的结论有 . 16. 如图,把一副三角板的两个直角三角形叠放在一起,则α的度数为 .
16. 如图,把一副三角板的两个直角三角形叠放在一起,则α的度数为 .
三、解答题(共8题,共66分)
-
17. 证明命题“三角形三个内角的和等于180°”是真命题.
已知:
求证:
证明:
18. 把下面的证明过程补充完整:已知:如图, , .

求证: .
证明:∵(已知),
∴ ▲ ( ),
∴( ),
∵( ),
∴ ▲ ( ),
∴( ),
∴( ).
19. 叙述并证明三角形内角和定理.20. 如图, , 求证: , 请完成证明过程及理由填写.
证明:(已知),
( )
(等量代换).
▲ ( )
▲ ( )
( ),
( )
( )
21. 在探索并证明三角形的内角和定理“三角形三个内角的和等于180°”时,圆圆同学添加的辅助线为“过点A作直线DE // BC”.请写出“已知”、“求证”,并补全证明.已知:
求证:
证明:过点A作直线DE // BC.



