2023年浙教版数学八年级上册1.2 定义与命题 同步测试

试卷更新日期：2023-06-18 类型：同步测试

进入 出卷网 下载

一、单选题（每题3分，共30分）

  • 1. 下列语句是命题的是（    ）
    A、作直线AB的垂线 B、在线段AB上取点C C、垂线段最短吗？ D、同旁内角互补

    查看试题解析

  • 2. 下列命题是假命题的是（    ）
    A、无理数都是无限小数 B、−1 的立方根是它本身 C、三角形内角和都是180° D、内错角相等

    查看试题解析

  • 3. 下列命题中，真命题是（  ）
    A、两个角的和等于平角时，这两个角互为邻补角 B、已知直线b//c ， a→⊥b→ ， 则a⊥c C、相等的角是对顶角 D、同旁内角互补

    查看试题解析

  • 4. 下列语句不是命题的是 （     ）
    A、x与y的和等于x+y吗？ B、不平行的两条直线只有一个交点    C、两点之间线段最短 D、相等的角是对顶角

    查看试题解析

  • 5. 下列命题是真命题的是（    ）
    A、过一点有且只有一条直线和已知直线平行 B、a2=b2 ， 则a=b C、a与b互为相反数，则b3与a3互为相反数 D、643的平方根是2

    查看试题解析

  • 6. 下列句子是命题的是（   ）
    A、画∠AOB=30° B、小于直角的角是锐角吗？      C、连结CD D、若a+b=c+b ， 则a=c

    查看试题解析

  • 7. 下列语句中，不是命题的是（  ）
    A、直角都等于90∘ B、对顶角相等 C、互补的两个角不相等 D、作线段AB

    查看试题解析

  • 8. 下列叙述错误的是（ ）
    A、所有的命题都有条件和结论 B、所有的命题都是定理 C、所有的定理都是命题 D、所有的公理都是真命题

    查看试题解析

  • 9. 下列命题是真命题的是（    ）
    A、若a=b ， 则a2=b2 B、若|a|=|b| ， 则a=b C、若ab=0 ， 则a=0 D、若a2=b2 ， 则a=b

    查看试题解析

  • 10. 若取一个x的值，能说明命题“若x>−6 ， 则x2>36”是假命题，则x的值可以取（    ）
    A、−8 B、8 C、7 D、5

    查看试题解析

二、填空题（每空4分，32分）

  • 11. 命题“同旁内角互补，两直线平行”写成“如果……那么……”的形式是它是命题（填“真”或“假”）.

    查看试题解析

  • 12. 把“对顶角相等”改写成“如果……那么……”的形式 ．

    查看试题解析

  • 13. 把命题“同位角相等”改写成“如果……那么……”的形式为 ．

    查看试题解析

  • 14. 能说明命题：“若两个角α ， β互补，则这两个角必为一个锐角一个钝角”是假命题的反例是.

    查看试题解析

  • 15. 把定理“有两个角互余的三角形是直角三角形”，写成“如果...那么...”的形式是：如果 ， 那么 ．

    查看试题解析

  • 16. 如图，现有以下3个论断：①AB∥CD；②∠B=∠C；③∠E=∠F ． 如果以其中2个论断为条件，另一个论断为结论构造命题，能够构成个真命题．

    查看试题解析

三、解答题（共7题，共66分）

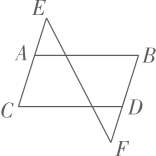
  • 17. “定义、定理、基本事实、命题、真命题、假命题”它们之间的关系恰好可以用下图表示，请指出A，B，C，D，E，F分别与它们中的哪一个对应．

    查看试题解析

  • 18. 指出下列命题的条件和结论，并改写成“如果……那么……”的形式：
    (1)、对顶角相等；
    (2)、同角的余角相等；
    (3)、三角形的内角和等于180°；
    (4)、角平分线上的点到角的两边距离相等．

    查看试题解析

  • 19. 下列各命题的条件是什么？结论是什么？
    (1)、两直线平行，同位角相等；
    (2)、过一点有且只有一条直线与已知直线平行．

    查看试题解析

  • 20. 试用举反例的方法说明下列命题是假命题．

    例如：如果ab<0，那么a+b<0．

    反例：设a=4，b=-3，ab=4´（-3）=-12<0，而a+b=4+（-3）=1>0，所以这个命题是假命题．

    (1)、如果a+b>0，那么ab>0．
    (2)、如果a是无理数，b也是无理数，那么a+b也是无理数．

    查看试题解析

  • 21. 判断下面命题的真假，若是假命题，请举出反例说明:

    ①一个三角形的3个内角中至少有1个钝角；

    ②若三条线段a ， b ， c满足a+b>c ， 则这三条线段a ， b ， c能够组成三角形；

    ③个位数字是5的整数，能被5整除；

    ④对于所有的自然数n ， 代数式n2-n+11的值都是质数；

    查看试题解析

  • 22. 如图，有三个条件：①∠1=∠2 ， ②∠C=∠D ， ③∠A=∠F ， 从中任选两个作为已知条件，另一个作为结论，可以组成3个命题，例如：

    以③作为结论的命题是：如图，已知∠1=∠2 ， ∠C=∠D ， 求证：∠A=∠F

    (1)、请按要求写出命题：

    以①作为结论的命题是：；

    以②作为结论的命题是：；

    (2)、请证明以②作为结论的命题．

    查看试题解析

  • 23. 如图，现有以下三个条件：①AB//CD ， ②∠B=∠C ， ③∠E=∠F.请你以其中两个作为题设，另一个作为结论构造命题.

    (1)、你构造的是哪几个命题？
    (2)、你构造的命题是真命题还是假命题？若是真命题，请给予证明；若是假命题，请举出反例（证明其中的一个命题即可）.

    查看试题解析