2023年浙教版数学八年级上册1.1认识三角形 同步测试
试卷更新日期:2023-06-18 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 在中, , 则是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形2. 三角形是指( )A、由三条线段所组成的封闭图形 B、由不在同一直线上的三条直线首尾顺次相接组成的图形 C、由不在同一直线上的三条线段首尾顺次相接组成的图形 D、由三条线段首尾顺次相接组成的图形3. 观察下列图形,其中是三角形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 两根长度分别为2,10的木棒,若想钉一个三角形木架,第三根木棒的长度可以是( )A、13 B、10 C、7 D、65. 能把一个三角形的面积分成相等的两部分的线是这个三角形的( )A、一条高 B、一条中线 C、一条角平分线 D、一边上的中垂线6. 如图,D、E分别是BC、AC的中点, , 则的面积为( )
4. 两根长度分别为2,10的木棒,若想钉一个三角形木架,第三根木棒的长度可以是( )A、13 B、10 C、7 D、65. 能把一个三角形的面积分成相等的两部分的线是这个三角形的( )A、一条高 B、一条中线 C、一条角平分线 D、一边上的中垂线6. 如图,D、E分别是BC、AC的中点, , 则的面积为( ) A、4 B、8 C、10 D、127. 若三角形三个内角度数比为 , 则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定8. 如图,在△ABC中,∠C=90°,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )A、
A、4 B、8 C、10 D、127. 若三角形三个内角度数比为 , 则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定8. 如图,在△ABC中,∠C=90°,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )A、 B、
B、 C、
C、 D、
D、 9. 利用直角三角板,作的高线,下列作法正确的是( )A、
9. 利用直角三角板,作的高线,下列作法正确的是( )A、 B、
B、 C、
C、 D、
D、 10. 用12根等长的火柴棒拼成一个三角形,火柴棒不允许剩余,重叠和折断,则能摆出不同的三角形的个数是( )A、1个 B、2个 C、3个 D、4个
10. 用12根等长的火柴棒拼成一个三角形,火柴棒不允许剩余,重叠和折断,则能摆出不同的三角形的个数是( )A、1个 B、2个 C、3个 D、4个二、填空题(每空3分,共21分)
-
11. 如图,的三条中线AD,BE,CF交于点O,若的面积为20,那么阴影部分的面积之和为.
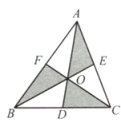 12. 三角形的两边长分别是10和8,则第三边的x取值范围是.13. 若一个三角形三个内角的度数之比为1:2:3,则这个三角形是三角形(填“锐角”、“直角”或“钝角”) .14. 如图, , , 点B在射线上,若为钝角三角形,则线段长的取值范围是.
12. 三角形的两边长分别是10和8,则第三边的x取值范围是.13. 若一个三角形三个内角的度数之比为1:2:3,则这个三角形是三角形(填“锐角”、“直角”或“钝角”) .14. 如图, , , 点B在射线上,若为钝角三角形,则线段长的取值范围是. 15. 如图,以点A为顶点的三角形有个,它们分别是 .
15. 如图,以点A为顶点的三角形有个,它们分别是 . 16. 如图所示,∠ADC=°.
16. 如图所示,∠ADC=°.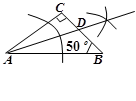
三、作图题(共9分)
-
17. 在如图所示的方格纸中,

⑴在中,作BC边上的高AD.
⑵作AC边上的中线BE.
⑶求的面积.
四、解答题(共8题,共60分)
-
18. 先化简,再求值: , 其中a,2,4为的三边长,且a为整数.19. 如图所示,在中,平分交于点E,交于点D, , , 求的度数.
 20. 如图:已知在△ABC中,AD平分∠BAC,AE⊥BC,垂足为E,∠B=38°,∠C=70°,求∠DAE的度数.
20. 如图:已知在△ABC中,AD平分∠BAC,AE⊥BC,垂足为E,∠B=38°,∠C=70°,求∠DAE的度数.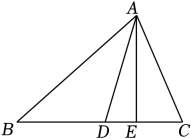 21. 在中, , .(1)、求 , , 的度数;(2)、按边分类,属于三角形,按角分类,属于三角形.22. 在中, , .(1)、若是整数,求的长.(2)、已知是的中线,若的周长为10,求三角形的周长.23. 如图,在四边形中, , 平分 , .
21. 在中, , .(1)、求 , , 的度数;(2)、按边分类,属于三角形,按角分类,属于三角形.22. 在中, , .(1)、若是整数,求的长.(2)、已知是的中线,若的周长为10,求三角形的周长.23. 如图,在四边形中, , 平分 , . (1)、画出的高;(2)、的面积等于 .24. 如图
(1)、画出的高;(2)、的面积等于 .24. 如图 (1)、如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C直角顶点X在△ABC内部,若∠A=30︒,则∠ABC+∠ACB=︒,∠XBC+∠XCB=︒(2)、如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,直角顶点X还在△ABC内部,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.25. 等面积法是一种常用的、重要的数学解题方法.
(1)、如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C直角顶点X在△ABC内部,若∠A=30︒,则∠ABC+∠ACB=︒,∠XBC+∠XCB=︒(2)、如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,直角顶点X还在△ABC内部,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.25. 等面积法是一种常用的、重要的数学解题方法. (1)、如图1,在中, , , , , , 则的长为:.(2)、如图2,在中, , , 则的高与的比是: .(3)、如图3,在中, , 点D,P分别在边 , 上,且 , , , 垂足分别为点E,F.若 , 求的值.
(1)、如图1,在中, , , , , , 则的长为:.(2)、如图2,在中, , , 则的高与的比是: .(3)、如图3,在中, , 点D,P分别在边 , 上,且 , , , 垂足分别为点E,F.若 , 求的值.
-