2023年浙教版数学九年级上册1.4 二次函数的应用同步测试

试卷更新日期：2023-06-18 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 二次函数 $y = k x^{2} - 4 x + 2$ 的图象与 $x$ 轴有两个交点，则 $k$ 满足的条件是（）

A、 $k > 2$ B、 $k = 3$ C、 $k < 2$ 且 $k \neq 0$ D、 $k \leq 2$

查看试题解析
2. 二次函数 $y = x^{2} - 3 x + 1$ 的图象与y轴的交点坐标是（）

A、 $(0 ， 0)$ B、 $(0 ， 1)$ C、 $(0 ， - 3)$ D、 $(3 ， 0)$

查看试题解析
3. 如表是二次函数 $y = a x^{2} + b x - 5$ 的自变量x与函数值y的部分对应值，那么方程 $a x^{2} + b x - 5 = 0$ 的一个根的取值范围是（）
x
…
1
1.1
1.2
1.3
1.4
…
y
…
-1
-0.49
0.04
0.59
1.16
…

A、 $1.1 ∼ 1.2$ B、 $1 ∼ 1.1$ C、 $1.2 ∼ 1.3$ D、 $1.3 ∼ 1.4$

查看试题解析
4. 已知抛物线y＝x²+bx的对称轴为直线x＝3，则关于x的不等式x²+bx＜﹣8的取值范围是（）

A、1＜x＜5 B、2＜x＜4 C、0＜x＜6 D、﹣1＜x＜7

查看试题解析
5. 二次函数 $y = - {(x - b)}^{2} + 4 b + 1$ 图象与一次函数 $y = - x + 5 (- 1 \leq x \leq 5)$ 只有一交点，则 $b$ 的值为（）

A、 $b = 0.75$ B、 $b = 2$ 或 $b = 12$ 或 $b = 0.75$ C、 $2 < b \leq 12$ D、 $2 < b \leq 12$ 或 $b = 0.75$

查看试题解析
6. 用48米木料制作成一个如图所示的“目”形长方形大窗框（横档EF，GH也用木料）．其中AB∥EF∥GH∥CD，要使窗框ABCD的面积最大，则AB的长为（）

A、6米 B、8米 C、12米 D、 $4 \sqrt{3}$ 米

查看试题解析
7. 如图，四边形ABCD中，AB=AD ， CE⊥BD ， CE= $\frac{1}{2}$ BD ．若△ABD的周长为20cm，则△BCD的面积S（cm²）与AB的长x（cm）之间的函数关系式可以是（）

A、 $S = \frac{1}{4} x^{2} - 10 x + 100$ B、 $S = 2 x^{2} - 40 x + 200$ C、 $S = x^{2} - 20 x + 100$ D、 $S = x^{2} + 20 x + 100$

查看试题解析
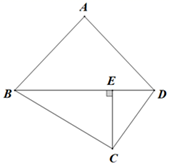8. 将进货单价为30元的某种商品按零售价100元1件卖出时，每天能卖出20件．若这种商品的零售价在一定范围内每降价1元，其日销售量就增加1件，为了获得最大的利润，则应降价（）

A、5元 B、15元 C、25元 D、35元

查看试题解析
9. 将进货价格为35元的商品按单价40元售出时，能卖出200个.已知该商品单价每上涨1元，其销售量就减少5个.设这种商品的售价上涨x元时，获得的利润为y元，则下列关系式正确的是（）

A、y＝（x-35）（200-5x） B、y＝（x+40）（200−10x） C、y＝（x+5）（200-5x） D、y＝（x+5）（200−10x）

查看试题解析
10. 如图，小强在某次投篮中，球的运动路线是抛物线 $y = - \frac{1}{5} x^{2} + 3.5$ 的一部分，若命中篮圈中心，则他与篮筐底的距离 $l$ 是（）

A、3m B、3.5m C、4m D、4.5m

查看试题解析

二、填空题（每空4分，共20分）

11. 写出一个二次函数，满足图象开口向下，顶点在y轴上，且与x轴有两个交点：.

查看试题解析
12. 抛物线 $y = x^{2} - 2 x + 0.5$ 如图所示，利用图象可得方程 $x^{2} - 2 x + 0.5 = 0$ 的近似解为（精确到0.1）.

查看试题解析
13. $y = - 3 x^{2} + b x + c$ 经过点 $A (0 ， 2) ， B (4 ， 2)$ ，则不等式 $- 3 x^{2} + b x + c < 2$ 的解集是．

查看试题解析
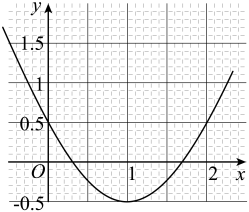14. 如图，将二次函数 $y = - x^{2} + x + 6$ 在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新的函数图象，当直线 $y = - x + m$ 与新图象有4个交点时，m的取值范围是.

查看试题解析
15. 从地面竖直向上跑出一小球，小球的高度 $h$ （单位： $m$ ）与小球的运动时间 $t$ （单位： $s$ ）之间的关系式是 $h = 30 t - 2 t^{2} (0 \leq t \leq 6)$ .小球运动到 $s$ 时，达到最大高度．

查看试题解析

三、解答题（共8题，共70分）

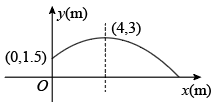
16. 一运动员推铅球，铅球经过的路线为如图所示的抛物线.求铅球的落地点离运动员有多远（结果保留根号）？

查看试题解析
17. 如图，用一段长为30m的篱笆围成一个一边靠墙的矩形菜园，墙长为18m．设矩形 $A B C D$ 的面积为 $S (m^{2})$ ．问 $A B$ 长为多少时S最大，并求最大面积．

查看试题解析
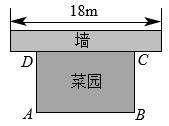18. 已知二次函数y=x²﹣x﹣6.求二次函数的图象与坐标轴的交点所构成的三角形的面积.

查看试题解析
19. 利民商店销售一种进价为50元/件的土特产商品，当售价为60元/件，每周可卖出200件，若每件商品的售价每上涨1元，则每周就会少卖10件．求利民商店将售价上涨多少时每周可获得最大利润？最大利润是多少？

查看试题解析
20. 某超市以每件13元的价格购进一种商品，销售时该商品的销售单价不低于进价且不高于18元．经过市场调查发现，该商品每天的销售量y（件）与销售单价x（元）之间满足如图所示的一次函数关系．

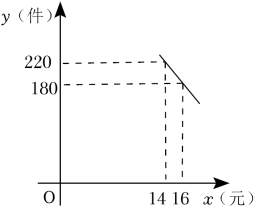(1)、求y与x之间的函数关系式；

(2)、销售单价定为多少时，该超市每天销售这种商品所获的利润最大？最大利润是多少？

查看试题解析
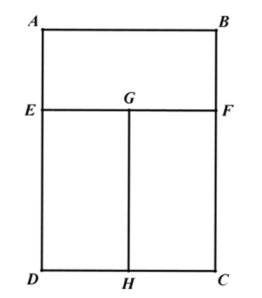21. 用长为8米的铝合金条制成如图窗框，已知矩形 $A E F B$ ，矩形 $E D H G$ ，矩形 $G H C F$ 的面积均相等，设 $A B$ 的长为 $x$ 米.

(1)、请用含 $x$ 的代数式表示 $A D$ 的长.

(2)、设矩形 $A B C D$ 的面积为 $y$ ，出于实际考虑，我们要求窗框的高度( $A D$ )至少为1米，宽度( $A B$ )至少为1.5米，则当 $x$ 取何值时，透光面积 $y$ 最大，并求出面积的最大值.

查看试题解析
22. 如图二次函数 $y ＝ a x^{2} ＋ b x ＋ c$ 的图象与x轴交于点 $(1 ， 0)$ 、 $(3 ， 0)$ ，根据图象解答下列问题：

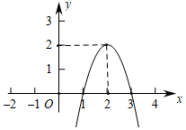(1)、写出方程 $a x^{2} ＋ b x ＋ c ＝ 0$ 的两个根；

(2)、当x为何值时， $y ＞ 0$ ？当x为何值时， $y ＜ 0$ ？

(3)、写出y随x的增大而减小的自变量x的取值范围．

查看试题解析
23. “中国元素”几乎遍布卡塔尔世界杯的每一个角落，某特许商品专卖店销售中国制造的纪念品，深受大家喜爱.自世界杯开赛以来，其销量不断增加，该商品销售第x天（ $1 \leq x \leq 28$ ，且x为整数）与该天销售量y（件）之间满足函数关系如下表所示：
第x天
1
2
3
4
5
6
7
…
销售量y（件）
220
240
260
280
300
320
340
…
为回馈项客，该商家将此纪念品的价格不断下调，其销售单价z（元）与第x天（ $1 \leq x \leq 28$ ，且x为整数）成一次函数关系，当 $x = 1$ 时， $z = 98$ ，当 $x = 2$ 时， $z = 96$ .已知该纪念品成本价为20元/件.

(1)、求y关于x的函数表达式，及z与x之间的函数关系式；

(2)、求这28天中第几天销售利润最大，并求出最大利润；

(3)、商店担心随着世界杯的结束该纪念品的销售情况会不如从前，决定在第20天开始每件商品的单价在原来价格变化的基础上再降价a元销售，销售第x天与该天销售量y（件）仍然满足原来函数关系，问第几天的销售利润取得最大值，若最大利润是20250元，求a的值.

查看试题解析

第x天	1	2	3	4	5	6	7	…
销售量y（件）	220	240	260	280	300	320	340	…

x	…	1	1.1	1.2	1.3	1.4	…
y	…	-1	-0.49	0.04	0.59	1.16	…

2023年浙教版数学九年级上册1.4 二次函数的应用 同步测试

一、单选题（每题3分，共30分）

二、填空题（每空4分，共20分）

三、解答题（共8题，共70分）

2023年浙教版数学九年级上册1.4 二次函数的应用同步测试