2023年浙教版数学九年级上册1.3二次函数的性质同步测试

试卷更新日期：2023-06-18 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 已知点 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ 在二次函数 $y = a x^{2} - 2 a x + b (a > 0)$ 的图像上，若 $y_{1} > y_{2}$ ，则必有（）

A、 $x_{1} > x_{2} > 1$ B、 $x_{1} < x_{2} < 1$ C、 $| x_{1} - 1 | < | x_{2} - 1 |$ D、 $| x_{1} - 1 | > | x_{2} - 1 |$

查看试题解析
2. 二次函数 $y = a x^{2} + 4 x + 1$ （ $a$ 为实数，且 $a < 0$ ），对于满足 $0 \leq x \leq m$ 的任意一个 $x$ 的值，都有 $- 2 ≤ y ≤ 2$ ，则 $m$ 的最大值为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、2 D、 $\frac{3}{2}$

查看试题解析
3. 已知二次函数 $y = a x^{2} - 4 a x + 5 (a > 0)$ ，当 $0 \leq x \leq m$ 时，y有最小值 $- 4 a + 5$ 和最大值5，则m的取值范围为（）

A、 $m \geq 2$ B、 $0 \leq m \leq 2$ C、 $1 \leq m \leq 2$ D、 $2 \leq m \leq 4$

查看试题解析
4. 如图，抛物线y=x²+bx+c (b， c为常数)经过点A (1，0)，点B (0，3)，点P在该抛物线上，其横坐标为m，若该抛物线在点P左侧部分(包括点P)的最低点的纵坐标为2-m．则m的值为（）

A、m=3 B、m= $\frac{3 - \sqrt{5}}{2}$ C、m= $\frac{3 \pm \sqrt{5}}{2}$ D、m=3或m= $\frac{3 - \sqrt{5}}{2}$

查看试题解析
5. 已知二次函数 $y = a x^{2} + b x + c$ 的图像开口向下，顶点坐标为 $(3 ， - 7)$ ，那么该二次函数有（）

A、最小值-7 B、最大值-7 C、最小值3 D、最大值3

查看试题解析
6. 已知二次函数y＝x²+bx+c，当m≤x≤m+1时，此函数最大值与最小值的差（）

A、与m，b，c的值都有关 B、与m，b，c的值都无关 C、与m，b的值都有关，与c的值无关 D、与b，c的值都有关，与m的值无关

查看试题解析
7. 二次函数 $y = a x^{2} + 4 a x + c (a < 0 ， a ， c$ 均为常数 $)$ 的图象经过 $A (- 5 ， y_{1})$ ， $B (- 1 ， y_{2})$ ， $C (0 ， y_{3})$ 三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{2} > y_{1} > y_{3}$ C、 $y_{2} > y_{3} > y_{1}$ D、 $y_{3} > y_{2} > y_{1}$

查看试题解析
8. 二次函数 $y = x^{2} + b x + 1$ 中当 $x > 1$ 时 $y$ 随 $x$ 的增大而增大，则一次项系数 $b$ 满足（）

A、 $b > - 2$ B、 $b \geq - 2$ C、 $b < - 2$ D、 $b = - 2$

查看试题解析
9. 已知二次函数 $y = - x^{2} + 2 m x$ ，对于其图像和性质，下列说法错误的是（）

A、图像开口向下 B、图像经过原点 C、当 $x > 2$ 时，y随x的增大而减小，则 $m < 2$ D、当 $x < m$ 时，y随x的增大而增大

查看试题解析
10. 如图，已知开口向上的抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴交于点 $(- 1 ， 0)$ ，对称轴为直线 $x = 1$ ．下列结论：① $a b c > 0$ ；② $2 a + b = 0$ ；③若关于 $x$ 的方程 $a x^{2} + b x + c + 1 = 0$ 一定有两个不相等的实数根；④ $a > \frac{1}{3}$ .其中正确的个数有（）

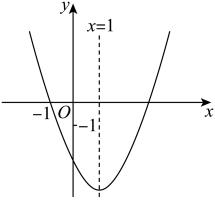A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每空4分，共24分）

11. 当 $a \leq x \leq a + 1$ 时，函数 $y = x^{2} - 2 x + 1$ 的最小值为4，则a的值为.

查看试题解析
12. 对于二次函数 $y = a x^{2} + b x + c$ ， $y$ 与 $x$ 的部分对应值如表所示． $x$ 在某一范围内， $y$ 随 $x$ 的增大而减小，写出一个符合条件的 $x$ 的取值范围．
$x$
…
-1
0
1
2
3
…
$y$
…
-3
1
3
3
1
…

查看试题解析
13. 已知 $A (- 2 ， y_{1})$ ， $B (- 1 ， y_{2})$ ， $C (5 ， y_{3})$ 都在二次函数 $y = - x^{2} + 2 x + k$ 的图象上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 从小到大排序为．

查看试题解析
14. 已知两点 $A (- 6 ， y_{1})$ ， $B (2 ， y_{2})$ 均在抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 上，点 $C (x_{0} ， y_{0})$ 是该抛物线的顶点.若 $y_{0} \geq y_{1} \geq y_{2}$ ，则 $x_{0}$ 的取值范围是.

查看试题解析
15. 二次函数 $y = - x^{2} + 2 x - 4$ ，当 $- 1 \leq x \leq 2$ 时，y的取值范围是.

查看试题解析
16. 已知点 $P (m ， n)$ 在二次函数 $y = x^{2} + 4$ 的图象上，则 $m - n$ 的最大值等于.

查看试题解析

三、解答题（共6题，共66分）

17. 求函数 $y = - x^{2} + 4 x + 5$ 的最值，并说明是最大值还是最小值．

查看试题解析
18. 若点 $A (- 1 ， y_{1})$ ， $B (2 ， y_{2})$ ， $C (3 ， y_{3})$ 在抛物线 $y = - 2 x^{2} + 8 x + c$ 的图象上，请判断 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系，并说明理由.

查看试题解析
19. 已知二次函数 $y = x^{2} + b x + c$ 经过（0， $- 2$ ）和（1， $- 2$ ）．

(1)、求该二次函数的表达式和对称轴.

(2)、当 $- 1 \leq x \leq 3$ 时，求该二次函数的最大值和最小值.

查看试题解析
20. 已知抛物线 $y = a x^{2} + b x (a > 0)$ ．

(1)、若抛物线经过点 $A (2 ， 0)$ ，求抛物线的对称轴；

(2)、已知抛物线上有四个点 $B (- 1 ， y_{1}) ， C (1 ， y_{2}) ， D (3 ， y_{3}) ， E (m ， 0)$ ，且 $2 < m < 4$ ．比较 $y_{1} ， y_{2} ， y_{3}$ 的大小，并说明理由．

查看试题解析

21. 二次函数

y = a x^{2} + b x + c (a ， b ， c

是常数，且

a \neq 0)

的自变量

x

与函数值

y

的部分对应值如表：

$x$	$\dots$	-1	0	3	4	$\dots$
$y$	$\dots$	0	4	$m$	0	$\dots$

(1)、直接写出

m

的值，并求该二次函数的解析式；

(2)、当

1 < x < 5

时，求函数值

y

的取值范围．

查看试题解析

22. 在平面直角坐标系 $x O y$ 中，点 $M (x_{1} ， y_{1})$ ， $N (x_{2} ， y_{2})$ 在抛物线 $y = a x^{2} + b x + 1 (a < 0)$ 上，其中 $x_{1} < x_{2}$ ，设抛物线的对称轴为 $x = t$ ．

(1)、当 $t = 1$ 时，如果 $y_{1} = y_{2} = 1$ ，直接写出 $x_{1}$ ， $x_{2}$ 的值；

(2)、当 $x_{1} = - 1$ ， $x_{2} = 3$ 时，总有 $y_{2} < y_{1} < 1$ ，求t的取值范围．

查看试题解析
23. 设二次函数 $y = (x + 1) (a x + 2 a + 2)$ （ $a$ 是常数， $a \neq 0$ ）

(1)、若 $a = 1$ ，求该函数图象的顶点坐标.

(2)、若该二次函数图象经过 $(- 1 ， 1)$ ， $(- 2 ， 3)$ ， $(0 ， - 2)$ 三个点中的一个点，求该二次函数的表达式.

(3)、若二次函数图象经过 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ 两点，当 $x_{1} + x_{2} = 2$ ， $x_{1} < x_{2}$ 时， $y_{1} > y_{2}$ ，求证： $a < - \frac{2}{5}$

查看试题解析
24. 设二次函数 $y = - x^{2} + b x + c$ （ $b$ ， $c$ 是常数）的图像与 $x$ 轴交于 $A$ ， $B$ 两点.

(1)、若 $A$ ， $B$ 两点的坐标分别为 $(- 1 ， 0)$ ， $(3 ， 0)$ ，求该二次函数的表达式.

(2)、若函数 $y$ 的表达式可以写成 $y = - {(x + h)}^{2} + 3$ （ $h$ 是常数）的形式，求 $c - b$ 的最大值.

(3)、设一次函数 $p = x - m$ （ $m$ 是常数），若二次函数的表达式还可以写成 $y = - (x - m) (x - m + 1)$ 的形式，当函数 $q = y - p$ 的图像经过点 $(x_{0} ， 0)$ 时，求 $x_{0} - m$ 的值.

查看试题解析

$x$	…	-1	0	1	2	3	…
$y$	…	-3	1	3	3	1	…

2023年浙教版数学九年级上册1.3二次函数的性质 同步测试

一、单选题（每题3分，共30分）

二、填空题（每空4分，共24分）

三、解答题（共6题，共66分）

2023年浙教版数学九年级上册1.3二次函数的性质同步测试