人教版八年级上册数学进阶课堂小测——12.1全等三角形(三阶)
试卷更新日期:2023-06-18 类型:同步测试
一、单选题
-
1. 如图,锐角△ABC 中,D 、E 分别是 AB 、AC 边上的点,△ADC≌△ADC',△AEB≌△AEB' , 且C'D∥EB'∥BC , BE 、CD 交于点 F ,若∠BAC = α, ∠BFC = β,则( )
 A、2α+β= 180° B、2β-α= 145° C、α+β= 135° D、β-α= 60°2. 如图,已知在正方形中,厘米, , 点E在边上,且厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段上由C点向D点运动,设运动时间为t秒,当ΔBPE与ΔCQP全等时,t的值为( )
A、2α+β= 180° B、2β-α= 145° C、α+β= 135° D、β-α= 60°2. 如图,已知在正方形中,厘米, , 点E在边上,且厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段上由C点向D点运动,设运动时间为t秒,当ΔBPE与ΔCQP全等时,t的值为( )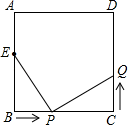 A、2 B、2或1.5 C、2.5 D、2.5或23. 如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD , 正方形EFGH , 正方形MNPQ的面积分别为S1 , S2 , S3 , 若S1+S2+S3=60,则S2的值是( )
A、2 B、2或1.5 C、2.5 D、2.5或23. 如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD , 正方形EFGH , 正方形MNPQ的面积分别为S1 , S2 , S3 , 若S1+S2+S3=60,则S2的值是( ) A、12 B、15 C、20 D、254. 如图,N,C,A三点在同一直线上,△ABC中,∠A:∠ABC:∠ACB=3:5:10.若△MNC≌△ABC,则∠BCM的度数为( )
A、12 B、15 C、20 D、254. 如图,N,C,A三点在同一直线上,△ABC中,∠A:∠ABC:∠ACB=3:5:10.若△MNC≌△ABC,则∠BCM的度数为( ) A、20° B、25° C、28° D、30°5. 如果的三边长分别为3,5,7,的三边长分别为3, , , 若这两个三角形全等,则( )A、8 B、或6 C、10 D、或66. 如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且 ,BE、CD交于点F.若∠BAC=40°,则∠BFC的大小是( )
A、20° B、25° C、28° D、30°5. 如果的三边长分别为3,5,7,的三边长分别为3, , , 若这两个三角形全等,则( )A、8 B、或6 C、10 D、或66. 如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且 ,BE、CD交于点F.若∠BAC=40°,则∠BFC的大小是( ) A、105° B、110° C、100° D、120°
A、105° B、110° C、100° D、120°二、填空题
-
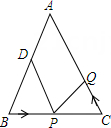
7. 如图,在△ABC中,AB=AC=24厘米,∠B=∠C ,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
 8. 如图,在中, , , , 一条线段 , , 两点分别在线段和的垂线上移动,若以为顶点的三角形与以为顶点的三角形全等,则的值为.
8. 如图,在中, , , , 一条线段 , , 两点分别在线段和的垂线上移动,若以为顶点的三角形与以为顶点的三角形全等,则的值为. 9. 在平面直角坐标系中,已知 , , , 若 , 则点D的坐标为.10. 如图,直线PQ经过Rt△ABC的直角顶点C,△ABC的边上有两个动点D、E,点D以1cm/s的速度从点A出发,沿AC→CB移动到点B,点E以3cm/s的速度从点B出发,沿BC→CA移动到点A,两动点中有一个点到达终点后另一个点继续移动到终点.过点D、E分别作DM⊥PQ,EN⊥PQ,垂足分别为点M、N,若AC=6cm,BC=8cm,设运动时间为t,则当t= s时,以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等.
9. 在平面直角坐标系中,已知 , , , 若 , 则点D的坐标为.10. 如图,直线PQ经过Rt△ABC的直角顶点C,△ABC的边上有两个动点D、E,点D以1cm/s的速度从点A出发,沿AC→CB移动到点B,点E以3cm/s的速度从点B出发,沿BC→CA移动到点A,两动点中有一个点到达终点后另一个点继续移动到终点.过点D、E分别作DM⊥PQ,EN⊥PQ,垂足分别为点M、N,若AC=6cm,BC=8cm,设运动时间为t,则当t= s时,以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等.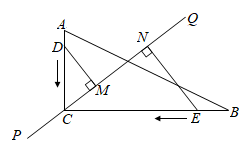 11. 如图, , 于A, 于B,且 ,P在线段 上,Q在射线 上,若 与 全等,则 .
11. 如图, , 于A, 于B,且 ,P在线段 上,Q在射线 上,若 与 全等,则 . 12. 如图,已知AC平分∠DAB , CE⊥AB于点E , AB=AD+2BE , 则下列结论:①AB+AD= 2AE;②∠DAB+∠DCB=180°;③CD=CB;④SACE﹣SBCE=SACD . 其中正确的是 .
12. 如图,已知AC平分∠DAB , CE⊥AB于点E , AB=AD+2BE , 则下列结论:①AB+AD= 2AE;②∠DAB+∠DCB=180°;③CD=CB;④SACE﹣SBCE=SACD . 其中正确的是 .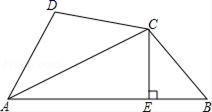 13. 如图,坐标平面上,△ABC≌△DEF,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B,C两点的纵坐标都是-3,D,E两点在y轴上,则点F到y轴的距离为.
13. 如图,坐标平面上,△ABC≌△DEF,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B,C两点的纵坐标都是-3,D,E两点在y轴上,则点F到y轴的距离为.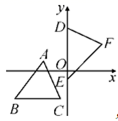 14. 如图,直线 经过 的直角顶点 的边上有两个动点 ,点 以 的速度从点 出发沿 移动到点 ,点 以 的速度从点 出发,沿 移动到点 ,两动点中有一个点到达终点后另一个点继续移动到终点过点 分别作 ,垂足分别为点 .若 ,设运动时间为 ,则当 时,以点 为顶点的三角形与以点 为顶点的三角形全等.
14. 如图,直线 经过 的直角顶点 的边上有两个动点 ,点 以 的速度从点 出发沿 移动到点 ,点 以 的速度从点 出发,沿 移动到点 ,两动点中有一个点到达终点后另一个点继续移动到终点过点 分别作 ,垂足分别为点 .若 ,设运动时间为 ,则当 时,以点 为顶点的三角形与以点 为顶点的三角形全等.
三、解答题

