安徽省合肥市包河区2022-2023学年八年级下册期末数学考试仿真卷【二】
试卷更新日期:2023-06-17 类型:期末考试
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 利用配方法解一元二次方程时,将方程配方为 , 则、的值分别为( )A、 , B、 , C、 , D、 ,4. 以为根的一元二次方程可能是( )A、 B、 C、 D、5. 如图所示,某景区内有一块长方形油菜花田地(单位:m),现在其中修建一条观花道(阴影部分)供游人赏花,要求观花道的面积占长方形油菜花田地面积的 . 设观花道的直角边(如图所示)为x,则可列方程为( )
 A、 B、 C、 D、6. 智能垃圾箱分为“有害垃圾、可回收垃圾”等若干箱体.居民通过刷卡、手机号、人脸识别等身份识别方式进行自动开箱投放,将不同的垃圾投放至不同的箱体内,垃圾箱则根据居民投放的垃圾,自动进行称重,然后换算出积分可以现金提现或在礼品兑换机兑换实物礼品.我市某小区7个家庭一周换算的积分分别为23,25,25,23,30,27,25.关于这组数据,中位数和众数分别是( )A、23,25 B、25,23 C、23,23 D、25,257. 下面命题不正确的是( )A、有两个锐角互余的三角形是直角三角形. B、如果三角形的较短两边的平方和等于最长边的平方,那么这个三角形是直角三角形. C、如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形. D、如果三角形的三个内角之比是3:4:5,那么这个三角形是直角三角形8. 勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的, , , ,点 都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
A、 B、 C、 D、6. 智能垃圾箱分为“有害垃圾、可回收垃圾”等若干箱体.居民通过刷卡、手机号、人脸识别等身份识别方式进行自动开箱投放,将不同的垃圾投放至不同的箱体内,垃圾箱则根据居民投放的垃圾,自动进行称重,然后换算出积分可以现金提现或在礼品兑换机兑换实物礼品.我市某小区7个家庭一周换算的积分分别为23,25,25,23,30,27,25.关于这组数据,中位数和众数分别是( )A、23,25 B、25,23 C、23,23 D、25,257. 下面命题不正确的是( )A、有两个锐角互余的三角形是直角三角形. B、如果三角形的较短两边的平方和等于最长边的平方,那么这个三角形是直角三角形. C、如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形. D、如果三角形的三个内角之比是3:4:5,那么这个三角形是直角三角形8. 勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的, , , ,点 都在矩形KLMJ的边上,则矩形KLMJ的面积为( ) A、360 B、400 C、440 D、4849. 如图,在△ABC中,∠B=90°,AB=BC=4,把△ABC绕点A逆时针旋转45°得到△ADE,过点C作CF⊥AE于F,DE交CF于G,则四边形ADGF的周长是( )
A、360 B、400 C、440 D、4849. 如图,在△ABC中,∠B=90°,AB=BC=4,把△ABC绕点A逆时针旋转45°得到△ADE,过点C作CF⊥AE于F,DE交CF于G,则四边形ADGF的周长是( ) A、8 B、4+4 C、8+ D、810. 如图,在等腰 中, , , 是 边上的中点,点 、 分别在 、 边上运动,且保持 ,连接 、 、 .在此运动变化过程中,下列结论:① 是等腰直角三角形;②四边形 不可能为正方形;③ 长度的最小值为2;④四边形 的面积保持不变;⑤ 面积的最大值为2.其中正确的结论是( )
A、8 B、4+4 C、8+ D、810. 如图,在等腰 中, , , 是 边上的中点,点 、 分别在 、 边上运动,且保持 ,连接 、 、 .在此运动变化过程中,下列结论:① 是等腰直角三角形;②四边形 不可能为正方形;③ 长度的最小值为2;④四边形 的面积保持不变;⑤ 面积的最大值为2.其中正确的结论是( ) A、①②③ B、①④⑤ C、①③④ D、③④⑤
A、①②③ B、①④⑤ C、①③④ D、③④⑤二、填空题
-
11. 若最简二次根式 与 是同类二次根式,则a= .12. 数学家发明了一个魔术盒,当任意实数对进入其中时,会得到一个新的实数: . 例如把放入其中,就会得到 . 现将实数对放入其中得到实数m,再将实数对放入其中后,得到的实数是 .13. 若一组数据1,3,a,2,5的平均数是3,则这组数据的方差是14. 已知关于x的一元二次方程有两个相等的实数根,则的值等于 .15. 如图,在矩形ABCD中, , , 点P在BC边上,点M在AD边上, , 点Q为AP的中点,当为直角三角形时,AP的长为 .

三、计算题
-
16.(1)、计算:( ﹣1)0+3×(﹣2)+(2)、化简:(x+2)2﹣x(x+2)
四、作图题
-
17.(1)、问题背景:在△ABC中,AB,BC,AC三边的长分别为 ,求这个三角形的面积,小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点(即三个顶点都在小正方形的顶点处),如图所示,这样不需要求高,而借用网格就能计算出它的面积.请将△ABC的面积直接填写在横线上.
 (2)、思维拓展:我们把上述求△ABC面积的方法叫做构图法,若△ABC中,AB,BC,AC三边长分别为 ,2 (a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,直接写出此三角形最长边上的高是.
(2)、思维拓展:我们把上述求△ABC面积的方法叫做构图法,若△ABC中,AB,BC,AC三边长分别为 ,2 (a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,直接写出此三角形最长边上的高是.五、综合题
-
18. 已知关于的一元二次方程 , 其中 , , 分别为三边的长.(1)、如果是方程的根,试判断的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断的形状,并说明理由;(3)、如果是等边三角形,试求这个一元二次方程的根.19. 如图,在中,过点D作于点E,点F在边上, , 连接 .
 (1)、求证:四边形是矩形;(2)、若 , 求证:平分 .20. 乐清附虹银泰商场于今年年初以每件25元的进价购进一批商品,当商品售价为40元时,一月份销售256件,二、三月该商品十分畅销,销售量持续走高,在售价不变的基础上,三月份的销售量达到400件,设二、三这两个月月平均增长率不变.(1)、求二、三这两个月月平均增长率.(2)、从四月份起,商场采用降价促销的方式回馈顾客,经调查发现该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?21. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
(1)、求证:四边形是矩形;(2)、若 , 求证:平分 .20. 乐清附虹银泰商场于今年年初以每件25元的进价购进一批商品,当商品售价为40元时,一月份销售256件,二、三月该商品十分畅销,销售量持续走高,在售价不变的基础上,三月份的销售量达到400件,设二、三这两个月月平均增长率不变.(1)、求二、三这两个月月平均增长率.(2)、从四月份起,商场采用降价促销的方式回馈顾客,经调查发现该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?21. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图: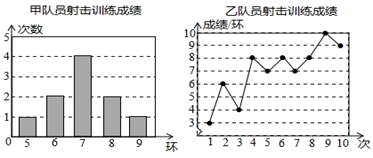
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
乙
(1)、写出表格中 的值:(2)、分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?说明你的理由。
22. 如图1,正方形中,点E是延长线上一点,连接 , 过点B作于点F,交于点G.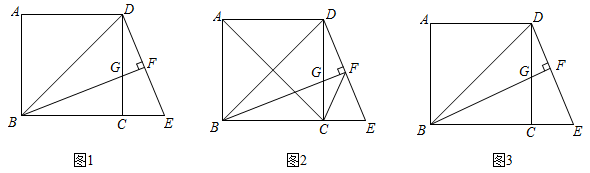 (1)、求证: .(2)、如图2,连接、 . 若平分 , 求证:平分 .(3)、如图3,若G为中点, , 求的长.
(1)、求证: .(2)、如图2,连接、 . 若平分 , 求证:平分 .(3)、如图3,若G为中点, , 求的长.六、附加题
-
23. 若
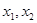 是方程 的两个实数根,且
是方程 的两个实数根,且 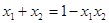 ,则 的值为.
,则 的值为.
-
-