上海市青浦区2023年中考二模数学试卷

试卷更新日期：2023-06-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列二次根式中，最简二次根式的是（）

A、 $\sqrt{0.2}$ B、 $\sqrt{8}$ C、 $\sqrt{6}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
2. 下列计算中，正确的是（）

A、 ${(a^{3})}^{4} = a^{7}$ B、 $a^{2} \cdot a^{6} = a^{8}$ C、 $a^{3} + a^{3} = a^{6}$ D、 $a^{8} \div a^{4} = a^{2}$

查看试题解析
3. 下列关于x的方程一定有实数解的是（）

A、 $4 x^{2} + 9 = 0$ B、 $x^{2} + x - 2 = 0$ C、 $\sqrt{x - 2} = 1 - x$ D、 $\frac{x + 1}{x - 1} = \frac{2}{x - 1}$

查看试题解析
4. 在学校举办的“诗词大赛”中，有9名选手进入决赛，他们的决赛成绩各不相同，其中一名选手想知道自己是否能进入前5名，除了知道自己的成绩外，他还需要了解这9名学生成绩的（）

A、中位数 B、平均数 C、众数 D、方差．

查看试题解析
5. 已知平行四边形 $A B C D$ 的对角线 $A C 、 B D$ 相交于点O．下列补充条件中，能判定这个平行四边形是菱形的是（）

A、 $O A = O C$ B、 $O A = O B$ C、 $∠ A B D = ∠ C B D$ D、 $∠ A B D = ∠ C A B$

查看试题解析
6. 关于某个函数表达式，甲、乙、丙三位同学都正确地说出了该函数的一个特征．甲：函数图象经过点 $(- 2 ， 2)$ ；乙：函数图象经过第四象限；丙：当 $x > 0$ 时，y随x的增大而增大．则这个函数表达式可能是（）

A、 $y = - x$ B、 $y = x + 4$ C、 $y = \frac{1}{2} x^{2}$ D、 $y = - \frac{4}{x}$

查看试题解析

二、填空题

7. 函数 $y = \frac{1}{x + 1}$ 的定义域是．

查看试题解析
8. 因式分解： $a^{2} - a b =$ ．

查看试题解析
9. 方程 $\sqrt{2 x - 3}$ =1的解是．

查看试题解析
10. 不等式组 ${\begin{array}{l} - 2 x < 3 \\ x - 1 < 0 \end{array}$ 的解集是．

查看试题解析
11. 在 $- 1$ 、 $1$ 、 $2$ 这三个数中任取两个数作为点P（x，y）的横坐标和纵坐标，那么在平面直角坐标系xOy内，点P在第二象限的概率为．

查看试题解析
12. 若一个正多边形的每一个外角都等于36°，那么这个正多边形的中心角为度.

查看试题解析
13. 已知点 $M (- 1 ， 2)$ 和点 $N$ 都在抛物线 $y = x^{2} - 2 x + c$ 上，如果 $M N ∥ x$ 轴，那么点N的坐标为．

查看试题解析
14. 已知点 $G$ 为 $△ A B C$ 的重心， $\vec{A B} = \vec{a}$ ， $\vec{A C} = \vec{b}$ ，那么 $\vec{A G} =$ __．（用 $\vec{a}$ 、 $\vec{b}$ 表示）

查看试题解析
15. 如图，图中反映轿车剩余油量q(升)与行驶路径s(千米)的函数关系，那么q与s的函数解析式为．

查看试题解析
16. 水平放置的圆柱形油槽的圆形截面如图2所示，如果该截面油的最大深度为 $2$ 分米，油面宽度为 $8$ 分米，那么该圆柱形油槽的内半径为分米．

查看试题解析
17. 如图3，在平面直角坐标系 $x O y$ 内，已知点 $G (- 3 ， 1)$ ， $A (- 1 ， 3)$ ， $B (- 4 ， 0)$ ，如果 $⊙ C$ 是以线段 $A B$ 为直径的圆，那么点G与 $⊙ C$ 的最短距离为．

查看试题解析

三、解答题

18. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 ° ， B C = 6 ， A B = 10$ ，点D是边 $A B$ 的中点，点M在边 $A C$ 上，将 $△ A D M$ 沿 $D M$ 所在的直线翻折，点A落在点E处，如果 $E C ∥ A B$ ，那么 $C E =$ ．

查看试题解析
19. 计算： $| \sqrt{2} - 1 | + {(\frac{1}{2})}^{- 2} + \frac{1}{\sqrt{2} + 1} - 8^{\frac{1}{2}}$

查看试题解析
20. 解方程组： ${\begin{matrix} x^{2} - 9 y^{2} = 0 \begin{matrix} \end{matrix} ① \\ x^{2} - 2 x y + y^{2} = 4 ② \end{matrix}$

查看试题解析
21. 如图5，在 $△ A B C$ 中，已知 $B C = 12$ ， $\tan B = \frac{1}{2}$ ， $∠ C = 45 °$ ．

(1)、求边 $A B$ 的长；

(2)、已知点D在 $A B$ 边上，且 $\frac{A D}{B D} = \frac{1}{3}$ ，连接 $C D$ ，试说明 $∠ B C D$ 与 $∠ B$ 相等．

查看试题解析
22. 某中学初三年级在“阳光体育”活动中，参加各项球类运动的数据信息制作成了扇形统计图，如图所示.已知参加乒乓球运动的人数有80人，请根据图中的信息解决下列问题.

(1)、求参加篮球和足球运动的总人数；

(2)、学校为本次活动购买了一些体育器材，其中购买的篮球和足球的数量是根据参加的人数每人一只配备的，购买篮球的费用是3000元，购买足球费用是2400元，并且篮球的单价比足球的单价便宜10元.请你帮助计算一下，参加篮球运动和足球运动的学生各有多少人？

查看试题解析
23. 如图，在平行四边形ABCD中，已知 $B D$ 平分 $∠ A B C$ ，点E在边 $B C$ 上，联结 $A E$ 交 $B D$ 于点F，且 $A B^{2} = B F \cdot B D$ ．

(1)、求证：点F在边 $A B$ 的垂直平分线上；

(2)、求证： $A D \cdot A E = B E \cdot B D$ ．

查看试题解析
24. 如图，已知抛物线 $y = - \frac{1}{4} x^{2} + b x + c$ 经过点 $B (6 ， 0)$ 和 $C (0 ， 3)$ ，与x轴的另一个交点为点A．

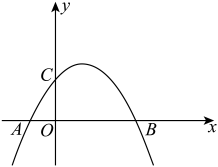(1)、求抛物线的解析式及点A的坐标；

(2)、将该抛物线向右平移m个单位 $(m > 0)$ ，点C移到点D，点A移到点E，若 $∠ D E C = 90 °$ ，求m的值；

(3)、在（2）的条件下，设新抛物线的顶点为G，新抛物线在对称轴右侧的部分与x轴交于点F，求点C到直线 $G F$ 的距离．

查看试题解析
25. 如图，半圆O的直径 $A B = 10$ ，点C在半圆O上， $B C = 6 ， C H ⊥ A B$ ，垂足为点H，点D是弧AC上一点．

(1)、若点D是弧 $A B$ 的中点，求 $t a n ∠ D O C$ 的值；

(2)、连接 $B D$ 交半径 $O C$ 于点E，交 $C H$ 于点F，设 $O E = m$ ．
①用含m的代数式表示线段 $C F$ 的长；

②分别以点O为圆心 $O E$ 为半径、点C为圆心 $C F$ 为半径作圆，当这两个圆相交时，求m取值范围．

查看试题解析