上海市普陀区2023年中考二模数学卷
试卷更新日期:2023-06-17 类型:中考模拟
一、单选题
-
1. 中国是最早认识正数和负数的国家,魏晋时期的数学家刘徽就提出了负数的概念,如果将零下记作 , 那么表示( )A、零上 B、零下 C、零上 D、零下2. 下列算式中,计算结果为的是( )A、 B、 C、 D、3. 已知函数(k是常数,)的图像经过第一、三象限,下列说法中正确的是( )A、 B、图像一定经过点 C、图像是双曲线 D、的值随的值增大而减小4. 某城市30天的空气质量状况统计如下:
空气质量指数()
40
60
90
110
120
140
天数
2
5
10
1
根据表中的信息,下列有关该城市这30天的空气质量指数的统计量中,可以确定的量是( )
A、平均数 B、众数 C、中位数 D、方差5. 如果用两根长度相同的细竹签作对角线,制作一个四边形的风筝,那么做成的风筝形状不可能是( )A、矩形 B、正方形 C、等腰梯形 D、直角梯形6. 如图,中, , 、分别平分、 , , 下面结论中不一定正确的是( ) A、 B、 C、 D、点O到直线的距离是1
A、 B、 C、 D、点O到直线的距离是1二、填空题
-
7. 因式分解: .
8. 已知 , 那么 .9. 方程的根是 .10. 如果关于x的方程有两个相等的实数根,那么 .11. 近视眼镜的度数(度)与镜片焦距(米)成反比例,已知400度的近视眼镜镜片的焦距为0.25米,那么眼镜度数关于镜片焦距的函数解析式是 .12. 一个三角形的两边长分别是2和3,若它的第三边长为奇数,则这个三角形的周长为 .13. 不透明的布袋中装有除颜色外完全相同的10个球,其中红色球有个,如果从布袋中任意摸出一个球恰好为红色球的概率是 , 那么 .14. 学校为了解本校初三年级学生上学的交通方式,随机抽取了本校20名初三学生进行调查,其中有2名学生是乘私家车上学,如图是收集数据后绘制的扇形图.如果该校初三年级有200名学生,那么骑自行车上学的学生大约有人.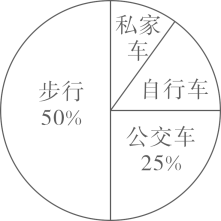 15. 如图,斜坡的坡度 , 现需要在不改变坡高的情况下将坡度变缓,调整后的斜坡的坡度 , 已知斜坡米,那么斜坡米.
15. 如图,斜坡的坡度 , 现需要在不改变坡高的情况下将坡度变缓,调整后的斜坡的坡度 , 已知斜坡米,那么斜坡米. 16. 如图, , 、交于点 , , 设 , , 那么向量用向量、表示为 .
16. 如图, , 、交于点 , , 设 , , 那么向量用向量、表示为 . 17. 在矩形中, , , 点在边上, , 以点为圆心、为半径作(如图),点在边上,以点为圆心、为半径作 . 如果与外切,那么的长是 .
17. 在矩形中, , , 点在边上, , 以点为圆心、为半径作(如图),点在边上,以点为圆心、为半径作 . 如果与外切,那么的长是 . 18. 在中, , , , 为中点(如图),为射线上一点,将沿着翻折得到 , 点的对应点为 , 如果 , 那么 .
18. 在中, , , , 为中点(如图),为射线上一点,将沿着翻折得到 , 点的对应点为 , 如果 , 那么 .
三、解答题
-
19. 计算: .20. 解不等式组:并把解集在数轴上表示出来.
 21. 如图,在中, , 垂足为点 , , , , .
21. 如图,在中, , 垂足为点 , , , , . (1)、求的长;(2)、求的面积.22. 购物节期间,、两家网店分别推出了促销活动,店活动:当购买的商品总金额在200元及以内,不享受折扣,当购买的商品总金额超过200元,超过200元的金额打折,店购物的实付总金额(元)与商品总金额(元)之间的函数关系如图所示;店活动:所有商品直接打七折.
(1)、求的长;(2)、求的面积.22. 购物节期间,、两家网店分别推出了促销活动,店活动:当购买的商品总金额在200元及以内,不享受折扣,当购买的商品总金额超过200元,超过200元的金额打折,店购物的实付总金额(元)与商品总金额(元)之间的函数关系如图所示;店活动:所有商品直接打七折. (1)、当A店购买的商品总金额超过200元时,求出与之间的函数解析式;(2)、A店推出的促销活动中:;(3)、某公司计划购买某种型号的优盘,采购员发现店的单价要比店的单价贵元,如果购买相同数量的优盘,在店的实付总金额是800元,而在店的实付总金额是819元.请求出店这种型号优盘的单价.23. 已知:如图,四边形中, , , 对角线、相交于点 , 点在边上, , 垂足为点 , .
(1)、当A店购买的商品总金额超过200元时,求出与之间的函数解析式;(2)、A店推出的促销活动中:;(3)、某公司计划购买某种型号的优盘,采购员发现店的单价要比店的单价贵元,如果购买相同数量的优盘,在店的实付总金额是800元,而在店的实付总金额是819元.请求出店这种型号优盘的单价.23. 已知:如图,四边形中, , , 对角线、相交于点 , 点在边上, , 垂足为点 , . (1)、求证:四边形为矩形;(2)、过点作交于点 , 求证: .24. 在平面直角坐标系中(如图),已知抛物线()与x轴交于点和 , 与y轴交于点 . 抛物线的顶点为点 .
(1)、求证:四边形为矩形;(2)、过点作交于点 , 求证: .24. 在平面直角坐标系中(如图),已知抛物线()与x轴交于点和 , 与y轴交于点 . 抛物线的顶点为点 . (1)、求抛物线的表达式,并写出点的坐标;(2)、将直线绕点顺时针旋转,交轴于点 . 此时旋转角等于 .
(1)、求抛物线的表达式,并写出点的坐标;(2)、将直线绕点顺时针旋转,交轴于点 . 此时旋转角等于 .①求点的坐标;
②二次函数的图象始终有一部分落在的内部,求实数的取值范围.
25. 如图,半圆的直径 , 点是上一点(不与点、重合),点是的中点,分别连接、 .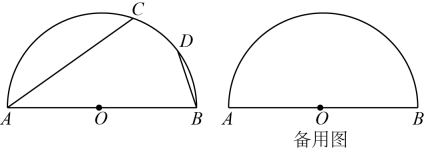 (1)、当是圆的内接正六边形的一边时,求的长;(2)、设 , , 求与之间的函数解析式,并写出x的取值范围;(3)、定义:三角形一边上的中线把这个三角形分成两个小三角形,如果其中有一个小三角形是等腰三角形,且这条中线是这个小三角形的腰,那么这条中线就称为这个三角形的中腰线.分别延长、相交于点 , 连接 . 是的中腰线,求的长.
(1)、当是圆的内接正六边形的一边时,求的长;(2)、设 , , 求与之间的函数解析式,并写出x的取值范围;(3)、定义:三角形一边上的中线把这个三角形分成两个小三角形,如果其中有一个小三角形是等腰三角形,且这条中线是这个小三角形的腰,那么这条中线就称为这个三角形的中腰线.分别延长、相交于点 , 连接 . 是的中腰线,求的长.