安徽省合肥市包河区2022-2023学年八年级下册期末数学考试仿真卷【一】

试卷更新日期：2023-06-17 类型：期末考试

进入出卷网下载

一、单选题

1. 关于x的代数式 $\frac{1}{\sqrt{1 - x}}$ 在实数范围内有意义，则x的取值范围为（）

A、 $x \leq 1$ B、 $x \geq 1$ C、 $x < 1$ D、 $x > 1$

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{4} + \sqrt{9} = \sqrt{13}$ B、 $5 y^{3} \cdot 3 y^{5} = 15 y^{15}$ C、 $\frac{3}{\sqrt{6}} = \frac{\sqrt{6}}{2}$ D、 $3 x^{2} y + 2 x y^{2} = 5 x^{2} y^{2}$

查看试题解析
3. 下列条件中，能够判断△ABC为直角三角形的是（）

A、 $A B = 6$ ， $B C = 8$ ， $A C = 10$ B、 $A B ： B C ： A C = 1 ： 2 ： 3$ C、 $∠ A = ∠ B = ∠ C$ D、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$

查看试题解析
4. 用配方法解一元二次方程 $x^{2} - 4 x + 2 = 0$ 化成 ${(x + a)}^{2} = b$ 的形式，则 $a$ 、 $b$ 的值分别是（）

A、-4，14 B、4，14 C、2，2 D、-2，2

查看试题解析
5. 如图，边长相等的正五边形和正六边形如图拼接在一起，则 $∠ A B C$ 的度数为（）

A、 $22 °$ B、 $23 °$ C、 $24 °$ D、 $25 °$

查看试题解析
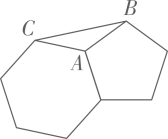6. 如果m，n是两个不相等的实数，且满足 $m^{2} + m = 3$ ， $n^{2} + n = 3$ ，那么代数式 $3 n^{2} - m n - 3 m$ 的值是（）

A、16 B、15 C、12 D、9

查看试题解析
7. 若样本 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $\dots x_{n}$ 的平均数为 $18$ ，方差为 $2$ ，则对于样本 $x_{1} + 3$ ， $x_{2} + 3$ ， $x_{3} + 3$ ， $\dots x_{n} + 3$ ，下列结论正确的是（）

A、平均数为 $21$ ，方差为 $2$ B、平均数为 $21$ ，方差为 $4$ C、平均数为 $18$ ，方差为 $2$ D、平均数为 $18$ ，方差为 $4$

查看试题解析
8. 随着网络直播平台的快速发展，直播砍价已让很多人趋之若鹜，某商品原售价为120元，在某直播平台上经过主播的两次砍价后，现售价为43.2元，已知每次砍价的百分率相同．设每次砍价的百分率为x，则下列方程正确的是（）

A、 $120 (1 - 2 x) = 43.2$ B、 $120 (1 - x)^{2} = 43.2$ C、 $120 (1 - x) + 120 (1 - x)^{2} = 43.2$ D、 $120 (1 - x) + 120 (1 - 2 x) = 43.2$

查看试题解析
9. 如图所示，顺次连接四边形 $A B C D$ 各边中点得到四边形 $E F G H$ ，使四边形 $E F G H$ 为正方形，应添加的条件分别是（）

A、 $A B ∥ C D$ 且 $A B = D C$ B、 $A B = C D$ 且 $A C ⊥ B D$ C、 $A B ∥ C D$ 且 $A C ⊥ B D$ D、 $A C = B D$ 且 $A C ⊥ B D$

查看试题解析
10. 如图所示，在菱形ABCD中，AB＝6，∠BAD＝120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．当点E、F在BC、CD上滑动时，△CEF的面积最大值是（）

A、4 $\sqrt{3}$ B、 $\frac{5}{4} \sqrt{3}$ C、3 $\sqrt{3}$ D、 $\frac{9}{4} \sqrt{3}$

查看试题解析

二、填空题

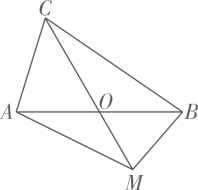
11. 当x=时，最简二次根式 $\sqrt{3 x + 5}$ 与 $2 \sqrt{2 x + 7}$ 能够合并．

查看试题解析
12. 设 $α$ ， $β$ 是一元二次方程 $x^{2} + 3 x - 7 = 0$ 的两个根，则 $a^{2} + 4 α + β =$ ．

查看试题解析
13. 如图，在△ABC中，AB＝BC＝8，AO＝BO，点M是射线CO上的一个动点，∠AOC＝60°，则当△ABM为直角三角形时，AM的长为.

查看试题解析
14. 勾股定理最早出现在商高的《周髀算经》：“勾广三，股修四，经隅五”.观察下列勾股数：3，4，5；5，12，13；7，24，25；…，这类勾股数的特点是：勾为奇数，弦与股相差为1，柏拉图研究了勾为偶数，弦与股相差为2的一类勾股数，如：6，8，10；8，15，17；…，若此类勾股数的勾为2m（m≥3，m为正整数），则其弦是（结果用含m的式子表示）.

查看试题解析
15. 如图，在矩形 $A B C D$ 中， $A B = 10$ ， $A D = 12$ ，点N是 $A B$ 边上的中点，点M是 $B C$ 边上的一动点连接 $M N$ ，将 $△ B M N$ 沿 $M N$ 折叠，若点B的对应点 $B^{'}$ ，连接 $B^{'} C$ ，当 $△ B^{'} M C$ 为直角三角形时， $B M$ 的长为．

查看试题解析

三、计算题

16.

(1)、计算： $\sqrt{\frac{1}{2}} \times \sqrt{8} - (- 2 \sqrt{3})^{0} + (- \frac{1}{3})^{- 1}$ ；

(2)、解方程： $x^{2} - 2 x = 9$ ．

查看试题解析

四、作图题

17. 如图，四边形 $A B C D$ 是平行四边形，点 $E$ 在 $C D$ 延长线上，连接 $B E$ ， $A E$ ．

(1)、在图甲中画出一个以 $A B$ 为边的平行四边形，且它的周长等于 $6 \sqrt{5}$ ；

(2)、在图乙中画出一个以 $A B$ 为对角线的平行四边形，且它的面积为12．

查看试题解析

五、综合题

18. 已知关于 $x$ 的方程 $k x^{2} - 2 (k + 1) x + k - 1 = 0$ 有两个不相等的实数根．

(1)、求 $k$ 的取值范围．

(2)、是否存在实数 $k$ ，使此方程的两个实数根的倒数和等于1？若存在，求出 $k$ 的值：若不存在，说明理由．

查看试题解析
19. 如图，在平行四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ，点 $E$ ， $F$ 在 $A C$ 上，点 $G$ ， $H$ 在 $B D$ 上．

(1)、若 $A C = A D$ ， $∠ C A D = 50 °$ ，求 $∠ B C D$ 的度数；

(2)、若四边形 $E H F G$ 是平行四边形，求证： $A E = C F$ ．

查看试题解析
20. 在蚌埠花博园附近某盆栽销售处发现：进货价为每盆50元，销售价为每盆80元的某盆栽平均每天可售出20盆．现此店决定采取适当的降价措施，扩大销售量，增加盈利．经市场调查发现：如果每盆降价2元，那么平均每天就可多售出3盆，设每盆降价x元．

(1)、现在每天卖出盆，每盆盈利元（用含 $x$ 的代数式表示）；

(2)、求当 $x$ 为何值时，平均每天销售这种盆栽能盈利700元，同时又要使顾客得到较多的实惠；

(3)、要想平均每天盈利1000元，可能吗？请说明理由．

查看试题解析

21. 争创全国文明城市

— —

从我做起

.

某中学开设了文明礼仪校本课程，为了解学生的学习情况，学校组织七八年级学生进行文明礼仪知识测试，两个年级均有300名学生，从七八年级各随机抽取了10名学生的测试成绩，满分100分，整理分析如下：

七年级：99，98，98，98，95，93，91，90，89，79

八年级：99，99，99，91，96，90，93，87，91，85

整理分析上面的数据，得到如下表格：

年级 $/$ 统计量	平均数	中位数	众数	方差
七年级	93	94	$a$	33.7
八年级	93	$b$	99	23.4

根据以上信息，解答下列问题．

(1)、填空：

a =

，

b =

；

(2)、根据统计结果，年级的成绩更整齐；

(3)、七年级小齐同学和八年级小钟同学成绩均为93分，根据上面统计情况估计同学的成绩在本年级的排名更靠前；

(4)、如果在收集七年级数据的过程中将抽取的“89”误写成了“79”，七年级数据的平均数、中位数、众数中发生变化的是；

(5)、若成绩不低于95分的可以获奖，估计两个年级获奖的共有多少人？

查看试题解析

22. 如图，正方形 $A B C D$ 中，点P是边 $C D$ 上的一点（不与点C、D重合），连接 $B P$ ， $∠ P B C = α$ ， O为 $B P$ 的中点，过点P作 $P E ⊥ B D$ 于E ，连接 $E O ， A E$ ．

(1)、依题意补全图形；

(2)、求 $∠ P O E$ 的大小（用含a的式子表示）；

(3)、用等式表示线段 $A E$ 与 $B P$ 之间的数量关系，并证明．

查看试题解析

六、附加题

23. 关于x的方程 $x^{2} - 2 x + m = p^{2}$ ，无论实数p取何值，该方程总有两个不相等的实数根，则实数m的取值范围为.

查看试题解析