吉林省长春市榆树市市北片五校2023年中考数学二模试卷
试卷更新日期:2023-06-17 类型:中考模拟
一、单选题
-
1. 若运算“1□(﹣2)”的结果为正数,则□内的运算符号为( )A、+ B、﹣ C、× D、÷2. 在长春市“暖房子工程”实施过程中,某工程队做了面积为632000的外墙保暖,632000这个数用科学记数法表示为( )A、 B、 C、 D、3. 下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是( )A、
 B、
B、 C、
C、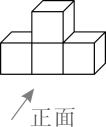 D、
D、 4. 不等式组 的解集为( )A、 B、 C、 D、5. 泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( )
4. 不等式组 的解集为( )A、 B、 C、 D、5. 泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( ) A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似6. 如图,直线a∥b,∠1=75°,∠2=40°,则 ∠3的度数为( )
A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似6. 如图,直线a∥b,∠1=75°,∠2=40°,则 ∠3的度数为( )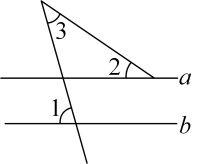 A、75° B、50° C、35° D、30°7. 已知,如图,在菱形ABCD中.(1)分别以C , D为圆心,大于 长为半径作弧,两弧分别交于点E , F;(2)作直线EF , 且直线EF恰好经过点A , 且与边CD交于点M;(3)连接BM . 根据以上作图过程及所作图形,判断下列结论中错误的是( )
A、75° B、50° C、35° D、30°7. 已知,如图,在菱形ABCD中.(1)分别以C , D为圆心,大于 长为半径作弧,两弧分别交于点E , F;(2)作直线EF , 且直线EF恰好经过点A , 且与边CD交于点M;(3)连接BM . 根据以上作图过程及所作图形,判断下列结论中错误的是( ) A、∠ABC=60° B、如果AB=2,那么BM=4 C、BC=2CM D、8. 如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数 的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点, 的面积为1,则k的值为( )
A、∠ABC=60° B、如果AB=2,那么BM=4 C、BC=2CM D、8. 如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数 的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点, 的面积为1,则k的值为( )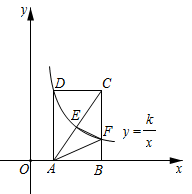 A、 B、 C、2 D、3
A、 B、 C、2 D、3二、填空题
-
9. 比较大小:﹣ ﹣1(填“>”、“=”或“<”)10. 如图是利用网格画出的长春市轨道交通线网图,若建立适当的平面直角坐标系,则表示解放大路的点的坐标为 , 表示伪皇宫的点的坐标为 , 则表示胜利公园的点的坐标是 .
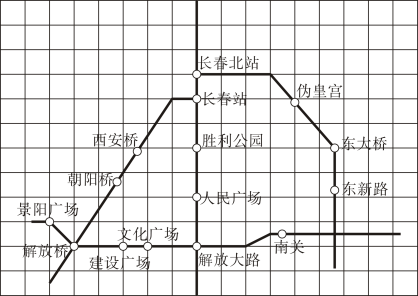 11. 二次函数y=2x2+3x-2的图象与x轴有个交点.12. 圆规两脚形成的角α称为圆规的张角,已知一个圆规两脚的长均为 , 最大的张角为 , 将圆规直立放置;两脚从并拢到形成最大张角,圆规高度下降厘米.(脚的宽度忽略不计)(参考数据: , , )
11. 二次函数y=2x2+3x-2的图象与x轴有个交点.12. 圆规两脚形成的角α称为圆规的张角,已知一个圆规两脚的长均为 , 最大的张角为 , 将圆规直立放置;两脚从并拢到形成最大张角,圆规高度下降厘米.(脚的宽度忽略不计)(参考数据: , , ) 13. 如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形组成,恰好拼成一个大正方形 , 连结并延长交于点M . 若 , , 则的长为 .
13. 如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形组成,恰好拼成一个大正方形 , 连结并延长交于点M . 若 , , 则的长为 . 14. 为了在校运会中取得更好的成绩,小丁积极训练,在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是1.68米,当铅球运行的水平距离为2米时,达到最大高度2米的B处,则小丁此次投掷的成绩是米.
14. 为了在校运会中取得更好的成绩,小丁积极训练,在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是1.68米,当铅球运行的水平距离为2米时,达到最大高度2米的B处,则小丁此次投掷的成绩是米.
三、解答题
-
15. 先化简,再求值 ÷(x﹣ ),其中x= .16. 某校计划在暑假第二周的星期一至星期四开展社会实践活动,要求每位学生选择两天参加活动.(1)、甲同学随机选择两天,请用画树状图(或列表)的方法求其中有一天是星期二的概率?(2)、乙同学随机选择连续的两天,其中有一天是星期二的概率是 .17. 寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用。若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元.(1)、求每副围棋和每副中国象棋各多少元;(2)、寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?18. 在下面的正方形网格中按要求作图.
 (1)、在图①中将平移,使点A与点C重合,得到;(2)、在图②中将绕点C逆时针旋转 , 得到;(3)、在图③中作 , 使其与关于线段对称.19. 已知:如图,在四边形中, , 垂足为M , 过点A作 , 交的延长线于点E .
(1)、在图①中将平移,使点A与点C重合,得到;(2)、在图②中将绕点C逆时针旋转 , 得到;(3)、在图③中作 , 使其与关于线段对称.19. 已知:如图,在四边形中, , 垂足为M , 过点A作 , 交的延长线于点E . (1)、求证:四边形是平行四边形;(2)、若 , 求的长.20. 某校数学兴趣小组设计了一份“你最喜欢的支付方式”调查问卷(每人必选且只能选一种支付方式),在某商场随机调查了部分顾客,并将统计结果绘制成如所示的两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)、求证:四边形是平行四边形;(2)、若 , 求的长.20. 某校数学兴趣小组设计了一份“你最喜欢的支付方式”调查问卷(每人必选且只能选一种支付方式),在某商场随机调查了部分顾客,并将统计结果绘制成如所示的两幅不完整的统计图,请结合图中所给的信息解答下列问题: (1)、随机调查的顾客有人;在扇形统计图中,表示“现金”支付的扇形圆心角的度数 .(2)、将条形统计图补充完整.(3)、若该商场有1800名顾客,请你根据抽样调查结果估计该商场有多少名顾客最喜欢“支付宝”支付.21. 儿童用药的剂量常常按他们的体重来计算,某种药品,体重 的儿童,每次正常服用量为 ;体重 的儿童每次正常服用量为 ;体重在 范围内时,每次正常服用量 是儿童体重 的一次函数中,现实中,该药品每次实际服用量可以比每次正常服用略高一些,但不能超过正常服用量的1.2倍,否则会对儿童的身体造成较大损害.(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若该药品的一种包装规格为 /袋,求体重在什么范围的儿童生病时可以一次服下一袋药?22.(1)、下面是华师版八年级上册数学教材第69页的部分内容.
(1)、随机调查的顾客有人;在扇形统计图中,表示“现金”支付的扇形圆心角的度数 .(2)、将条形统计图补充完整.(3)、若该商场有1800名顾客,请你根据抽样调查结果估计该商场有多少名顾客最喜欢“支付宝”支付.21. 儿童用药的剂量常常按他们的体重来计算,某种药品,体重 的儿童,每次正常服用量为 ;体重 的儿童每次正常服用量为 ;体重在 范围内时,每次正常服用量 是儿童体重 的一次函数中,现实中,该药品每次实际服用量可以比每次正常服用略高一些,但不能超过正常服用量的1.2倍,否则会对儿童的身体造成较大损害.(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若该药品的一种包装规格为 /袋,求体重在什么范围的儿童生病时可以一次服下一袋药?22.(1)、下面是华师版八年级上册数学教材第69页的部分内容.例4:如图,在△ABC中,D是边BC的中点,过点C画直线CE,使CE∥AB,交AD的延长线于点E,求证:AD=ED.

证明:∵CE∥AB(已知)
∴∠ABD=∠ECD,∠BAD=∠CED(两直线平行,内错角相等)
请你将上面的证明过程补充完整.
(2)、如图①,在上面例题的图中,过点D作DF⊥AB于点F . 若AB=9,BC=10,BF=3,则线段AE的长为 .
 (3)、已知一个顶角为120°、腰长为20cm的等腰三角形纸板,把它剪开成两个部分,再重新拼接成一个新的三角形纸板(不重叠),则这个新的三角形纸板周长的最大值为cm.23. 如图,在中, , , . 动点从点出发,沿线段以每秒5个单位长度的速度向终点运动,连结 , 作点关于的对称点 , 连结、 , 设点的运动时间为秒.
(3)、已知一个顶角为120°、腰长为20cm的等腰三角形纸板,把它剪开成两个部分,再重新拼接成一个新的三角形纸板(不重叠),则这个新的三角形纸板周长的最大值为cm.23. 如图,在中, , , . 动点从点出发,沿线段以每秒5个单位长度的速度向终点运动,连结 , 作点关于的对称点 , 连结、 , 设点的运动时间为秒. (1)、线段的长为 .(2)、当点落在内部时,求的取值范围.(3)、当边把的面积分为的两部分时,求线段的长度.(4)、当垂直于的一边时,直接写出的值.24. 在平面直角坐标系中,函数的图象记为G .(1)、当时.
(1)、线段的长为 .(2)、当点落在内部时,求的取值范围.(3)、当边把的面积分为的两部分时,求线段的长度.(4)、当垂直于的一边时,直接写出的值.24. 在平面直角坐标系中,函数的图象记为G .(1)、当时.①求此函数的最大值.
②若点、都在图象G上,且 , 则a的取值范围为 ▲ .
(2)、已知、、、 , 若过图象G的最高点且垂直于y轴的直线将矩形的面积分成的两个部分,求m的值.(3)、若 , 过点C作轴,将图象G在直线上及直线左侧部分的图象记为 , 将沿直线翻折后得到的图象记为 , 和组成图象记为M . 若图象M上有且只有4个点到x轴的距离为1,直接写出m的取值范围.