吉林省长春市榆树市拉林河片2023年中考二模数学试卷
试卷更新日期:2023-06-17 类型:中考模拟
一、单选题
-
1. ﹣6的相反数是( )A、﹣6 B、﹣ C、6 D、2. 北京时间2022年4月16日9时56分,近地点高度约384000米的神舟十三号载人飞船返回舱成功着陆,圆满完成任务,384000这个数用科学记数法表示为( )A、 B、 C、 D、3. 一个正方体的每个面都写有一个汉字,其平面展开图如图所示,那么在该正方体中,和“欢”相对的字是( )
 A、英 B、雄 C、凯 D、旋4. 某厂家去年八月份的口罩产量是50万个,十月份的口罩产量是72万个.若设该厂家八月份到十月份的口罩产量的月平均增长率为x , 则下面所列方程正确的是( )A、 B、 C、 D、5. 如图,已知 , 现将A点绕原点O逆时针旋转90°得到 , 则的坐标是( )
A、英 B、雄 C、凯 D、旋4. 某厂家去年八月份的口罩产量是50万个,十月份的口罩产量是72万个.若设该厂家八月份到十月份的口罩产量的月平均增长率为x , 则下面所列方程正确的是( )A、 B、 C、 D、5. 如图,已知 , 现将A点绕原点O逆时针旋转90°得到 , 则的坐标是( ) A、 B、 C、 D、6. 如图,正六边形内接于 , 点在上,则的大小为( )
A、 B、 C、 D、6. 如图,正六边形内接于 , 点在上,则的大小为( ) A、60° B、45° C、30° D、15°7. 如图,在中, , , . 按以下步骤作图:①分别以B、C为圆心,大于为半径作弧,两弧相交于点M和点N;②作直线;③以点D为圆心,的长为半径画圆弧,连接 , 则的长为( )
A、60° B、45° C、30° D、15°7. 如图,在中, , , . 按以下步骤作图:①分别以B、C为圆心,大于为半径作弧,两弧相交于点M和点N;②作直线;③以点D为圆心,的长为半径画圆弧,连接 , 则的长为( )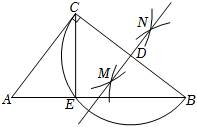 A、 B、 C、 D、8. 如图,在平面直角坐标系中,点 , 都在二次函数的图象上.若 , 则m的取值范围是( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,点 , 都在二次函数的图象上.若 , 则m的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 最简二次根式 与二次根式是同类二次根式,则x= .10. 若关于x的一元二次方程有两个不相等的实数根,则k的值可以是(写出一个即可).11. 正八边形一个外角的大小为度.12. 七巧板起源于我国先秦时期,19世纪传到国外,被称为“唐图”.图①是边长为4的正方形“唐图”,则图②中头部小正方形的面积为 .
 13. 如图,正六边形ABCDEF内接于 . 若的周长为 , 则该正六边形的边长是 .
13. 如图,正六边形ABCDEF内接于 . 若的周长为 , 则该正六边形的边长是 . 14. 如图,在平面直角坐标系中,正方形的点在轴的负半轴上,抛物线的顶点为 , 且经过点、 . 若为等腰直角三角形,则的值是 .
14. 如图,在平面直角坐标系中,正方形的点在轴的负半轴上,抛物线的顶点为 , 且经过点、 . 若为等腰直角三角形,则的值是 .
三、解答题
-
15. 先化简,再求值: , 其中 .16. 有两个不透明的布袋A、B , 分别装有3个小球,布袋A中的小球分别标有数字 , 0,2,布袋B中的小球分别标有数字 , 1,1,它们除数字不同外其他均相同.从布袋A、B中各随机摸出一个小球,用画树状图(或列表)的方法,求摸出的两个小球的数字之和是正数的概率.17. 2022北京冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”深受广大人民的喜爱.2021年十二月,奥林匹克官方旗舰店上架了“冰墩墩”和“雪容融”这两款毛绒玩具,其中“冰墩墩”的销售单价比“雪容融”多40元,当月销售“冰墩墩”的数量是“雪容融”的倍,“雪容融”的销售总额是8000元,“冰墩墩”的销售总额是元.求“雪容融”的销售单价.18. 2022年是中国共产主义青年团建团100周年.某校举办了一次关于共青团知识的竞赛,七、八年级各有300名学生参加了本次活动,为了解两个年级的答题情况,从这两个年级各随机抽取了20名学生的成绩(单位:分)进行调查分析.下面给出了部分信息:
a . 七年级学生的成绩整理如下:
57 69 72 75 76 78 79 80 81 81
83 83 83 85 86 86 88 88 92 96
b . 八年级学生成绩的频数分布直方图如下图.

(数据分成四组: , , , ),其中成绩在的数据如下:
80 82 83 85 85 85 87 88 88 89.
c.两组样本数据的平均数、中位数、众数如下表所示
年级
平均数
中位数
众数
七年级
80.9
82
m
八年级
81.2
n
85
根据所给信息,解答下列问题:
(1)、 , .(2)、根据统计数据,你认为七、八两个年级哪个年级的成绩更好些,请说明理由.(至少从一个角度进行说明)(3)、成绩达到85分及以上为优秀,估计参加本次活动的七年级和八年级学生中,此次测试成绩达到优秀的总人数.19. 图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,在给定的网格中,按照要求作图(保留作图痕迹). (1)、在图①中作△ABC的中线BD .(2)、在图②中作△ABC的高BE .(3)、在图③中作△ABC的角平分线BF .20. 3月23日下午,“天宫课堂”第二课如约举行,某校组织师生全员观看.为了解同学们对“天宫课堂”讲授知识的掌握情况(单位:分)进行了整理、描述和分析.下面给出了相关信息.
(1)、在图①中作△ABC的中线BD .(2)、在图②中作△ABC的高BE .(3)、在图③中作△ABC的角平分线BF .20. 3月23日下午,“天宫课堂”第二课如约举行,某校组织师生全员观看.为了解同学们对“天宫课堂”讲授知识的掌握情况(单位:分)进行了整理、描述和分析.下面给出了相关信息.. 名同学“天宫课堂”知识测试成绩的统计图如下.

.30名同学天宫课堂知识测试成绩的频数分布直方图如下.数据分成6组: , , , , ,

. 测试成绩在这一组的是70,73,73,74,75,75,76,78.
. 小夏同学的“天宫课堂”知识测试成绩为78分.
根据以上信息,回答下列问题:
(1)、小夏同学的测试成绩在抽取的名同学的成绩中从高到低排名第 .(2)、抽取的名同学的成绩的中位数为 .(3)、序号为~的学生是七年级的,序号为~20的学生是八年级的,序号为~的学生是九年级的.若七年级学生成绩的方差记为 , 九年级学生成绩的方差记为 , 则 . (填“”、“”或“”)(4)、成绩分及以上记为优秀,该校初中三个年级名同学都参加测试,估计成绩优秀的同学约为人.21. 缂丝,是中国传统丝绸艺术品中的精华.缂丝织造技艺主要是使用古老的木机(如图①)及若干竹制的梭子和拨子,经过“通经断纬”的织造方法,将五彩的蚕丝线缂织成一幅色彩丰富的织物.缂丝工匠现要完成一件织品,工作一段时间后,记录了工作时间和织品长度的数据变化,并从函数角度进行了如下实验探究.
图①
【数据观察】记录的工作时间x(时)和织品长度y(厘米)的数据变化,如下表:
工作时间x(时)
0
2
4
6
8
织品长度y(厘米)
3
3.6
4.2
4.8
5.4
【探索发现】
(1)、建立平面直角坐标系,如图②,横轴表示记录的工作时间x , 纵轴表示织品长度y , 描出以表格中数据为坐标的各点.
图②
(2)、观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.(3)、如果每天工作10小时,要完成长为240厘米的织品,共需要多少天?22. 如图,是的中线,点是上一点,过点作的平行线,过点作的平行线,两平行线交于点 , 连接 , (1)、【方法感知】如图①,当点与点重合时,易证: . (不需证明)
(1)、【方法感知】如图①,当点与点重合时,易证: . (不需证明)【探究证明】如图②,当点与点不重合时,求证:四边形是平行四边形.
小新同学受到【方法感知】中的启发,经过思考后延长交于点 .
请完成小新同学的证明过程.
(2)、【结论应用】如图③,当 , 时,的延长线交于点 , 且点为中点.=;当时,的长为 .
23. 如图,在矩形中, , .点P从点A出发以每秒2个单位的速度沿运动,到点A停止.在点P运动的同时,点Q从点A出发以每秒1个单位的速度沿运动.当点P回到点A停止时,点Q也随之停止运动.设点P的运动时间为t秒. (1)、用含t的代数式表示线段的长.(2)、以为边作矩形 , 使点M与点A在所在直线的两侧,且.
(1)、用含t的代数式表示线段的长.(2)、以为边作矩形 , 使点M与点A在所在直线的两侧,且.①当点Q在边上,且点M落在上时,求t的值.
②当点M在矩形内部时,直接写出t的取值范围.
(3)、点E在边上,且.在线段上只存在一点F,使 , 直接写出t的取值范围.24. 在平面直角坐标系中,二次函数的图象交x轴于点和点 . (1)、此二次函数的图象与y轴的交点的纵坐标为 .(2)、求此二次函数的关系式.(3)、当时,求二次函数的最大值和最小值.(4)、点P为二次函数图象上任意一点,其横坐标为m,过点P作轴,点Q的横坐标为 . 已知点P与点Q不重合,且线段PQ的长度随m的增大而减小.直接写出线段PQ与二次函数的图象只有1个公共点时m的取值范围.
(1)、此二次函数的图象与y轴的交点的纵坐标为 .(2)、求此二次函数的关系式.(3)、当时,求二次函数的最大值和最小值.(4)、点P为二次函数图象上任意一点,其横坐标为m,过点P作轴,点Q的横坐标为 . 已知点P与点Q不重合,且线段PQ的长度随m的增大而减小.直接写出线段PQ与二次函数的图象只有1个公共点时m的取值范围.