江苏省连云港市2023年中考数学试卷
试卷更新日期:2023-06-17 类型:中考真卷
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
-
1. -6的相反数是( )A、 B、 C、-6 D、62. 在美术字中,有些汉字可以看成是轴对称图形.下列汉字中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2023年4月26日,第十二届江苏园艺博览会在我市隆重开幕,会场所在地园博园分为“山海韵”“丝路情”“田园画”三大片区,共占地约2370000平方米.其中数据“2370000”用科学记数法可表示为( )A、 B、 C、 D、4. 下列水平放置的几何体中,主视图是圆形的是( )A、
3. 2023年4月26日,第十二届江苏园艺博览会在我市隆重开幕,会场所在地园博园分为“山海韵”“丝路情”“田园画”三大片区,共占地约2370000平方米.其中数据“2370000”用科学记数法可表示为( )A、 B、 C、 D、4. 下列水平放置的几何体中,主视图是圆形的是( )A、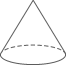 B、
B、 C、
C、 D、
D、 5. 如图,甲是由一条直径、一条弦及一段圆弧所围成的图形;乙是由两条半径与一段圆弧所围成的图形;丙是由不过圆心的两条线段与一段圆弧所围成的图形.下列叙述正确的是( )
5. 如图,甲是由一条直径、一条弦及一段圆弧所围成的图形;乙是由两条半径与一段圆弧所围成的图形;丙是由不过圆心的两条线段与一段圆弧所围成的图形.下列叙述正确的是( ) A、只有甲是扇形 B、只有乙是扇形 C、只有丙是扇形 D、只有乙、丙是扇形6. 如图是由16个相同的小正方形和4个相同的大正方形组成的图形,在这个图形内任取一点 , 则点落在阴影部分的概率为( )
A、只有甲是扇形 B、只有乙是扇形 C、只有丙是扇形 D、只有乙、丙是扇形6. 如图是由16个相同的小正方形和4个相同的大正方形组成的图形,在这个图形内任取一点 , 则点落在阴影部分的概率为( ) A、 B、 C、 D、7. 元朝朱世杰所著的《算学启蒙》中,记载了这样一道题:良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?其大意是:快马每天行240里,慢马每天行150里,慢马先行12天,快马几天可追上慢马?若设快马天可追上慢马,由题意得( )A、 B、 C、 D、8. 如图,矩形内接于 , 分别以为直径向外作半圆.若 , 则阴影部分的面积是( )
A、 B、 C、 D、7. 元朝朱世杰所著的《算学启蒙》中,记载了这样一道题:良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?其大意是:快马每天行240里,慢马每天行150里,慢马先行12天,快马几天可追上慢马?若设快马天可追上慢马,由题意得( )A、 B、 C、 D、8. 如图,矩形内接于 , 分别以为直径向外作半圆.若 , 则阴影部分的面积是( )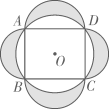 A、 B、 C、 D、20
A、 B、 C、 D、20二、填空题(本大题共8小题,每小题3分,共24分.不需要写出解答过程,请把答案直接填写在答题卡相应位置上)
-
9. 计算:()2=.10. 如图,数轴上的点分别对应实数 , 则0.(用“>”“<”或“=”填空)
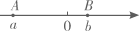 11. 一个三角形的两边长分别是3和5,则第三边长可以是.(只填一个即可)12. 关于的一元二次方程有两个不相等的实数根,则的取值范围是.13. 画一条水平数轴,以原点为圆心,过数轴上的每一刻度点画同心圆,过原点按逆时针方向依次画出与正半轴的角度分别为的射线,这样就建立了“圆”坐标系.如图,在建立的“圆”坐标系内,我们可以将点的坐标分别表示为、 , 则点的坐标可以表示为.
11. 一个三角形的两边长分别是3和5,则第三边长可以是.(只填一个即可)12. 关于的一元二次方程有两个不相等的实数根,则的取值范围是.13. 画一条水平数轴,以原点为圆心,过数轴上的每一刻度点画同心圆,过原点按逆时针方向依次画出与正半轴的角度分别为的射线,这样就建立了“圆”坐标系.如图,在建立的“圆”坐标系内,我们可以将点的坐标分别表示为、 , 则点的坐标可以表示为.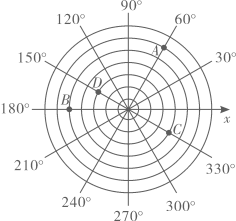 14. 以正六边形的顶点为旋转中心,按顺时针方向旋转,使得新正六边形的顶点落在直线上,则正六边形至少旋转°.
14. 以正六边形的顶点为旋转中心,按顺时针方向旋转,使得新正六边形的顶点落在直线上,则正六边形至少旋转°. 15. 如图,矩形的顶点在反比例函数的图像上,顶点在第一象限,对角线轴,交轴于点.若矩形的面积是 , 则.
15. 如图,矩形的顶点在反比例函数的图像上,顶点在第一象限,对角线轴,交轴于点.若矩形的面积是 , 则. 16. 若(为实数),则的最小值为.
16. 若(为实数),则的最小值为.三、解答题(本大题共11小题,共102分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤,作图过程需保留作图痕迹)
-
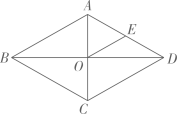
17. 计算.18. 解方程组19. 解方程.20. 如图,菱形的对角线相交于点为的中点, , .求的长及的值.
 21. 为了解本校八年级学生的暑期课外阅读情况,某数学兴趣小组抽取了50名学生进行问卷调查.(1)、下面的抽取方法中,应该选择(____)A、从八年级随机抽取一个班的50名学生 B、从八年级女生中随机抽取50名学生 C、从八年级所有学生中随机抽取50名学生(2)、对调查数据进行整理,得到下列两幅尚不完整的统计图表:
21. 为了解本校八年级学生的暑期课外阅读情况,某数学兴趣小组抽取了50名学生进行问卷调查.(1)、下面的抽取方法中,应该选择(____)A、从八年级随机抽取一个班的50名学生 B、从八年级女生中随机抽取50名学生 C、从八年级所有学生中随机抽取50名学生(2)、对调查数据进行整理,得到下列两幅尚不完整的统计图表:
统计表中的a= , 补全条形统计图;
(3)、若八年级共有800名学生,估计八年级学生暑期课外阅读数量达到2本及以上的学生人数;(4)、根据上述调查情况,写一条你的看法.22. 如图,有4张分别印有Q版西游图案的卡片:A唐僧、B孙悟空、C猪八戒、D沙悟净.
现将这4张卡片(卡片的形状、大小,质地都相同)放在不透明的盒子中,搅匀后从中任意取出1张卡片,记录后放回、搅匀,再从中任意取出1张卡片.求下列事件发生的概率:
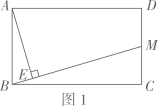
(1)、第一次取出的卡片图案为“B孙悟空”的概率为;(2)、用画树状图或列表的方法,求两次取出的2张卡片中至少有1张图案为“A唐僧”的概率.23. 渔湾是国家“AAAA”级风景区,图1是景区游览的部分示意图.如图2,小卓从九孔桥A处出发,沿着坡角为48°的山坡向上走了92m到达B处的三龙潭瀑布,再沿坡角为37°的山坡向上走了30m到达C处的二龙潭瀑布.求小卓从A处的九孔桥到C处的二龙潭瀑布上升的高度DC为多少米?(结果精确到0.1m)(参考数据:sin48°≈0.74,cos48°≈0.67,sin37°≈0.60,cos37°≈0.80)
 24. 如图,在中, , 以为直径的交边于点 , 连接 , 过点作.
24. 如图,在中, , 以为直径的交边于点 , 连接 , 过点作. (1)、请用无刻度的直尺和圆规作图:过点作的切线,交于点;(不写作法,保留作图痕迹,标明字母)(2)、在(1)的条件下,求证:.25. 目前,我市对市区居民用气户的燃气收费,以户为基础、年为计算周期设定了如下表的三个气量阶梯:
(1)、请用无刻度的直尺和圆规作图:过点作的切线,交于点;(不写作法,保留作图痕迹,标明字母)(2)、在(1)的条件下,求证:.25. 目前,我市对市区居民用气户的燃气收费,以户为基础、年为计算周期设定了如下表的三个气量阶梯:阶梯
年用气量
销售价格
备注
第一阶梯
(含400)的部分
2.67元
若家庭人口超过4人的,每增加1人,第一、二阶梯年用气量的上限分别增加.
第二阶梯
(含1200)的部分
3.15元
第三阶梯
以上的部分
3.63元
(1)、一户家庭人口为3人,年用气量为 , 则该年此户需缴纳燃气费用为元;(2)、一户家庭人口不超过4人,年用气量为 , 该年此户需缴纳燃气费用为元,求与的函数表达式;(3)、甲户家庭人口为3人,乙户家庭人口为5人,某年甲户、乙户缴纳的燃气费用均为3855元,求该年乙户比甲户多用多少立方米的燃气?(结果精确到)26. 如图,在平面直角坐标系中,拋物线的顶点为.直线过点 , 且平行于轴,与拖物线交于(在的右侧).将抛物线沿直线翻折得到抛物线 , 抛物线交轴于点 , 顶点为. (1)、当时,求点的坐标;(2)、连接 , 若为直角三角形,求此时所对应的函数表达式;(3)、在(2)的条件下,若的面积为3,两点分别在边上运动,且 , 以为一边作正方形 , 连接 , 写出长度的最小值,并简要说明理由.27.(1)、【问题情境 建构函数】
(1)、当时,求点的坐标;(2)、连接 , 若为直角三角形,求此时所对应的函数表达式;(3)、在(2)的条件下,若的面积为3,两点分别在边上运动,且 , 以为一边作正方形 , 连接 , 写出长度的最小值,并简要说明理由.27.(1)、【问题情境 建构函数】如图1,在矩形中,是的中点, , 垂足为.设 , 试用含的代数式表示.
 (2)、【由数想形 新知初探】
(2)、【由数想形 新知初探】在上述表达式中,与成函数关系,其图像如图2所示.若取任意实数,此时的函数图象是否具有对称性?若有,请说明理由,并在图2上补全函数图象.
 (3)、【数形结合 深度探究】
(3)、【数形结合 深度探究】在“取任意实数”的条件下,对上述函数继续探究,得出以下结论:①函数值随的增大而增大;②函数值的取值范围是;③存在一条直线与该函数图象有四个交点;④在图像上存在四点 , 使得四边形是平行四边形.其中正确的是.(写出所有正确结论的序号)
(4)、【抽象回归 扩展总结】若将(1)中的“AB=4”改成“”,此时关于的函数表达式是 .一般地,当取任意实数时,类比一次函数、反比例函数、二次函数的研究过程,探究此类函数的相关性质(直接写出3条即可).