吉林省长春市德惠市2023年中考二模数学试卷
试卷更新日期:2023-06-17 类型:中考模拟
一、单选题
-
1. 下列汽车车标中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 截至2021年12月31日,长江干流六座梯级水电站全年累计发电量达2628.83亿千瓦时,相当于减排二氧化碳约2.2亿吨.将262 883 000 000用科学记数法表示应为( )A、 B、 C、 D、3. 实数在数轴上的对应点的位置如图所示,下列结论中正确的是( )
2. 截至2021年12月31日,长江干流六座梯级水电站全年累计发电量达2628.83亿千瓦时,相当于减排二氧化碳约2.2亿吨.将262 883 000 000用科学记数法表示应为( )A、 B、 C、 D、3. 实数在数轴上的对应点的位置如图所示,下列结论中正确的是( ) A、 B、 C、 D、4. 若一个正多边形的一个内角是 , 则这个正多边形的边数为( )A、8 B、7 C、6 D、55. 如图,直线AB∥CD,连接BC,点E是BC上一点, , , 则∠AEC的大小为( )
A、 B、 C、 D、4. 若一个正多边形的一个内角是 , 则这个正多边形的边数为( )A、8 B、7 C、6 D、55. 如图,直线AB∥CD,连接BC,点E是BC上一点, , , 则∠AEC的大小为( )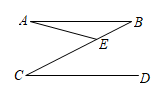 A、27° B、42° C、45° D、70°6. 如图,某飞机于空中A处探测到正下方的地面目标C , 此时飞机高度为1400米,从飞机上看地面控制点B的俯角为 , 则B、C之间的距离为( )
A、27° B、42° C、45° D、70°6. 如图,某飞机于空中A处探测到正下方的地面目标C , 此时飞机高度为1400米,从飞机上看地面控制点B的俯角为 , 则B、C之间的距离为( )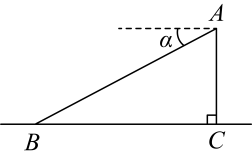 A、米 B、米 C、米 D、米7. 如图,在中, , , 以为圆心,任意长为半径画弧分别交、于点和 , 再分别以、为圆心,大于的长为半径画弧,两弧交于点 , 连接并延长交于点 , 以下结论错误的是( )
A、米 B、米 C、米 D、米7. 如图,在中, , , 以为圆心,任意长为半径画弧分别交、于点和 , 再分别以、为圆心,大于的长为半径画弧,两弧交于点 , 连接并延长交于点 , 以下结论错误的是( ) A、是的平分线 B、 C、点在线段的垂直平分线上 D、8. 在平面直角坐标系 中,点 的图象如图所示,则a的值可以为( )
A、是的平分线 B、 C、点在线段的垂直平分线上 D、8. 在平面直角坐标系 中,点 的图象如图所示,则a的值可以为( ) A、0.7 B、0.9 C、2 D、2.1
A、0.7 B、0.9 C、2 D、2.1二、填空题
-
9. 因式分解: .10. 不等式组的解集是 .11. 如果一个矩形内部能用一些正方形铺满,既不重叠,又无缝隙,就称它为“优美矩形”,如图所示,“优美矩形”的周长为52,则正方形的边长为 .
 12. 将一块含30°角的三角板如图放置,三角板的一个顶点C落在以AB为直径的半圆上,斜边恰好经过点B , 一条直角边与半圆交于点D , 若AB=2,则弧BD的长为(结果保留π).
12. 将一块含30°角的三角板如图放置,三角板的一个顶点C落在以AB为直径的半圆上,斜边恰好经过点B , 一条直角边与半圆交于点D , 若AB=2,则弧BD的长为(结果保留π). 13. 据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示。如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是cm.
13. 据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示。如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是cm. 14. 如图,平面直角坐标系中,直线与x轴、y轴分别交于点C、D , 点A、B为线段的三等分点,且A、B在反比例函数的图象上,若的面积为12,则k的值为 .
14. 如图,平面直角坐标系中,直线与x轴、y轴分别交于点C、D , 点A、B为线段的三等分点,且A、B在反比例函数的图象上,若的面积为12,则k的值为 .
三、解答题
-
15. 先化简,再求值: , 其中 .16. 一只不透明的袋子中装有2个白球、1个红球,这些球除颜色外都相同.(1)、搅匀后从中任意摸出一个球,摸到红球的概率等于;(2)、搅匀后从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出一个球.用列表或画树状图的方法,求2次都摸到红球的概率.17. 某市政工程队承担着1200米长的道路维修任务,为了减少对交通的影响,在维修了240米后通过增加人数和设备提高了工程进度,工作效率是原来的4倍,结果共用了6个小时就完成了任务.求原来每小时维修了多少米?18. 图①,图②,图③均是的正方形网格,每个小正方形的顶点称为格点,线段的端点均在格点上,在图①,图②,图③给定的网格中按要求画图.(保留作图痕迹)
 (1)、在图①中,在线段上画出点 , 使 .(2)、在图②中,画出一个格点 , 使是以为斜边的等腰直角三角形.(3)、在图③中,在线段上画出点 , 使 .19. 如图,点 , 分别在的边 , 上, , 连接 , .请从以下三个条件:①;②;③中,选择一个合适的作为已知条件,使为菱形.
(1)、在图①中,在线段上画出点 , 使 .(2)、在图②中,画出一个格点 , 使是以为斜边的等腰直角三角形.(3)、在图③中,在线段上画出点 , 使 .19. 如图,点 , 分别在的边 , 上, , 连接 , .请从以下三个条件:①;②;③中,选择一个合适的作为已知条件,使为菱形.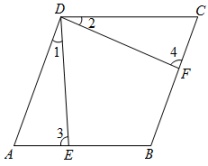 (1)、你添加的条件是(填序号);(2)、添加了条件后,请证明为菱形.20. 某校为引导学生传承红色精神,争当时代新人,在全校开展“红色教育”学习活动,并让学生利用周末的时间,在家观看与“红色教育”相关的视频,为了解学生观看“红色教育”相关视频的时间情况,学校随机调查了部分学生最近一周周末在家观看“红色教育”相关视频的时间,根据调查结果绘制了如下统计图表(均不完整).
(1)、你添加的条件是(填序号);(2)、添加了条件后,请证明为菱形.20. 某校为引导学生传承红色精神,争当时代新人,在全校开展“红色教育”学习活动,并让学生利用周末的时间,在家观看与“红色教育”相关的视频,为了解学生观看“红色教育”相关视频的时间情况,学校随机调查了部分学生最近一周周末在家观看“红色教育”相关视频的时间,根据调查结果绘制了如下统计图表(均不完整).组别
时间/h
频数
频率
A
0~1.0
18
0.12
B
1.0~2.0
45
0.3
C
2.0~3.0
0.4
D
3.0~4.0
27

根据以上信息,解答下列问题:
(1)、共调查了名学生;统计表中, , ;并将条形统计图补充完整;(2)、被调查的学生观看“红色教育”相关视频的时间的中位数在组;(3)、已知A、B、C、D四组数据的平均数分别为0.5,1.5,2.5,3.5,请你估计该校学生最近一周周末观看“红色教育”相关视频的时间的平均数.21. 小林同学从家出发,步行到离家a米的公园散步,速度为50米/分钟:6分钟后哥哥也从家出发沿着同一路线骑自行车到公园,哥哥到达公园后立即以原速返回家中,两人离家的距离y(米)与小林出发的时间x(分钟)的函数关系如图所示. (1)、 ;(2)、求所在直线的函数表达式;(3)、小林与哥哥第二次相遇时距离公园还有多远?22.
(1)、 ;(2)、求所在直线的函数表达式;(3)、小林与哥哥第二次相遇时距离公园还有多远?22. (1)、【自主学习】填空:
(1)、【自主学习】填空:如图1,点是的平分线上一点,点A在上,用圆规在上截取 , 连接 , 可得 , 其理由根据是;
(2)、【理解运用】如图2,在中, , , 平分 , 试判断和、之间的数量关系并写出证明过程.(3)、【拓展延伸】如图3,在中, , , 分别是 , 的平分线, , 交于点 , 若 , , 请直接写出的长.23. 如图,在矩形中, , E为边的中点.点P从点B出发沿射线以每秒2个单位的速度运动,Q为线段的中点.过点P作的垂线,过点Q作的平行线,两线交于点M . 设点P运动的时间为t秒 . (1)、直接写出线段的长.(用含t的代数式表示)(2)、当点M落在边上时,求t的值.(3)、当与矩形重合部分图形为四边形时,求t的取值范围.(4)、当点Q与点M到矩形的一个内角的角平分线距离相等时,直接写出t的值.24. 在平面直角坐标系中,抛物线的对称轴是直线 , 与y轴交点的坐标 .(1)、求抛物线对应的函数表达式.(2)、①当时,y的取值范围是 .
(1)、直接写出线段的长.(用含t的代数式表示)(2)、当点M落在边上时,求t的值.(3)、当与矩形重合部分图形为四边形时,求t的取值范围.(4)、当点Q与点M到矩形的一个内角的角平分线距离相等时,直接写出t的值.24. 在平面直角坐标系中,抛物线的对称轴是直线 , 与y轴交点的坐标 .(1)、求抛物线对应的函数表达式.(2)、①当时,y的取值范围是 .②若时, , 则n的取值范围是 .
(3)、二次函数图象上一点P , 其横坐标为m . 过点P作轴于点Q , 点 , 以、为边构建矩形PQMN , 当矩形的边与二次函数的图象只有三个交点时,直接写出m的取值范围.