吉林省延边州2023年中考一模数学试卷

试卷更新日期：2023-06-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数 $a$ ， $b$ ， $c$ ， $d$ 在数轴上的对应点的位置如图所示，则绝对值最小的数是（）

A、 $a$ B、 $b$ C、 $c$ D、 $d$

查看试题解析
2. $2023$ 年一季度我国生产总值达到了 $28.5$ 亿元，将2850000000用科学记数法表示为（）

A、 $2 .85 \times 10^{9}$ B、 $2 .85 \times 10^{10}$ C、 $28 .5 \times 10^{8}$ D、 $28 .5 \times 10^{9}$

查看试题解析
3. 墨迹覆盖了等式 $a^{6} \div$ $= a^{2}$ 的一部分，则覆盖的部分是（）

A、 $a^{2}$ B、 $a^{4}$ C、 $a^{8}$ D、 $a^{12}$

查看试题解析
4. 把图中的图案绕着它的中心旋转一定角度后与自身重合，则这个旋转角度至少为（）

A、 $60 °$ B、 $90 °$ C、 $120 °$ D、 $180 °$

查看试题解析
5. 如图，AB是⊙O的直径， $\overset{⌢}{A C} = 3 \overset{⌢}{B C}$ ，则∠BAC的度数为（　　）

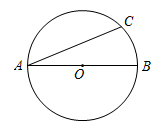A、22.5° B、30° C、45° D、67.5°

查看试题解析
6. 我国元朝数学家朱世杰所著的《算学启蒙》中记载了一道问题，大意是：跑得快的马每天走240里，跑得慢的马每天走150里．慢马先走12天，快马几天可以追上慢马？如果设快马x天可以追上慢马，那么根据题意可列方程为（）

A、 $240 x = 150 (x + 12)$ B、 $240 x = 150 x + 12$ C、 $240 (x - 12) = 150 x$ D、 $240 x = 150 (x - 12)$

查看试题解析

二、填空题

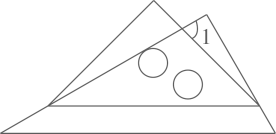
7. 若向北方向记作正数，则先向北走 $200 m$ ，再向南走 $150 m$ ，可以用算式表示为．

查看试题解析
8. 计算： $\sqrt{18} - \sqrt{2}$ = ．

查看试题解析
9. 方程 $\frac{4}{x + 2} = \frac{3}{x + 1}$ 的解是．

查看试题解析
10. 若正n边形一个外角的度数为 $10 °$ ，则n的值为．

查看试题解析
11. 将一副三角尺按如图所示的方式摆放，其中两斜边互相平行，则 $∠ 1$ 的大小为 $°$ ．

查看试题解析
12. 如图， $A B$ 是 $⊙ O$ 的直径， $B C$ 是 $⊙ O$ 的切线，点B为切点，线段 $A C$ 与 $⊙ O$ 交于点D ．点E是 $\overset{⌢}{B D}$ 上的动点（不与点B、D重合）．若 $∠ C = 50 °$ ，则 $∠ B O E$ 的度数可能是 $°$ ．

查看试题解析
13. 如图，矩形 $A B C D$ 中，以B ， D为圆心， $B C ， A D$ 长为半径画弧，分别交对角线 $B D$ 于点E ， F ．若 $A B = 4 ， A D = 4 \sqrt{3}$ ，则图中阴影部分的面积为．（结果保留π）

查看试题解析
14. 平面直角坐标系中，抛物线 $y = a x^{2} + b x + c (a > 0)$ 的对称轴为直线 $x = 1$ ．若点 $P (4 ， y_{1})$ 、 $Q (m ， y_{2})$ 是抛物线上的两点，且 $y_{1} > y_{2}$ ，则m的取值范围是．

查看试题解析

三、解答题

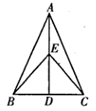
15. 先化简，再求值： $\frac{a - 1}{a} \cdot \frac{a^{2} + 2 a + 1}{a^{2} - 1}$ ，其中 $a = - 2$ ．

查看试题解析
16. 篮球联赛中，每场比赛都要分出胜负，每队胜1场得2分，负1场得1分．某队在10场比赛中得到16分，这个队胜负场数分别是多少?

查看试题解析
17. 一只不透明的袋子中装有1个白球，2个红球，这些球除颜色外都相同．搅匀后从中随机取出1个球，记录颜色后放回．再次搅匀后，从中随机取出1个球．用画树状图（或列表）的方法，求两次取到的球恰好为1个白球和1个红球的概率．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 是 $B C$ 的中点，点 $E$ 在 $A D$ 上，求证： $B E = C E$ ．

查看试题解析
19. 如图是由边长为1的小正方形组成的6×8的正方形网络，每个小正方形的顶点称为格点， $△ A B C$ 的顶点A ， B ， C均在格点上，在给定的网络中，只用无刻度直尺，按要求作图，不要求写画法．

(1)、在图①中，作 $△ D E F$ ，使 $△ D E F ≌ △ A B C$ ，且点D、E、F均在格点上．

(2)、在图②中，作 $△ C G H$ ，使 $△ C G H ∽ △ A B C$ ，点G、H均在格点上，且相似比不为1．

(3)、在图③中，作 $∠ A M B$ ，使 $∠ A M B = 2 ∠ C$ ．

查看试题解析
20. 如图，直线 $y_{1} = k x + b$ 与 $x$ 轴、 $y$ 轴交于点 $A$ 、 $B$ ，与函数 $y_{2} = \frac{m}{x} (x > 0)$ 的图象交于点 $C$ 、 $D$ ．点 $C$ 、 $D$ 恰好是线段 $A B$ 的三等分点，且点 $C$ 的坐标为 $(2 ， 2)$ ．

(1)、求 $m$ 、 $k$ 、 $b$ 的值．

(2)、当 $y_{1} > y_{2}$ 时，直接写出 $x$ 的取值范围．

查看试题解析
21. 如图，斜坡 $A B$ 与地面 $A M$ 的夹角为 $37 °$ ，在斜坡的顶端有一棵竖直的小树 $B C$ ，当太阳光线 $C D$ 与水平线成 $45 °$ 角照射时，在斜坡上形成树影 $B D$ ．已知树影 $B D$ 的长度为 $7 m$ ，求小树 $B C$ 的高．（结果精确到1m）（参考数据： $\sin 37 ° \approx 0.60$ ， $\cos 37 ° \approx 0.80$ ， $\tan 37 ° \approx 0.75$ ）

查看试题解析
22. 我国男性的体质系数计算公式是： $m = \frac{W}{H - 105} \times 100 %$ ，其中W表示体重（单位：kg），H表示身高（单位：cm）．通过计算出的体质系数m对体质进行评价．具体评价如下表：

$m$

$< 80 %$

$80 % ~ 90 %$

$90 % ~ 110 %$

$110 % ~ 120 %$

$> 120 %$

评价结果

明显消瘦

消瘦

正常

过重

肥胖

(1)、某男生的身高是175cm，体重是80kg ，他的体质评价结果是．

(2)、现从某校九年级学生中随机抽取n名男生进行体质评价，评价结果统计如下：
①抽查的学生数n=；图②中a的值为．

②图①中，体质评价结果为“正常”的扇形圆心角为°．

(3)、若该校九年级共有男生450人，试估计该校九年级体质评价结果为“过重”或“肥胖”男生人数的和．

查看试题解析
23. 为增强民众生活幸福感，延吉市政府大力推进城市园林绿化提升工程．计划在 $2000 m^{2}$ 的绿化带上新栽乔木和花卉．市场调查发现：花卉的种植费用为 $150$ 元 ${/m}^{2}$ ，乔木的种植费用 $y$ （元 ${/m}^{2}$ ）与种植面积 $x (m^{2})$ 之间的函数关系如图所示．

(1)、结合图象直接写 $y$ 与 $x$ 的函数关系式，并写出 $x$ 的取值范围．

(2)、当乔木的种植面积不少于 $300 m^{2}$ ，且花卉的种植面积不低于乔木种植面积的 $\frac{1}{3}$ 时，如何分配乔木与花卉的种植面积才能使种植的总费用 $w$ （元）最少？最少是多少元？

查看试题解析
24.

(1)、【探究】
如图①，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ，点 $D$ 是 $A B$ 中点，连接 $C D$ ，则 $A B$ 与 $C D$ 的数量关系是．

(2)、【应用】
如图②，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ，点 $E$ ， $F$ 分别是 $B C$ 、 $C A$ 的中点，连接 $D E$ 、 $D F$ ，且 $D E = 3$ ， $D F = 4$ ，求 $A B$ 的长度．

(3)、【应用】
如图③， $△ A B C$ 的中线 $B D$ 、 $C E$ 相交于点 $O$ ， $F$ 、 $G$ 分别是 $B O$ 、 $CO$ 的中点．连接 $D E$ 、 $E F$ 、 $F G$ 、 $G D$ ．若 $△ A D E$ 的面积为 $6$ ，则四边形 $D E F G$ 的面积为．

查看试题解析
25. 如图，菱形 $A B C D$ 中， $A B = 6 cm ， ∠ B = 60 °$ ．动点P ， Q同时从点A出发，点Q以2cm/s的速度沿折线 $A C - C D$ 向终点D匀速运动，点P以1cm/s的速度沿 $A B$ 向终点B匀速运动．以 $A P 、 A Q$ 为边作平行四边形 $A P M Q$ ．设点P的运动时间为x（s），平行四边形 $A P M Q$ 与 $△ A B C$ 重叠部分图形的面积为y（ ${cm}^{2}$ ）．

(1)、当点Q在边 $A C$ 上运动时，点Q到 $A B$ 的距离为cm．（用含x的代数式表示）

(2)、当点M落在边 $B C$ 上时，x的值为．

(3)、求y关于x的函数解析式，并写出自变量x的取值范围．

查看试题解析
26. 如图，抛物线 $y = - x^{2} + b x + c$ 经过点 $A (- 1 ， 0)$ ，点 $B (3 ， 0)$ ，与y轴交于点C ．点P是抛物线上的动点，且横坐标为m ．过点P作y轴的平行线，交直线 $B C$ 于点Q ，以 $P Q$ 为边，在 $P Q$ 的右侧作正方形 $P Q M N$ ．

(1)、求此抛物线的解析式．

(2)、点P在直线 $B C$ 上方的抛物线上运动时，直接写出 $P Q$ 的长．（用含m的代数式表示）

(3)、抛物线的顶点落在正方形 $P Q M N$ 的边上（包括顶点）时，求m的值．

(4)、当此抛物线在正方形 $P Q M N$ 内部的图象的最高点与最低点的纵坐标之差为2时，直接写出m的值．

查看试题解析

$m$	$< 80 %$	$80 % ~ 90 %$	$90 % ~ 110 %$	$110 % ~ 120 %$	$> 120 %$
评价结果	明显消瘦	消瘦	正常	过重	肥胖