浙江省舟山市2023年中考数学试卷
试卷更新日期:2023-06-17 类型:中考真卷
一、选择题(本题有10小题,每小题3分,共30分,请选出各题中唯一的正确选项,不选、多选,错选,均不得分)
-
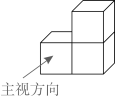
1. -8的立方根是( )A、 B、2 C、 D、不存在2. 如图的几何体由3个同样大小的正方体搭成,它的俯视图是( )
 A、
A、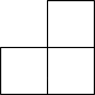 B、
B、 C、
C、 D、
D、 3. 在下面的调查中,最适合用全面调查的是( )A、了解一批节能灯管的使用寿命 B、了解某校803班学生的视力情况 C、了解某省初中生每周上网时长情况 D、了解京杭大运河中鱼的种类4. 美术老师写的下列四个字中,为轴对称图形的是( )A、
3. 在下面的调查中,最适合用全面调查的是( )A、了解一批节能灯管的使用寿命 B、了解某校803班学生的视力情况 C、了解某省初中生每周上网时长情况 D、了解京杭大运河中鱼的种类4. 美术老师写的下列四个字中,为轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,在直角坐标系中,的三个顶点分别为 , 现以原点O为位似中心,在第一象限内作与的位似比为2的位似图形 , 则顶点的坐标是( )
5. 如图,在直角坐标系中,的三个顶点分别为 , 现以原点O为位似中心,在第一象限内作与的位似比为2的位似图形 , 则顶点的坐标是( )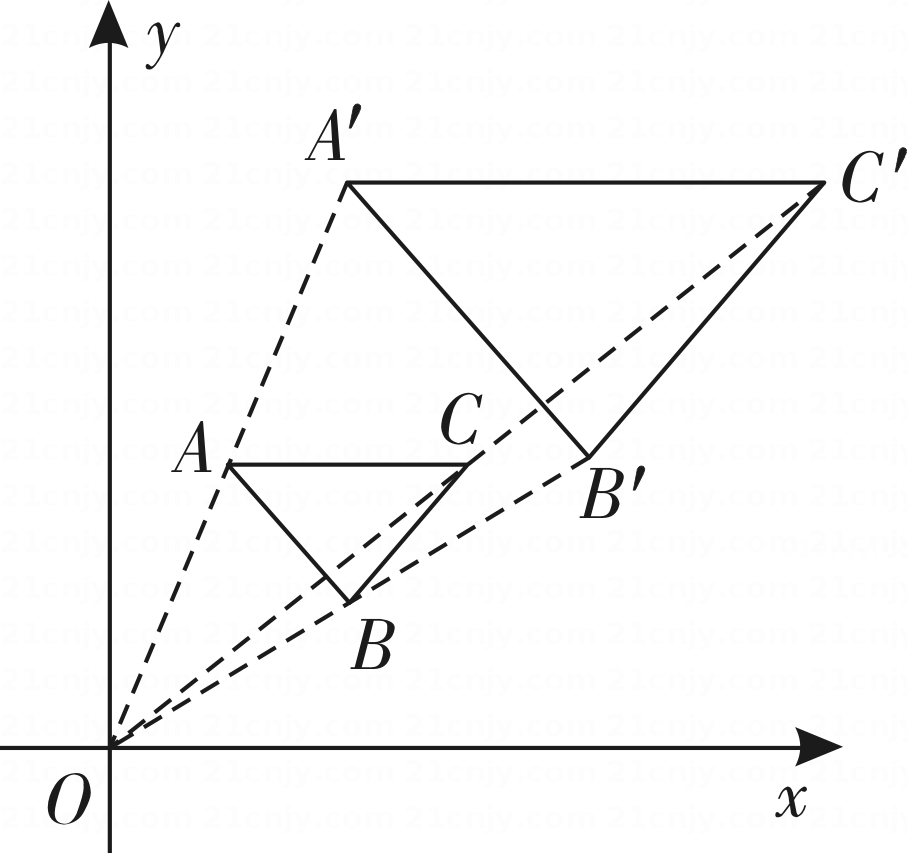 A、 B、 C、 D、6. 下面四个数中,比1小的正无理数是( )A、 B、 C、 D、7. 如图,已知矩形纸片ABCD,其中 , 现将纸片进行如下操作:
A、 B、 C、 D、6. 下面四个数中,比1小的正无理数是( )A、 B、 C、 D、7. 如图,已知矩形纸片ABCD,其中 , 现将纸片进行如下操作:第一步,如图①将纸片对折,使AB与DC重合,折痕为EF,展开后如图②;
第二步,再将图②中的纸片沿对角线BD折叠,展开后如图③;
第三步,将图③中的纸片沿过点E的直线折叠,使点C落在对角线BD上的点H处,如图④.
则DH的长为( ) A、 B、 C、 D、8. 已知点均在反比例函数的图象上,则 , 的大小关系是( )A、 B、 C、 D、9. 如图,点P是的重心,点D是边AC的中点,交BC于点E,交EP于点F,若四边形CDFE的面积为6,则的面积为( )
A、 B、 C、 D、8. 已知点均在反比例函数的图象上,则 , 的大小关系是( )A、 B、 C、 D、9. 如图,点P是的重心,点D是边AC的中点,交BC于点E,交EP于点F,若四边形CDFE的面积为6,则的面积为( ) A、12 B、14 C、18 D、2410. 下图是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是( )
A、12 B、14 C、18 D、2410. 下图是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是( )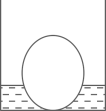 A、
A、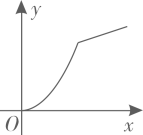 B、
B、 C、
C、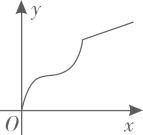 D、
D、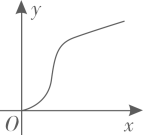
二、填空题(本题有6小题,每小题4分,共24分)
-
11. 计算:。12. 一个多项式,把它因式分解后有一个因式为 , 请你写出一个符合条件的多项式:。13. 现有三张正面印有2023年杭州亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片,卡片除正面图案不同外,其余均相同,将三张卡片正面向下洗匀,从中随机抽取一张卡片,则抽出的卡片图案是琮琮的概率是。
 14. 如图,点A是外一点,AB,AC分别与相切于点B,C,点D在上,已知 , 则的度数是。
14. 如图,点A是外一点,AB,AC分别与相切于点B,C,点D在上,已知 , 则的度数是。 15. 我国古代数学名著《张丘建算经》中有这样一题:一只公鸡值5钱,一只母鸡值3钱,3只小鸡值1钱,现花100钱买了100只鸡.若公鸡有8只,设母鸡有x只,小鸡有y只,可列方程组为。16. 一副三角板ABC和DEF中, . 将它们叠合在一起,边BC与EF重合,CD与AB相交于点G(如图1),此时线段CG的长是 , 现将绕点按顺时针方向旋转(如图2),边EF与AB相交于点H,连结DH,在旋转到的过程中,线段DH扫过的面积是。
15. 我国古代数学名著《张丘建算经》中有这样一题:一只公鸡值5钱,一只母鸡值3钱,3只小鸡值1钱,现花100钱买了100只鸡.若公鸡有8只,设母鸡有x只,小鸡有y只,可列方程组为。16. 一副三角板ABC和DEF中, . 将它们叠合在一起,边BC与EF重合,CD与AB相交于点G(如图1),此时线段CG的长是 , 现将绕点按顺时针方向旋转(如图2),边EF与AB相交于点H,连结DH,在旋转到的过程中,线段DH扫过的面积是。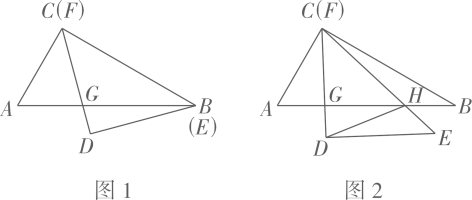
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
-
17.(1)、解不等式: .(2)、已知 , 求的值.18. 小丁和小迪分别解方程过程如下:
小丁:
解:去分母,得
去括号,得
合并同类项,得
解得
∴原方程的解是
小迪:
解:去分母,得
去括号得
合并同类项得
解得
经检验,是方程的增根,原方程无解
你认为小丁和小迪的解法是否正确?若正确,请在框内打“√”;若错误,请在框内打“×”,并写出你的解答过程。
19. 如图,在菱形ABCD中,于点E,于点F,连结EF。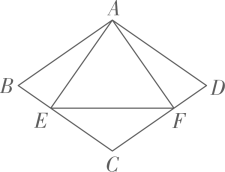 (1)、求证:;(2)、若 , 求的度数。20. 观察下面的等式:(1)、写出的结果.(2)、按上面的规律归纳出一个一般的结论(用含n的等式表示,n为正整数)(3)、请运用有关知识,推理说明这个结论是正确的.21. 小明的爸爸准备购买一辆新能源汽车.在爸爸的预算范围内,小明收集了A,B,C三款汽车在2022年9月至2023年3月期间的国内销售量和网友对车辆的外观造型、舒适程度、操控性能、售后服务等四项评分数据,统计如下:
(1)、求证:;(2)、若 , 求的度数。20. 观察下面的等式:(1)、写出的结果.(2)、按上面的规律归纳出一个一般的结论(用含n的等式表示,n为正整数)(3)、请运用有关知识,推理说明这个结论是正确的.21. 小明的爸爸准备购买一辆新能源汽车.在爸爸的预算范围内,小明收集了A,B,C三款汽车在2022年9月至2023年3月期间的国内销售量和网友对车辆的外观造型、舒适程度、操控性能、售后服务等四项评分数据,统计如下: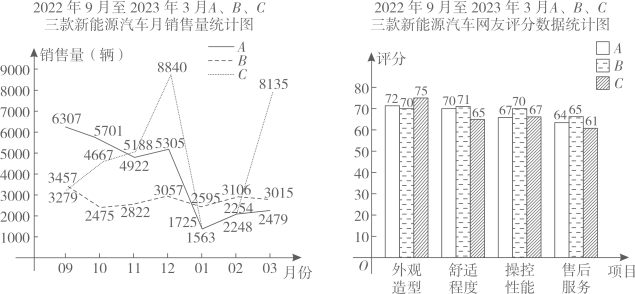 (1)、数据分析:
(1)、数据分析:①求B款新能源汽车在2022年9月至2023年3月期间月销售量的中位数;
②若将车辆的外观造型,舒适程度、操控性能,售后服务等四项评分数据按2:3:3:2的比例统计,求A款新能原汽车四项评分数据的平均数。
(2)、合理建议:请按你认为的各项“重要程度”设计四项评分数据的比例,并结合销售量,以此为依据建议小明的爸爸购买哪款汽车?说说你的理由。
22. 图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,摄像头高度 , 识别的最远水平距离。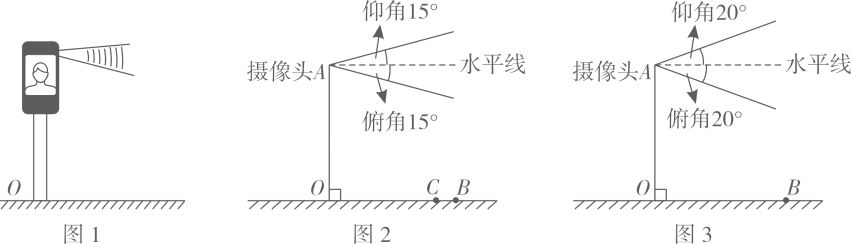 (1)、身高的小杜,头部高度为 , 他站在离摄像头水平距离的点C处,请问小杜最少需要下蹲多少厘米才能被识别。(2)、身高的小若,头部高度为 , 踮起脚尖可以增高 , 但仍无法被识别.社区及时将摄像头的仰角、俯角都调整为(如图3),此时小若能被识别吗?请计算说明。
(1)、身高的小杜,头部高度为 , 他站在离摄像头水平距离的点C处,请问小杜最少需要下蹲多少厘米才能被识别。(2)、身高的小若,头部高度为 , 踮起脚尖可以增高 , 但仍无法被识别.社区及时将摄像头的仰角、俯角都调整为(如图3),此时小若能被识别吗?请计算说明。(精确到 , 参考数据)
23. 在二次函数中,(1)、若它的图象过点 , 则t的值为多少?(2)、当时,y的最小值为 , 求出t的值:(3)、如果都在这个二次函数的图象上,且 , 求m的取值范围。24. 已知,AB是半径为1的的弦,的另一条弦CD满足 , 且于点H(其中点H在圆内,且). (1)、在图1中用尺规作出弦CD与点H(不写作法,保留作图痕迹).(2)、连结AD,猜想,当弦AB的长度发生变化时,线段AD的长度是否变化?若发生变化,说明理由:若不变,求出AD的长度,(3)、如图2,延长AH至点F,使得 , 连结CF,的平分线CP交AD的延长线于点P,点M为AP的中点,连结HM,若 . 求证: .
(1)、在图1中用尺规作出弦CD与点H(不写作法,保留作图痕迹).(2)、连结AD,猜想,当弦AB的长度发生变化时,线段AD的长度是否变化?若发生变化,说明理由:若不变,求出AD的长度,(3)、如图2,延长AH至点F,使得 , 连结CF,的平分线CP交AD的延长线于点P,点M为AP的中点,连结HM,若 . 求证: .