吉林省松原市乾安县2023年中考一模数学试卷
试卷更新日期:2023-06-17 类型:中考模拟
一、单选题
-
1. 直六棱柱如图所示,它的俯视图是( )
 A、
A、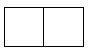 B、
B、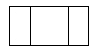 C、
C、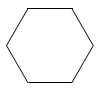 D、
D、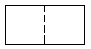 2. 下列计算正确的是( )A、 B、 C、 D、3. 一条古称在称物时的状态如图所示,已知 , 则( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 一条古称在称物时的状态如图所示,已知 , 则( )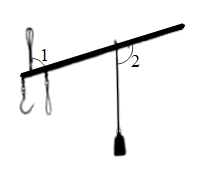 A、 B、 C、 D、4. 如图是小明同学在体育课上跳远后留下的脚印,他的跳远成绩是线段( )的长度,这样测量的依据是( )
A、 B、 C、 D、4. 如图是小明同学在体育课上跳远后留下的脚印,他的跳远成绩是线段( )的长度,这样测量的依据是( )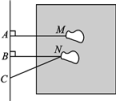 A、 , 两点之间,线段最短 B、 , 两点确定一条直线 C、 , 垂线段最短 D、 , 三角形两边之和大于第三边5. 若关于x的一元二次方程有两个不相等的实数根,则整数k的最小值是( )A、 B、 C、0 D、16. 工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )
A、 , 两点之间,线段最短 B、 , 两点确定一条直线 C、 , 垂线段最短 D、 , 三角形两边之和大于第三边5. 若关于x的一元二次方程有两个不相等的实数根,则整数k的最小值是( )A、 B、 C、0 D、16. 工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( ) A、10cm B、15cm C、20cm D、24cm
A、10cm B、15cm C、20cm D、24cm二、填空题
-
7. 负数的概念最早出现在中国古代著名的数学专著《九章算术》中,负数与对应的正数“数量相等,意义相反”,如果向东走了5米,记作+5米,那么向西走5米,可记作米.8. 2023年全国两会在北京圆满落下帷幕.《两会微博热度报告》显示,两会相关话题信息阅读量达78200000000.数据78200000000用科学记数法表示为 .9. 计算:2cos60°= .10. 分解因式: .11. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“美学”,如图, , 这个比值介于整数和之间,则的值是 .
 12. 反比例函数的图象经过、两点,当时, , 写出符合条件的的值(答案不唯一,写出一个即可).13. 如图,为了测量山坡的护坡石坝高,把一根长为 的竹竿 斜靠在石坝旁,量出竿上 长为 时,它离地面的高度 为 ,则坝高 为 .
12. 反比例函数的图象经过、两点,当时, , 写出符合条件的的值(答案不唯一,写出一个即可).13. 如图,为了测量山坡的护坡石坝高,把一根长为 的竹竿 斜靠在石坝旁,量出竿上 长为 时,它离地面的高度 为 ,则坝高 为 . 14. 如图,在中, , , 将绕点逆时针旋转 , 得到 , 连接并延长交于点 , 当时,的长是 .
14. 如图,在中, , , 将绕点逆时针旋转 , 得到 , 连接并延长交于点 , 当时,的长是 .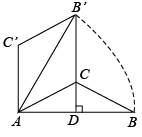
三、解答题
-
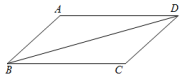
15. 先化简,再求值:﹣ , 其中a=3.16. 如图,在中,是它的一条对角线,求证: .
 17. 孟浩然是唐代著名的山水田园派诗人.《春晓》是他创作的一首名篇,这首古诗共有四句,如图,将这四句古诗分别制成编号为A,B,C,D的4张卡片,卡片除编号和内容外,其余完全相同.将这4张卡片背面朝上,洗匀放好.现从4张卡片中随机抽取2张,请用列表或画树状图的方法,求出随机抽出2张卡片恰好为相邻两句古诗的概率.
17. 孟浩然是唐代著名的山水田园派诗人.《春晓》是他创作的一首名篇,这首古诗共有四句,如图,将这四句古诗分别制成编号为A,B,C,D的4张卡片,卡片除编号和内容外,其余完全相同.将这4张卡片背面朝上,洗匀放好.现从4张卡片中随机抽取2张,请用列表或画树状图的方法,求出随机抽出2张卡片恰好为相邻两句古诗的概率.A.
 B.
B.
C.
 D.
D. 18. 图①、图②、图③均是5×5的正方形网格,每个小正方形的边长均为1,其顶点称为格点,△ABC的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
18. 图①、图②、图③均是5×5的正方形网格,每个小正方形的边长均为1,其顶点称为格点,△ABC的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.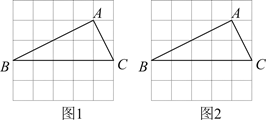 (1)、网格中的形状是;(2)、在图①中确定一点D . 连结、 , 使与全等;(3)、在图②中的边上确定一点E , 连结 , 使 .19. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜元,某商家用元购进的猪肉粽和用元购进的豆沙粽盒数相同.求猪肉粽和豆沙粽每盒的进价.20. 综合与实践
(1)、网格中的形状是;(2)、在图①中确定一点D . 连结、 , 使与全等;(3)、在图②中的边上确定一点E , 连结 , 使 .19. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜元,某商家用元购进的猪肉粽和用元购进的豆沙粽盒数相同.求猪肉粽和豆沙粽每盒的进价.20. 综合与实践【问题情境】数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动,
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片,通过测量得到这些树叶的长y(单位:cm),宽x(单位:cm)的数据后,分别计算长宽比,整理数据如下:
1
2
3
4
5
6
7
8
9
10
芒果树叶的长宽比
3.8
3.7
3.5
3.4
3.8
4.0
3.6
4.0
3.6
4.0
荔枝树叶的长宽比
2.0
2.0
2.0
2.4
1.8
1.9
1.8
2.0
1.3
1.9
【实践探究】分析数据如下:

平均数
中位数
众数
方差
芒果树叶的长宽比
3.74
m
4.0
0.0424
荔枝树叶的长宽比
1.91
2.0
n
0.0669
【问题解决】
(1)、上述表格中, , ;(2)、①A同学说:“从树叶的长宽比的方差来看,我认为芒果树叶的形状差别大.”②B同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的两倍.”
上面两位同学的说法中,合理的是(填序号)
(3)、现有一片长 , 宽的树叶,请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由.21. 今年,我国“巅峰使命”2022珠峰科考团对珠穆朗玛峰进行综合科学考察,搭建了世界最高海拔的自动气象站,还通过释放气球方式进行了高空探测.某学校兴趣小组开展实践活动,通过观测数据,计算气球升空的高度AB.如图,在平面内,点B,C,D在同一直线上, 垂足为点B, , , ,求AB的高度.(精确到 )(参考数据: ﹐ ﹐ , )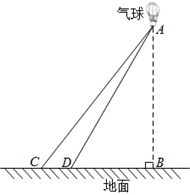 22. 某种机器工作前先将空油箱加满,然后停止加油立即开始工作,当停止工作时,油箱中油量为 .在整个过程中,油箱里的油量y(单位:L)与时间x(单位: )之间的关系如图所示.
22. 某种机器工作前先将空油箱加满,然后停止加油立即开始工作,当停止工作时,油箱中油量为 .在整个过程中,油箱里的油量y(单位:L)与时间x(单位: )之间的关系如图所示.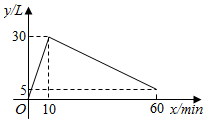 (1)、机器每分钟加油量为L,机器工作的过程中每分钟耗油量为L.(2)、求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.(3)、直接写出油箱中油量为油箱容积的一半时x的值.23. 综合与实践
(1)、机器每分钟加油量为L,机器工作的过程中每分钟耗油量为L.(2)、求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.(3)、直接写出油箱中油量为油箱容积的一半时x的值.23. 综合与实践综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
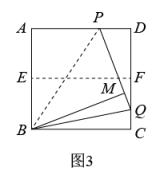
 (1)、操作判断
(1)、操作判断操作一:对折矩形纸片ABCD , 使AD与BC重合,得到折痕EF , 把纸片展平;
操作二:在AD上选一点P , 沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM , BM .
根据以上操作,当点M在EF上时,写出图1中一个30°的角: .
(2)、迁移探究小华将矩形纸片换成正方形纸片,继续探究,过程如下:
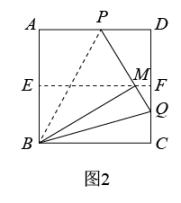
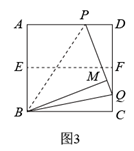
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q , 连接BQ .
①如图2,当点M在EF上时,∠MBQ= ▲ , ∠CBQ= ▲ °;
②改变点P在AD上的位置(点P不与点A , D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)、拓展应用在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.
24. 如图,在△ABC中,∠C=90°,AC=BC=4,P,Q两点同时从C出发,点P 以每秒2个单位长度的速度沿CB向终点B运动;点Q 以每秒1个单位长度的速度沿CA向终点A运动,以CP,CQ为邻边作矩形CPMQ.当点P停止运动时,点Q继续向终点A运动.设点Q的运动时间为t秒.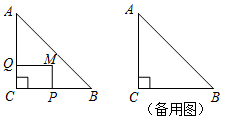 (1)、在点P的运动过程中,CQ= , BP=(用含t的代数式表示);(2)、当点M落在AB边上时,t =s;(3)、设矩形CPMQ与△ABC重合部分图形的面积为S,求S与t之间的函数关系式;25. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象经过点A(0,-4),点B(4,0).
(1)、在点P的运动过程中,CQ= , BP=(用含t的代数式表示);(2)、当点M落在AB边上时,t =s;(3)、设矩形CPMQ与△ABC重合部分图形的面积为S,求S与t之间的函数关系式;25. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象经过点A(0,-4),点B(4,0).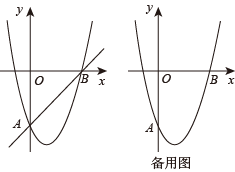 (1)、求此二次函数的解析式.(2)、若点P是直线AB下方抛物线上一动点,当△PAB的面积最大时,求出点P的坐标和△PAB的最大面积.(3)、当t≤x≤t+3时,此二次函数的最大值为m , 最小值为n , 若m-n=3,直接写出t的值.
(1)、求此二次函数的解析式.(2)、若点P是直线AB下方抛物线上一动点,当△PAB的面积最大时,求出点P的坐标和△PAB的最大面积.(3)、当t≤x≤t+3时,此二次函数的最大值为m , 最小值为n , 若m-n=3,直接写出t的值.