吉林省松原市前郭县西部学区2023年中考一模数学试卷
试卷更新日期:2023-06-17 类型:中考模拟
一、单选题
-
1. 下列计算结果为5的是( )A、 B、 C、 D、2. 是某三角形三边的长,则 等于( )A、 B、 C、10 D、43. 下列四幅图片上呈见的是垃圾类型及标识图案,其中标识图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 不等式3x+1<2x的解在数轴上表示正确的是( )A、
4. 不等式3x+1<2x的解在数轴上表示正确的是( )A、 B、
B、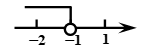 C、
C、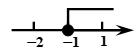 D、
D、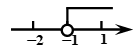 5. 将含30°角的一个直角三角板和一把直尺如图放置,若 ,则 等于( )
5. 将含30°角的一个直角三角板和一把直尺如图放置,若 ,则 等于( )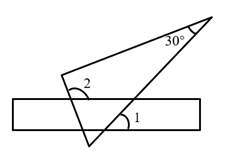 A、80° B、100° C、110° D、120°6. 如图,圆柱的底面直径为AB,高为AC.一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A、80° B、100° C、110° D、120°6. 如图,圆柱的底面直径为AB,高为AC.一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )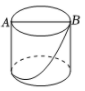 A、
A、 B、
B、 C、
C、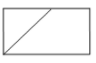 D、
D、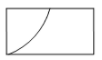
二、填空题
-
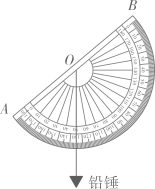
7. 分解因式: .8. 为了解某校学生对湖南省“强省会战略”的知晓情况,从该校全体1000名学生中,随机抽取了100名学生进行调查.结果显示有95名学生知晓.由此,估计该校全体学生中知晓湖南省“强省会战略”的学生有名.9. 已知 ,则 .10. 若关于x的一元二次方程 有两个不相等的实数根,则点 在第象限.11. 如图,在量角器的圆心O处下挂一铅锤,制作了一个简易测倾仪.量角器的0刻度线AB对准楼顶时,铅垂线对应的读数是50°,则此时观察楼顶的仰角度数是 .
 12. 第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素.如图,这个图案绕着它的中心旋转角后能够与它本身重合,则角可以为度.(写出一个即可)
12. 第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素.如图,这个图案绕着它的中心旋转角后能够与它本身重合,则角可以为度.(写出一个即可)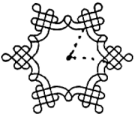 13. 已知二元一次方程组 , 则的值为.14. 如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为 ,则半圆的半径OA的长为 .
13. 已知二元一次方程组 , 则的值为.14. 如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为 ,则半圆的半径OA的长为 .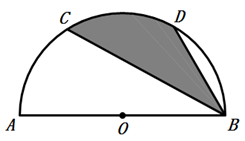
三、解答题
-
15. 解不等式组请按下列步骤完成解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来:
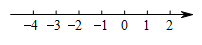 (4)、原不等式组的解集是.16. 学校师生去距学校45千米的吴玉章故居开展研学活动,骑行爱好者张老师骑自行车先行2小时后,其余师生乘汽车出发,结果同时到达;已知汽车速度是自行车速度的3倍,求张老师骑车的速度.17. 如图,在△ABC中,点D在边BC上,CD=AB,DE∥AB,∠DCE=∠A.求证:DE=BC.
(4)、原不等式组的解集是.16. 学校师生去距学校45千米的吴玉章故居开展研学活动,骑行爱好者张老师骑自行车先行2小时后,其余师生乘汽车出发,结果同时到达;已知汽车速度是自行车速度的3倍,求张老师骑车的速度.17. 如图,在△ABC中,点D在边BC上,CD=AB,DE∥AB,∠DCE=∠A.求证:DE=BC.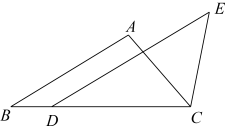 18. 甲、乙两名同学玩一个游戏:在一个不透明的口袋中装有标号分别为1,2,3,4的四个小球(除标号外无其它差异).从口袋中随机摸出一个小球,记下标号后放回口袋中,充分摇匀后,再从口袋中随机摸出一个小球,记下该小球的标号,两次记下的标号分别用x、y表示.若x+y为奇数,则甲获胜;若x+y为偶数,则乙获胜.(1)、用列表法或树状图法(树状图也称树形图)中的一种方法,求(x,y)所有可能出现的结果总数;(2)、你认为这个游戏对双方公平吗?请说明理由.19. 如图,已知正比例函数与反比例函数的图象交于 , 两点.
18. 甲、乙两名同学玩一个游戏:在一个不透明的口袋中装有标号分别为1,2,3,4的四个小球(除标号外无其它差异).从口袋中随机摸出一个小球,记下标号后放回口袋中,充分摇匀后,再从口袋中随机摸出一个小球,记下该小球的标号,两次记下的标号分别用x、y表示.若x+y为奇数,则甲获胜;若x+y为偶数,则乙获胜.(1)、用列表法或树状图法(树状图也称树形图)中的一种方法,求(x,y)所有可能出现的结果总数;(2)、你认为这个游戏对双方公平吗?请说明理由.19. 如图,已知正比例函数与反比例函数的图象交于 , 两点.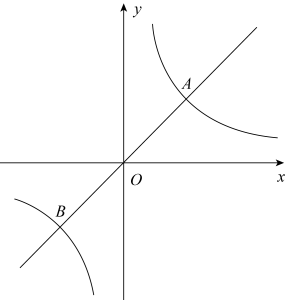 (1)、求的解析式并直接写出时的取值范围;(2)、以为一条对角线作菱形,它的周长为 , 在此菱形的四条边中任选一条,求其所在直线的解析式.20. 如图,在的方格纸中,已知格点P , 请按要求画格点图形(顶点均在格点上).
(1)、求的解析式并直接写出时的取值范围;(2)、以为一条对角线作菱形,它的周长为 , 在此菱形的四条边中任选一条,求其所在直线的解析式.20. 如图,在的方格纸中,已知格点P , 请按要求画格点图形(顶点均在格点上). (1)、在图1中画一个锐角三角形,使P为其中一边的中点,再画出该三角形向右平移2个单位后的图形.(2)、在图2中画一个以P为一个顶点的钝角三角形,使三边长都不相等,再画出该三角形绕点P旋转后的图形.21. 随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量广场 两点之间的距离.如图所示,小星站在广场的 处遥控无人机,无人机在 处距离地面的飞行高度是 ,此时从无人机测得广场 处的俯角为 ,他抬头仰视无人机时,仰角为 ,若小星的身高 (点 在同一平面内).
(1)、在图1中画一个锐角三角形,使P为其中一边的中点,再画出该三角形向右平移2个单位后的图形.(2)、在图2中画一个以P为一个顶点的钝角三角形,使三边长都不相等,再画出该三角形绕点P旋转后的图形.21. 随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量广场 两点之间的距离.如图所示,小星站在广场的 处遥控无人机,无人机在 处距离地面的飞行高度是 ,此时从无人机测得广场 处的俯角为 ,他抬头仰视无人机时,仰角为 ,若小星的身高 (点 在同一平面内).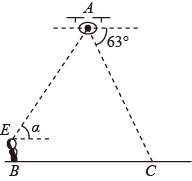 (1)、求仰角 的正弦值;(2)、求 两点之间的距离(结果精确到 ).22. 某兴趣小组随机调查了某市50名教师某日行走的步数情况并进行了统计整理,绘制了如下的统计图表(不完整):
(1)、求仰角 的正弦值;(2)、求 两点之间的距离(结果精确到 ).22. 某兴趣小组随机调查了某市50名教师某日行走的步数情况并进行了统计整理,绘制了如下的统计图表(不完整):步数/步
频数
频率
8
15
12
3
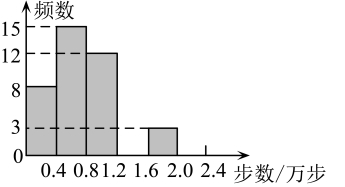
请根据以上信息,解答下列问题:
(1)、写出 , , , 的值并补全频数分布直方图;(2)、该市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?23. 随着“公园城市”建设的不断推进,成都绕城绿道化身成为这座城市的一个超大型“体育场”,绿道骑行成为市民的一种低碳生活新风尚.甲、乙两人相约同时从绿道某地出发同向骑行,甲骑行的速度是 , 乙骑行的路程与骑行的时间之间的关系如图所示.
 (1)、直接写出当和时,与之间的函数表达式;(2)、何时乙骑行在甲的前面?24. 已知:如图,四边形ABCD,AB∥DC,CB⊥AB,AB=16cm,BC=6cm,CD=8cm,动点P从点D开始沿DA边匀速运动,动点Q从点A开始沿AB边匀速运动,它们的运动速度均为2cm/s.点P和点Q同时出发,以QA、QP为边作平行四边形AQPE,设运动的时间为t(s),0<t<5.
(1)、直接写出当和时,与之间的函数表达式;(2)、何时乙骑行在甲的前面?24. 已知:如图,四边形ABCD,AB∥DC,CB⊥AB,AB=16cm,BC=6cm,CD=8cm,动点P从点D开始沿DA边匀速运动,动点Q从点A开始沿AB边匀速运动,它们的运动速度均为2cm/s.点P和点Q同时出发,以QA、QP为边作平行四边形AQPE,设运动的时间为t(s),0<t<5.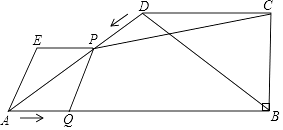
根据题意解答下列问题:
(1)、用含t的代数式表示AP;(2)、设四边形CPQB的面积为S(cm2),求S与t的函数关系式;
(3)、当QP⊥BD时,求t的值;
(4)、在运动过程中,是否存在某一时刻t,使点E在∠ABD的平分线上?若存在,求出t的值;若不存在,请说明理由.
25. 问题背景:一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论.如图1,已知AD是△ABC的角平分线,可证=.小慧的证明思路是:如图2,过点C作CE∥AB,交AD的延长线于点E,构造相似三角形来证明=.
 (1)、尝试证明:请参照小慧提供的思路,利用图2证明=;(2)、应用拓展:如图3,在Rt△ABC中,∠BAC=90°,D是边BC上一点.连接AD,将△ACD沿AD所在直线折叠,点C恰好落在边AB上的E点处.
(1)、尝试证明:请参照小慧提供的思路,利用图2证明=;(2)、应用拓展:如图3,在Rt△ABC中,∠BAC=90°,D是边BC上一点.连接AD,将△ACD沿AD所在直线折叠,点C恰好落在边AB上的E点处.①若AC=1,AB=2,求DE的长;
②若BC=m,∠AED= , 求DE的长(用含m,的式子表示).
26. 已知二次函数 .(1)、求二次函数图象的顶点坐标;(2)、当时,函数的最大值和最小值分别为多少?(3)、当时,函数的最大值为 , 最小值为 , m-n=3求的值.