吉林省松原市前郭县南部学区2023年中考一模数学试卷
试卷更新日期:2023-06-17 类型:中考模拟
一、单选题
-
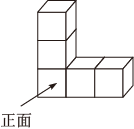
1. 下列4个实数中,为无理数的是( )A、-2 B、0 C、 D、3.142. 图是由5个相同的小正方体组合而成的立体图形,其主视图是( )
 A、
A、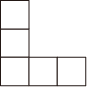 B、
B、 C、
C、 D、
D、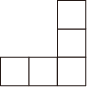 3. 不等式的解集是( )A、 B、 C、 D、4. 如图,数轴上的点P表示下列四个无理数中的一个,这个无理数是( )
3. 不等式的解集是( )A、 B、 C、 D、4. 如图,数轴上的点P表示下列四个无理数中的一个,这个无理数是( )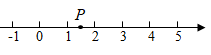 A、 B、 C、 D、π5. 如图,在中,根据尺规作图痕迹,下列说法不一定正确的是( )
A、 B、 C、 D、π5. 如图,在中,根据尺规作图痕迹,下列说法不一定正确的是( ) A、 B、 C、 D、6. 如图,四边形是的内接四边形.若 , 则的度数为( )
A、 B、 C、 D、6. 如图,四边形是的内接四边形.若 , 则的度数为( )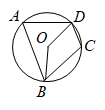 A、138° B、121° C、118° D、112°
A、138° B、121° C、118° D、112°二、填空题
-
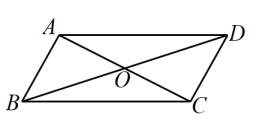
7. 据统计,2022届高校毕业生规模预计首次突破千万,约为10760000 人,总量和增量均为近年之最.将10760000用科学记数法表示为 .8. 分解因式x3+6x2+9x= .9. 已知 是一元二次方程 的一个根,则代数式 的值等于 .10. 一个正多边形的每个外角为60°,那么这个正多边形的内角和是。11. 我国古代著作《增删算法统宗》中记载了一首古算诗:“林下牧童闹如簇,不知人数不知竹每人六竿多十四,每人八竿恰齐足”其大意是:“牧童们在树下拿着竹竿高兴地玩耍,不知与多少人和竹竿每人6竿,多14竿;每人8竿,恰好用完”若设有牧童x人,根据题意,可列方程为 .12. 如图,在中,AD=10,对角线AC与BD相交于点O , AC+BD=22,则△BOC的周长为
 13. 在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,若AE=2,△ADE的面积为4,四边形BCED的面积为5,则边AB的长为 .
13. 在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,若AE=2,△ADE的面积为4,四边形BCED的面积为5,则边AB的长为 .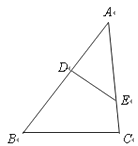 14. 如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B.若 , 则k= .
14. 如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B.若 , 则k= .
三、解答题
-
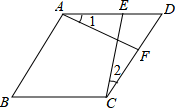
15. 先化简,再求值: , 其中 .16. 某校合唱团为了开展线上“百人合唱一首歌”的“云演出”活动,需招收新成员,小贤、小晴、小艺、小志四名同学报名参加了应聘活动,其中小贤、小艺来自七年级,小志、小晴来自八年级,现对这四名同学采取随机抽取的方式进行线上面试.(1)、若随机抽取一名同学,恰好抽到小艺同学的概率为;(2)、若随机抽取两名同学,请用列表法或树状图法求两名同学均来自八年级的概率.17. 如图,在菱形ABCD中,点E、F分别为AD、CD边上的点,DE=DF , 求证:∠1=∠2.
 18. 为了让学生崇尚劳动,尊重劳动,在劳动中提升综合素质,某校定期开展劳动实践活动.甲、乙两班在一次体验挖土豆的活动中,甲班挖1500千克土豆与乙班挖1200千克土豆所用的时间相同.已知甲班平均每小时比乙班多挖100千克土豆,问乙班平均每小时挖多少千克土豆?19. 如图,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.
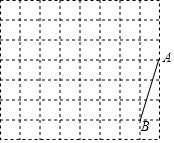
18. 为了让学生崇尚劳动,尊重劳动,在劳动中提升综合素质,某校定期开展劳动实践活动.甲、乙两班在一次体验挖土豆的活动中,甲班挖1500千克土豆与乙班挖1200千克土豆所用的时间相同.已知甲班平均每小时比乙班多挖100千克土豆,问乙班平均每小时挖多少千克土豆?19. 如图,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.⑴在图中画出以线段AB为一边的矩形ABCD(不是正方形),且点C和点D均在小正方形的顶点上;
⑵在图中画出以线段AB为一腰,底边长为2的等腰三角形ABE,点E在小正方形的顶点上,连接CE,请直接写出线段CE的长.
 20. 如图,B,C是反比例函数y= (k≠0)在第一象限图象上的点,过点B的直线y=x-1与x轴交于点A,CD⊥x轴,垂足为D,CD与AB交于点E,OA=AD,CD=3.
20. 如图,B,C是反比例函数y= (k≠0)在第一象限图象上的点,过点B的直线y=x-1与x轴交于点A,CD⊥x轴,垂足为D,CD与AB交于点E,OA=AD,CD=3.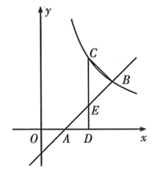 (1)、求此反比例函数的表达式;(2)、求△BCE的面积.21. 某综合与实践研究小组根据我国第七次人口普查数据进行整理、描述和分析,给出部分数据信息:
(1)、求此反比例函数的表达式;(2)、求△BCE的面积.21. 某综合与实践研究小组根据我国第七次人口普查数据进行整理、描述和分析,给出部分数据信息:信息一:普查登记的全国大陆31个省、自治区、直辖市人口数的频数分布直方图如下:
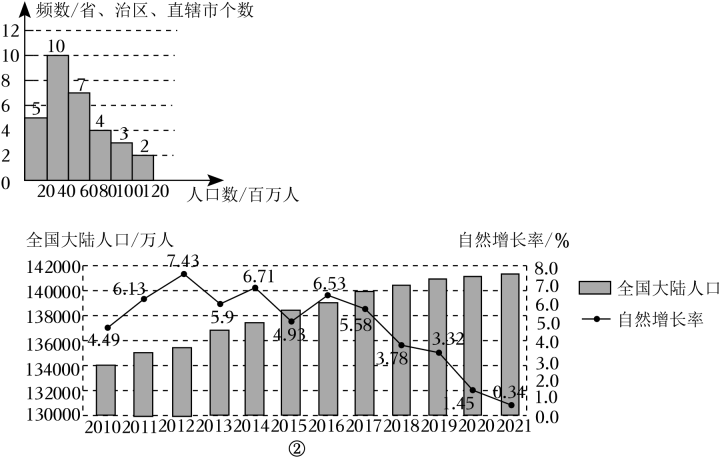
(数据分成6组: , , , , , )
信息二:普查登记的全国大陆31个省、自治区、直辖市人口数(百万人)在这一组的数据是:58,47,45,40,43,42,50;
信息三:年全国大陆人口数及自然增长率;
请根据以上信息,解答下列问题:
(1)、普查登记的全国大陆31个省、自治区、直辖市人口数的中位数为百万人;(2)、下列结论正确的是 . (只填序号)①全国大陆31个省、自治区、直辖市中人口数大于等于100(百万人)的有2个;
②相对于2020年,2021年全国大陆人口自然增长率降低,全国大陆人口增长缓慢;
③年全国大陆人口自然增长率持续降低.
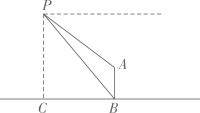
(3)、请写出年全国大陆人口数、全国大陆人口自然增长率的变化趋势,结合变化趋势谈谈自己的看法.22. 如图,一个热气球悬停在空中,从热气球上的P点测得直立于地面的旗杆AB的顶端A与底端B的俯角分别为34°和45°,此时P点距地面高度PC为75米,求旗杆AB的高度(结果精确到0.1米).(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67)
 23. 在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
23. 在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题: (1)、求乙队在2≤x≤6的时段内,y与x之间的函数关系式;(2)、如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?24. 综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点, ,EP与正方形的外角 的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;
(1)、求乙队在2≤x≤6的时段内,y与x之间的函数关系式;(2)、如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?24. 综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点, ,EP与正方形的外角 的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;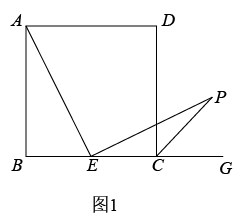
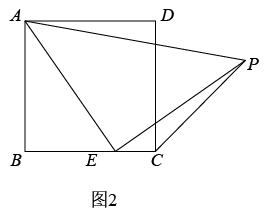
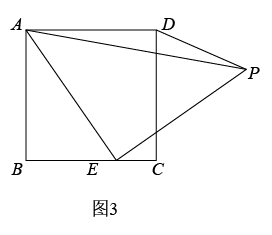 (1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.25. 如图,四边形 为矩形, , ,P、Q均从点B出发,点P以2个单位每秒的速度沿 的方向运动,点Q以1个单位每秒的速度沿 运动,设运动时间为t秒.
(1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.25. 如图,四边形 为矩形, , ,P、Q均从点B出发,点P以2个单位每秒的速度沿 的方向运动,点Q以1个单位每秒的速度沿 运动,设运动时间为t秒.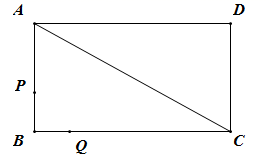 (1)、求 的长;(2)、若 ,求S关于t的解析式.26. 抛物线y=x2-4x与直线y=x交于原点O和点B,与x轴交于另一点A,顶点为D.
(1)、求 的长;(2)、若 ,求S关于t的解析式.26. 抛物线y=x2-4x与直线y=x交于原点O和点B,与x轴交于另一点A,顶点为D.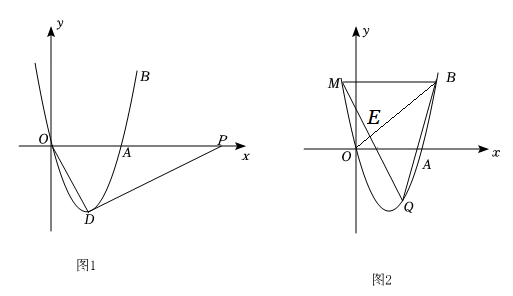 (1)、直接写出点B和点D的坐标;(2)、如图1,连接OD,P为x轴上的动点,当tan∠PDO=时,求点P的坐标;(3)、如图2,M是点B关于抛物线对称轴的对称点,Q是抛物线上的动点,它的横坐标为m(0<m<5),连接MQ,BQ,MQ与直线OB交于点E.设△BEQ和△BEM的面积分别为S1和S2 , 求的最大值.
(1)、直接写出点B和点D的坐标;(2)、如图1,连接OD,P为x轴上的动点,当tan∠PDO=时,求点P的坐标;(3)、如图2,M是点B关于抛物线对称轴的对称点,Q是抛物线上的动点,它的横坐标为m(0<m<5),连接MQ,BQ,MQ与直线OB交于点E.设△BEQ和△BEM的面积分别为S1和S2 , 求的最大值.