吉林省白城市洮北区2023年中考一模数学试卷
试卷更新日期:2023-06-17 类型:中考模拟
一、单选题
-
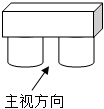
1. 四个数﹣3,0,1,2,其中负数是( )A、﹣3 B、0 C、1 D、22. 预计到2025年,中国5G用户将超过460000000,将460000000用科学记数法表示为( )A、4.6×109 B、46×107 C、4.6×108 D、0.46×1093. 不等式3x+1<10的解集是( )A、x>4 B、x>3 C、x<4 D、x<34. 石鼓广场供游客休息的石板凳如图所示,它的主视图是( )
 A、
A、
B、
B、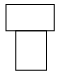 C、
C、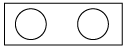 D、
D、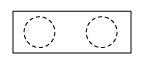 5. 计算的结果( )A、 B、 C、 D、6. 如图,四边形为的内接四边形,若 , 则等于( )
5. 计算的结果( )A、 B、 C、 D、6. 如图,四边形为的内接四边形,若 , 则等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 计算: .8. 分解因式 .9. 关于x的方程的解是.10. 若关于x的一元二次方程有两个不相等的实数根,则k的值可以是(写出一个即可).11. 在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为米.12. 如图,以点O为圆心,以OP的长为半径画弧,交x轴的正半轴与点A . 则点A的坐标为( , 0),P点的纵坐标为-1,则P点的坐标为 .
 13. 如图,四边形是平行四边形,以点B为圆心,的长为半径作弧交于点E,分别以点C,E为圆心、大于的长为半径作弧,两弧交于点P,作射线交的延长线于点F, , 则的长为 .
13. 如图,四边形是平行四边形,以点B为圆心,的长为半径作弧交于点E,分别以点C,E为圆心、大于的长为半径作弧,两弧交于点P,作射线交的延长线于点F, , 则的长为 . 14. 如图,在扇形中,半径的长为2,点在弧上,连接 , , , 若四边形为菱形,则图中阴影部分的面积为 . (用含的代数式表示)
14. 如图,在扇形中,半径的长为2,点在弧上,连接 , , , 若四边形为菱形,则图中阴影部分的面积为 . (用含的代数式表示)
三、解答题
-
15. 先化简,再求值: , 其中 .16. 2022年北京冬奥会期间,小李同学手工制作了三张带有图案的不透明A、B、C卡片(其中A代表短道速滑;B代表花样滑冰;C代表速度滑冰),卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再随机抽取一张,请用画树状图(或列表)的方法,求两次抽出的卡片上的图案恰好是短道速滑和花样滑冰的概率.
A.
 B.
B. C.
C. 17. 如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.
17. 如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.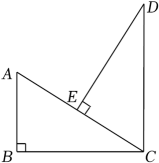 18. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何(马、牛单价各是多少两)?”19. 图①.图四、图③都是的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点叫做格点,故段的端点都在格点上.在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写画法.
18. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何(马、牛单价各是多少两)?”19. 图①.图四、图③都是的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点叫做格点,故段的端点都在格点上.在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写画法. (1)、在图①中画 , 使的面积是10;(2)、在图②中画四边形 , 使四边形是轴对称图形;(3)、在图③中的线段上找一点P , 使 .20. 如图,一次函数的图象与轴、轴分别相交于、两点,与反比例函数的图象相交于点 .
(1)、在图①中画 , 使的面积是10;(2)、在图②中画四边形 , 使四边形是轴对称图形;(3)、在图③中的线段上找一点P , 使 .20. 如图,一次函数的图象与轴、轴分别相交于、两点,与反比例函数的图象相交于点 . (1)、求反比例函数的表达式;(2)、点的横坐标为4,过点作轴平行线,交反比例函数的图象于点 , 连接 求的面积.21. 某快递公司为了解客户的使用体验,提升服务质量,随机抽取了500名用户进行问卷调查,并将调查问卷(部分)和结果描述如表:
(1)、求反比例函数的表达式;(2)、点的横坐标为4,过点作轴平行线,交反比例函数的图象于点 , 连接 求的面积.21. 某快递公司为了解客户的使用体验,提升服务质量,随机抽取了500名用户进行问卷调查,并将调查问卷(部分)和结果描述如表: (1)、如果将整体评价中的满意,一般,不满意分别赋分为5分,3分,1分,直接写出该公司此次调查中关于整体评价的中位数是 , 平均数是 .(2)、此次调查中,认为该公司最需要在包装细致方面进行改进的人数为多少?(3)、根据调查数据,请你为该公司下一步提升服务质量的工作提出两条合理的建议.22. 如图1是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,如图2,从侧面看,立柱DE高1.8米,踏板静止时踏板连杆与DE上的线段AB重合,BE长为0.2米,当踏板连杆绕着点A旋转到AC处时,测得∠CAB=37°,此时点C距离地面的高度CF为0.45米,求AB和AD的长(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)、如果将整体评价中的满意,一般,不满意分别赋分为5分,3分,1分,直接写出该公司此次调查中关于整体评价的中位数是 , 平均数是 .(2)、此次调查中,认为该公司最需要在包装细致方面进行改进的人数为多少?(3)、根据调查数据,请你为该公司下一步提升服务质量的工作提出两条合理的建议.22. 如图1是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,如图2,从侧面看,立柱DE高1.8米,踏板静止时踏板连杆与DE上的线段AB重合,BE长为0.2米,当踏板连杆绕着点A旋转到AC处时,测得∠CAB=37°,此时点C距离地面的高度CF为0.45米,求AB和AD的长(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 23. 某食品加工厂的甲、乙两个生产组领到了相同的加工任务,甲、乙两组以相同的工作效率同时开始工作,中途乙组因升级设备,停工了一段时间.乙组设备升级完毕后,提高了工作效率,在完成本组任务后,并帮助甲组加工了60 kg食品,最后两组同时停工,完成了此次加工任务,两组各自加工的食品量y(kg)与甲组工作时间x(h)之间的函数图象如图所示.
23. 某食品加工厂的甲、乙两个生产组领到了相同的加工任务,甲、乙两组以相同的工作效率同时开始工作,中途乙组因升级设备,停工了一段时间.乙组设备升级完毕后,提高了工作效率,在完成本组任务后,并帮助甲组加工了60 kg食品,最后两组同时停工,完成了此次加工任务,两组各自加工的食品量y(kg)与甲组工作时间x(h)之间的函数图象如图所示.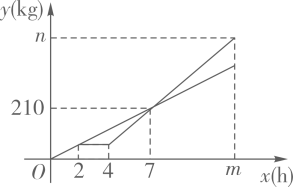 (1)、甲组每小时加工食品kg,乙组升级设备后每小时加工食品kg.(2)、求乙组设备升级完毕后y与x之间的函数关系式.(3)、求m、n的值.24. 如图1,在中, , , . 以为边,在外作等边 , D是的中点,连接并延长,交于点E .
(1)、甲组每小时加工食品kg,乙组升级设备后每小时加工食品kg.(2)、求乙组设备升级完毕后y与x之间的函数关系式.(3)、求m、n的值.24. 如图1,在中, , , . 以为边,在外作等边 , D是的中点,连接并延长,交于点E . (1)、直接写出边的长为;(2)、求证:四边形是平行四边形;(3)、将图1中的四边形折叠,折痕为 , F在上,G在上:
(1)、直接写出边的长为;(2)、求证:四边形是平行四边形;(3)、将图1中的四边形折叠,折痕为 , F在上,G在上:①如图2,若使点C与点A重合,求的长;
②若使点C与的一边中点重合,直接写出的长是 ▲ .
25. 如图, , , , . 点P从点A出发,以每秒2个单位长度的速度沿折线向终点B运动,当点P与点A不重合时,过点P作于点D , 将线段绕点P顺时针旋转得到线段 , 连接 . 设点P的运动时间为x秒,和重叠部分的图形面积为y . (1)、当点P与点C重合时,;(2)、当点E在上时,;(3)、求y关于x的函数解析式,并写出x的取值范围.26. 在平面直角坐标系中,二次函数的图象交x轴于点和点 .
(1)、当点P与点C重合时,;(2)、当点E在上时,;(3)、求y关于x的函数解析式,并写出x的取值范围.26. 在平面直角坐标系中,二次函数的图象交x轴于点和点 . (1)、此二次函数的图象与y轴的交点的纵坐标为 .(2)、求此二次函数的关系式.(3)、当时,求二次函数的最大值和最小值.(4)、点P为二次函数图象上任意一点,其横坐标为m,过点P作轴,点Q的横坐标为 . 已知点P与点Q不重合,且线段PQ的长度随m的增大而减小.直接写出线段PQ与二次函数的图象只有1个公共点时m的取值范围.
(1)、此二次函数的图象与y轴的交点的纵坐标为 .(2)、求此二次函数的关系式.(3)、当时,求二次函数的最大值和最小值.(4)、点P为二次函数图象上任意一点,其横坐标为m,过点P作轴,点Q的横坐标为 . 已知点P与点Q不重合,且线段PQ的长度随m的增大而减小.直接写出线段PQ与二次函数的图象只有1个公共点时m的取值范围.