安徽省滁州市全椒县2023年中考三模数学试卷

试卷更新日期：2023-06-16 类型：中考模拟

进入出卷网下载

一、单选题

1. -2023的倒数是（）

A、 2023 B、 $- \frac{1}{2023}$ C、-2023 D、 $\frac{1}{2023}$

查看试题解析
2. 2022年，我国全年外贸规模再创历史新高．货物进出口突破了40万亿元大关，达到42.07万亿元，增长7.7%．数据“42.07万亿”用科学记数法表示为（）．

A、 $42.07 \times 10^{12}$ B、 $4.207 \times 10^{13}$ C、 $4.207 \times 10^{12}$ D、 $0.4207 \times 10^{14}$

查看试题解析
3. 下列计算结果为 $- a^{3} b^{6}$ 的是（）．

A、 $- {(a b^{3})}^{2}$ B、 ${(- a b^{3})}^{3}$ C、 $- {(a b^{2})}^{3}$ D、 $- {(a b^{3})}^{3}$

查看试题解析
4. 一张水平放置的桌子上摆放着若干个碟子，其三视图如图所示，则这张桌子上共有碟子的个数为（）

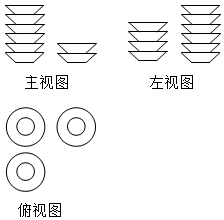A、10 B、12 C、14 D、18

查看试题解析
5. 已知一元二次方程 $a x^{2} - x + 2 = 0$ 有实根，a的取值范围是（）

A、 $a \leq \frac{1}{8}$ B、 $a \leq \frac{1}{8}$ 且 $a \neq 0$ C、 $a \leq - \frac{1}{8}$ D、 $a \leq \frac{1}{4}$ 且 $a \neq 0$

查看试题解析
6. 班长邀请 $A$ ， $B$ ， $C$ ， $D$ 四位同学参加圆桌会议.如图，班长坐在⑤号座位，四位同学随机坐在①②③④四个座位，则 $A$ ， $B$ 两位同学座位相邻的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

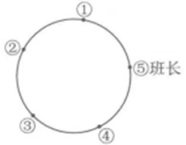查看试题解析
7. 如图是以O为圆心， $A B$ 为直径的圆形纸片，点C在 $⊙ O$ 上．将该纸片沿直线 $CO$ 对折，点B落在 $⊙ O$ 上的点D处（不与点A重合），连接 $C B$ ， $C D$ ， $A D$ ．设 $C D$ 与直径 $A B$ 交于点E ，若 $A D = E D$ ，则 $∠ B$ 的度数为（）．

A、 $24 °$ B、 $30 °$ C、 $36 °$ D、 $44 °$

查看试题解析
8. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ，通过尺规作图得到的直线 $M N$ 分别交 $A B$ ， $A C$ 于D ， E ．连接 $C D$ ，若 $C E = \frac{1}{3} A E = 1$ ，则 $C D$ 的长为（）．

A、2 B、3 C、 $\sqrt{5}$ D、 $\sqrt{6}$

查看试题解析
9. 已知一次函数 $y = 2 b x + (a + c)$ 的图象经过点 $(- 1 ， 0)$ ，且当 $x = 1$ 时， $y > 0$ ．则下列结论正确的是（）．

A、a ， c都为正，且 $b^{2} - a c \geq 0$ B、a ， c都为正，且 $b^{2} - a c > 0$ C、a ， c至少有一项为正，且 $b^{2} - a c \geq 0$ D、a ， c至少有一项为正，且 $b^{2} - a c > 0$

查看试题解析
10. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 2$ ， $B C = 1$ ，顶点A ， C分别在x轴、y轴的正半轴上滑动，则点B到原点O的最大距离是（）．

A、 $\sqrt{2}$ B、 $\sqrt{2} + 1$ C、 $\sqrt{3}$ D、 $\sqrt{2} + 2$

查看试题解析

二、填空题

11. 已知关于x的方程 $2 x - 3 k = 6 - x$ 的解为负数，则k的取值范围是．

查看试题解析
12. 因式分解： $a x^{2} - a y^{2} =$ ．

查看试题解析
13. 如图，在平面直角坐标系xOy中，点 $A$ （0，4）， $B$ （3，4），将 $△ A B O$ 向右平移到 $△ C D E$ 位置，A的对应点是 $C$ ， $O$ 的对应点是 $E$ ，函数 $y = \frac{k}{x} (k \neq 0)$ 的图像经过点 $C$ 和 $D E$ 的中点 $F$ ，则 $k$ 的值是．

查看试题解析
14. 四边形ABCD是边长为4的正方形，点E在边AD上，以EC为边作正方形CEFG（点D，点F在直线CE的同侧）.连接BF.

(1)、如图1，当点E与点A重合时， $BF=$ ；

(2)、如图2，当点E在线段AD上时， $AE= 1$ ，则 $BF=$ .

查看试题解析

三、解答题

15. 计算： ${(π - 2)}^{0} - \sqrt{8} + | 3 - \sqrt{2} | + 6 \sin 45 °$ ．

查看试题解析
16. 如图，由边长为1的小正方形组成的网格中建立平面直角坐标系 $x o y$ ， $△ A B C$ 的顶点均在网格线的交点上．

(1)、画出 $△ A B C$ 关于点B中心对称的 $△ D B E$ （点A、C的对应点分别是点D、E）

(2)、将 $△ A B C$ 平移，使点A平移到点 $(4 ， 0)$ 处．
①请画出平移后的 $△ A_{1} B_{1} C_{1}$ （点A、B、C的对应点分别是点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ ）

②若点 $P (a ， b)$ 为 $△ A B C$ 内一点，则平移后，点P的对应点的坐标为 ▲ （用含 $a$ 、 $b$ 的代数式表示）．

查看试题解析
17. 某社团在课余时间用无人机为学校航拍宣传片，如图所示的 $Δ A B C$ 为无人机某次空中飞行轨迹， $D$ 为 $B C$ 延长线上一点，点 $A$ ， $B$ ， $C$ ， $D$ 在同一平面内， $∠ B = 30 °$ ， $∠ A C D = 78.3 °$ ．若 $A C = 80$ 米，求 $A B$ 的长．（结果保留整数，参考数据： $\sin 78.3 ° \approx 0.98$ ， $\sin 48.3 ° \approx 0.75$ ， $\cos 48.3 ° \approx 0.67$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
18. 观察以下等式：
第1个等式： $\frac{1}{2} + \frac{1}{1 \times 2}$ =1，

第2个等式： $\frac{1}{3} + \frac{1}{2 \times 3} = \frac{1}{2}$ ，

第3个等式： $\frac{1}{4} + \frac{1}{3 \times 4} = \frac{1}{3}$ ，

第4个等式： $\frac{1}{5} + \frac{1}{4 \times 5} = \frac{1}{4}$ ，

第5个等式： $\frac{1}{6} + \frac{1}{5 \times 6} = \frac{1}{5}$ ，

……

按照以上规律，解决下列问题：

(1)、写出第6个等式：．

(2)、写出你猜想的第n个等式： ▲ (用含n的式子表示)，并证明其正确性．

查看试题解析
19. 某校为了丰富学生的课余生活，决定购买一定数量的乒乓球拍和羽毛球拍．某商店的乒乓球拍和羽毛球拍的销售方案如下表所示：

不足30副

30副及以上

乒乓球拍

按标价出售

每副优惠5元

羽毛球拍

按标价出售

按标价的8折出售

已知购买10副乒乓球拍和10副羽毛球拍需要1000元，购买15副乒乓球拍和5副羽毛球拍需要900元．若张老师购买40副乒乓球拍，50副羽毛球拍，则需花费多少元？

查看试题解析
20. 如图， $A B$ 是 $⊙ O$ 的直径，点C是 $⊙ O$ 上一点，连接 $A C ， B C$ ，点D在 $B A$ 的延长线上， $∠ D C A = ∠ A B C ， B E ⊥ D C$ ，交 $D C$ 的延长线于点E ．

(1)、求证： $D C$ 是 $⊙ O$ 的切线；

(2)、若 $\frac{O A}{O D} = \frac{1}{3}$ ， $B E = 4$ ，求 $△ B D E$ 的面积．

查看试题解析
21. 在大课间活动中，同学们积极参加体育锻炼，小明在全校随机抽取一部分同学就“一分钟跳绳”进行测试，并以测试数据为样本，分别绘制成如图1、图2所示的不完整的频数直方图（从左到右依次为第一小组到第六小组，每小组含最小值不含最大值）和扇形统计图．

根据图中提供的信息，完成下列问题：

(1)、本次抽样调查的总人数为；

(2)、将图1补充完整；

(3)、求第五小组对应圆心角的度数；

(4)、若“一分钟跳绳”次数不低于130次的成绩为优秀，全校共有1200名学生，根据图中提供的信息，估计该校“一分钟跳绳”成绩优秀的人数．

查看试题解析
22. “八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：①统计售价与需求量的数据，通过描点（图1），发现该蔬菜需求量 $y_{1}$ （吨）关于售价x（元/千克）的函数图象可以看成抛物线，其表达式为 $y_{1} = a x^{2} + c$ ，部分对应值如表：

售价x（元/千克）

…

2.5

3

3.5

4

…

需求量 $y_{1}$ （吨）

…

7.75

7.2

6.55

5.8

…

②该蔬菜供给量 $y_{2}$ （吨）关于售价x（元/千克）的函数表达式为 $y_{2} = x - 1$ ，函数图象见图1．

③1~7月份该蔬菜售价 $x_{1}$ （元/千克），成本 $x_{2}$ （元/千克）关于月份t的函数表达式分别为 $x_{1} = \frac{1}{2} t + 2$ ， $x_{2} = \frac{1}{4} t^{2} - \frac{3}{2} t + 3$ ，函数图象见图2．

请解答下列问题：

(1)、求a ， c的值．

(2)、根据图2，哪个月出售这种蔬菜每千克获利最大？并说明理由．

(3)、求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润．

查看试题解析
23. 在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $A D$ 平分 $∠ C A B$ 交 $B C$ 于点 $D$ ， $B E$ 平分 $∠ A B C$ 交 $A C$ 于点 $E$ ， $A D$ ， $B E$ 相交于点 $F$ ．

(1)、当 $A C = B C$ 时，如图1，求证： $△ A E F$ ≌ $△ B D F$ ；

(2)、连接 $C F$ ，如图2．
①求证： $△ A E F ∽ △ AFC$ ；

②若 $E F = 2 \sqrt{2}$ ， $A F = 8$ ，求 $A C$ 的长．

查看试题解析

	不足30副	30副及以上
乒乓球拍	按标价出售	每副优惠5元
羽毛球拍	按标价出售	按标价的8折出售

售价x（元/千克）	…	2.5	3	3.5	4	…
需求量 $y_{1}$ （吨）	…	7.75	7.2	6.55	5.8	…