安徽省合肥市蜀山区2023年中考三模数学试卷

试卷更新日期：2023-06-16 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣6的绝对值是（）

A、 $- 6$ B、 $6$ C、 $\pm 6$ D、 $- \frac{1}{6}$

查看试题解析
2. 中国人民解放军海军福建舰是中国的第三艘航空母舰，也是中国完全自主设计建造的首艘弹射型航空母舰．采用平直通长飞行甲板，配置电磁弹射和阻拦装置，满载排水量 $80000$ 余吨，数据 $80000$ 用科学记数法表示为（）

A、 $8 \times 10^{5}$ B、 $8 \times 10^{4}$ C、 $0.8 \times 10^{5}$ D、 $0.8 \times 10^{4}$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{2} \cdot a^{4} = a^{8}$ B、 ${(a - b)}^{2} = a^{2} - b^{2}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(- 2 a^{2} b)}^{2} = 4 a^{4} b^{2}$

查看试题解析
4. 如图所示的几何体是由一个长方体和一个圆柱组成的，则它的主视图是（）

A、 B、 C、 D、

查看试题解析
5. 将一直角三角形和矩形如图放置，若 $∠ 1 = 42 °$ ，则 $∠ 2 =$ （）

A、 $58 °$ B、 $54 °$ C、 $48 °$ D、 $44 °$

查看试题解析
6. 若关于x的一元二次方程 $m x^{2} + 4 x = x^{2} + 2$ 有实数根，则m的值有可能是（）

A、 $- 3$ B、 $- 2$ C、1 D、 $- 1$

查看试题解析
7. 如图，菱形 $A B C D$ 中，点E ， F ， G分别为 $A B ， B C ， C D$ 的中点， $E F = 2$ ， $F G = 4$ ，则菱形 $A B C D$ 的面积为（）

A、12 B、16 C、20 D、32

查看试题解析
8. 二进制是计算技术中广泛采用的一种数制，由18世纪德国数理哲学大师菜布尼兹发现，二进制数据是用0和1两个数码来表示的数，如01，10分别表示不同的二进制数，在有一个0，两个1组成的二进制数中，两个1相邻的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{5}{6}$

查看试题解析
9. 在边长为8的正方形 $A B C D$ 中，E为 $A B$ 边上一点， $A E = 3 B E$ ，连接 $D E$ ， G为 $D E$ 中点，若点M在正方形 $A B C D$ 的边上，且 $M G = 5$ ，则满足条件的点M的个数是（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
10. 已知，二次函数 $y = a x^{2} + (2 a - 1) x + 1$ 的对称轴为y轴，将此函数向下平移3个单位，若点M为二次函数图象在（ $- 1 \leq x \leq 1$ ）部分上任意一点，O为坐标原点，连接 $O M$ ，则 $O M$ 长度的最小值是（）

A、 $\sqrt{3}$ B、2 C、 $\frac{\sqrt{13}}{2}$ D、 $\frac{\sqrt{17}}{2}$

查看试题解析

二、填空题

11. -64的立方根是。

查看试题解析
12. 用半径为9，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面半径等于．

查看试题解析
13. 如图，在平面直角坐标系中，反比例函数 $y = \frac{m}{x}$ （ $x > 0$ ， m为常数）的图象与一次函数 $y = k x + b$ 的图象交于点 $A (2 ， a)$ 和点B ，过点A、B分别作x、y轴的垂线，交x轴于点C ，交y轴于点D ， $A C$ 与 $B D$ 交于点E ，若点E恰为 $A C$ 中点，三角形 $A D C$ 的面积为4，则k的值为．

查看试题解析
14. 如图，△ABC中， $∠ A B C = 90 °$ ， $A B = B C$ ，点D是边AC上一点， $C D = 2 A D$ ，连接BD ，过点C作 $C E ⊥ B D$ 于点E ，连接AE ．

(1)、 $∠ A E C =$ °；

(2)、若 $B C = 3 \sqrt{5}$ ，则 $A E =$ ．

查看试题解析

三、解答题

15. 解不等式组： ${\begin{array}{l} 2 x - 1 \geq 5 ① \\ \frac{2 x + 1}{3} > x - 1 ② \end{array}$ ．

查看试题解析
16. 化简： $\frac{a^{2} - 2 a + 1}{a^{2} + a} \div (1 - \frac{2}{a + 1})$ ．

查看试题解析
17. 意大利著名数学家斐波那契在研究兔子繁殖问题时，发现这样一组数：1，1，2，3，5，8，13，…，现以这组数中的各个数作为正方形的边长，依次构造一组正方形，再分别从左到右取2个，3个，4个，5个正方形拼成如下的长方形．并记为长方形①，长方形②，长方形③，长方形④．

(1)、规律探究：如图1所示，第8个正方形的边长为

(2)、如图2所示，相应长方形的周长如表所示，

序号

①

②

③

④

⑤

周长

6

10

16

x

y

若按此规律继续作长方形，则 $x =$ ， $y =$ ；

(3)、拓展延伸：按一定规律排列的一列数： $10^{1}$ ， $10^{2}$ ， $10^{3}$ ， $10^{5}$ ， $10^{8}$ ， $10^{13}$ ， …，若x、y、z表示这列数中的连续三个数且 $x < y < z$ ，猜想x、y、z满足的关系式是．

查看试题解析
18. 如图，在每个小正方形的边长为1个单位的网格中， $△ A B C$ 的顶点均在格点（网格线的交点）上．

(1)、画出将 $△ A B C$ 向右平移3个单位，再向上平移5个单位后的 $△ A_{1} B_{1} C_{1}$ （点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 分别为A ， B ， C的对应点）；

(2)、将（1）中的 $△ A_{1} B_{1} C_{1}$ 绕点O顺时针旋转90°得到 $△ A_{2} B_{2} C_{2}$ （点 $A_{2}$ ， $B_{2}$ ， $C_{2}$ 分别为 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的对应点）；

(3)、仅用无刻度的直尺作 $∠ A B C$ 的平分线交 $A C$ 于点D ．

查看试题解析
19. 如图，某地需要经过一座山的两侧D ， E修建一条穿山隧道，工程人员先选取直线 $D E$ 上的三点A ， B ， C ，设在隧道 $D E$ 正上方的山顶F处测得A处的俯角为 $15 °$ ， B处的俯角为 $30 °$ ， C处的俯角为 $45 °$ ，经测量 $A B = 1.4$ 千米， $B D = 0.2$ 千米， $C E = 0.5$ 千米，求隧道 $D E$ 的长．（结果精确到 $0.1$ ， $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
20. 如图， $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点E ，过点D作 $⊙ O$ 的切线交 $A B$ 的延长线于点F ．

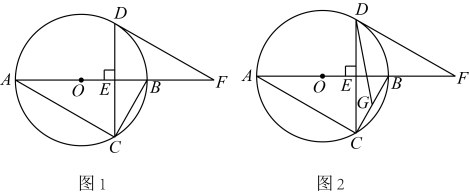(1)、如图1，若 $∠ A = α$ ，求 $∠ F D E$ （用含 $α$ 代数式表示）：

(2)、如图2，取 $B C$ 的中点G ，连接 $D G$ ，若 $∠ A = 30 °$ ， $D G = \sqrt{7}$ ，求 $⊙ O$ 的半径．

查看试题解析

21. 某校开展“书香校园”课外读书周活动，活动结束后，经初步统计，所有学生的课外阅读时长都不低于6小时，但不足12小时，从七，八年级中各随机抽取了20名学生，对他们在活动期间课外阅读时长x（单位：小时）进行整理、描述和分析（

6 \leq x < 7

，记为6小时；

7 \leq x < 8

，记为7小时：

8 \leq x < 9

，记为8小时…以此类推），下面分别给出了抽取的学生课外阅读时长的部分信息．

七，八年级抽取的学生课外阅读时长统计表
年级	七年级	八年级
平均数	8.3	a
中位数	8	b
众数	c	9
方差	1.48	2.01

根据以上信息回答下列问题：

(1)、计算a的值：

(2)、填空：

b =

；

c =

；

(3)、根据以上数据，你认为该校七，八年级学生在课外读书周活动中，哪个年级学生的阅读积极性更高？（请写出两条理由）

查看试题解析

22. 如图，在四边形 $A B C D$ 中， $∠ A B C = 120 °$ ，对角线 $B D$ 平分 $∠ A B C$ ， $B D = B C$ ， E为 $B D$ 上一点，且 $B A = B E$ ，连接 $A C$ 交 $B D$ 于点F ， G为 $B C$ 上一点，满足 $B F = B G$ ，连接 $E G$ 交 $A C$ 于点H ，连接 $B H$ ．

(1)、①求证： $∠ E H F = 60 °$ ；
②若H为 $E G$ 中点，求证： $A F^{2} = 2 E F \cdot E B$ ；

(2)、若 $A C$ 平分 $∠ D A B$ ，请直接写出 $∠ E C A$ 与 $∠ A C B$ 的关系：．

查看试题解析
23. 如图，在平面直角坐标系 $x O y$ 中，抛物线 $y = - x^{2} + b x + c$ 与x轴相交于不同的两点A、B ，且该抛物线的顶点E在矩形 $A B C D$ 的边 $C D$ 上， $A D = 4$ ．

(1)、若点A坐标为 $(1 ， 0)$ ．
①求该抛物线的关系式：

②若点 $P (m ， y_{1})$ ， $Q (n ， y_{2})$ 都在此抛物线上，且 $- 2 \leq m < - 1$ ， $0 < n < \frac{1}{2}$ ．试比较 $y_{1}$ 与 $y_{2}$ 大小，并说明理由；

(2)、求边 $A B$ 的长度．

查看试题解析

序号	①	②	③	④	⑤
周长	6	10	16	x	y