安徽省合肥市庐江县2023年中考三模数学试卷
试卷更新日期:2023-06-16 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 电信诈骗是指通过电话、网络和短信方式,编造虚假信息,设置骗局,对受害人实施远程、非接触式诈骗,诱使受害人打款或转账的犯罪行为.相关资料显示,2022年全国电信诈骗金额总数达到2万亿人民币.这里的数字“2万亿”用科学记数法表示为( )A、 B、 C、 D、3. 如图所示的某种零件的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 下图是甲乙丙三位同学在一次长跑练习中所用时间与路程之间的函数图象,其中最先到达终点和平均速度最快的分别是( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 下图是甲乙丙三位同学在一次长跑练习中所用时间与路程之间的函数图象,其中最先到达终点和平均速度最快的分别是( ) A、甲和乙 B、甲和丙 C、丙和甲 D、丙和乙6. 如图,中, , , 垂足为 , 平分交于 , 点是关于的对称点,连接 . 若 , 则的度数是( )
A、甲和乙 B、甲和丙 C、丙和甲 D、丙和乙6. 如图,中, , , 垂足为 , 平分交于 , 点是关于的对称点,连接 . 若 , 则的度数是( ) A、 B、 C、 D、7. 若关于的方程有实数根,则的取值不可以是( )A、0 B、1 C、2 D、38. 赵希的笔袋里装有5支同一品牌、同一型号的中性笔,其中有2支黑色,2支红色和1支蓝色,上课时,赵希随机的从笔袋中取出一只,若正好是黑色中性笔的概率是( )A、 B、 C、 D、9. 在同一平面直角坐标系内,二次函数与一次函数的图像可能是( )A、
A、 B、 C、 D、7. 若关于的方程有实数根,则的取值不可以是( )A、0 B、1 C、2 D、38. 赵希的笔袋里装有5支同一品牌、同一型号的中性笔,其中有2支黑色,2支红色和1支蓝色,上课时,赵希随机的从笔袋中取出一只,若正好是黑色中性笔的概率是( )A、 B、 C、 D、9. 在同一平面直角坐标系内,二次函数与一次函数的图像可能是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,是半圆的直径,是弦,点是的中点,点是的中点,连接、分别交于点和点 , 连接 , 则下列结论中错误的是( )
10. 如图,是半圆的直径,是弦,点是的中点,点是的中点,连接、分别交于点和点 , 连接 , 则下列结论中错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:.12. 因式分解:.13. 如图,四边形中, , 点、分别是、的中点,连接 , 若 , , 若 , 则.
 14. 已知,如图,反比例函数经过点.
14. 已知,如图,反比例函数经过点.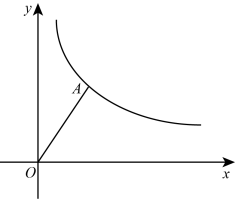 (1)、 ;(2)、平移至 , 使点的对应点落在坐标轴上,点的对应点落在反比例函数的图像上,若平行四边形的面积为12,则的值是 .
(1)、 ;(2)、平移至 , 使点的对应点落在坐标轴上,点的对应点落在反比例函数的图像上,若平行四边形的面积为12,则的值是 .三、解答题
-
15. 解不等式组: .16. 如图,在边长为1个单位长度的网格中,的顶点均在格点上,为经过网格线的一条直线.
 (1)、作出关于直线对称的;(2)、将向右平移个单位,再向下平移 ▲ 个单位,使两点的对应点落在直线的两侧,请画出图形.17. 受连日暴雨影响,某地甲乙两个村庄穴发泥石流灾害,急需从市中心东,西两个储备仓库调运救灾物资.已知这两个储备仓库均有救灾物资吨,其中村需要吨,村需要吨.从东仓库运往、两村的运费分别为元/吨和元/吨,从西仓库运往、两村的运费分别为元/吨和元/吨.(1)、设从东仓调运吨救灾物资去村,完成下列表格:
(1)、作出关于直线对称的;(2)、将向右平移个单位,再向下平移 ▲ 个单位,使两点的对应点落在直线的两侧,请画出图形.17. 受连日暴雨影响,某地甲乙两个村庄穴发泥石流灾害,急需从市中心东,西两个储备仓库调运救灾物资.已知这两个储备仓库均有救灾物资吨,其中村需要吨,村需要吨.从东仓库运往、两村的运费分别为元/吨和元/吨,从西仓库运往、两村的运费分别为元/吨和元/吨.(1)、设从东仓调运吨救灾物资去村,完成下列表格:运往村的物资/吨
运往村的物资/吨
东仓库
西仓库
(2)、调运结束之后,结算运费时发现,支付给东西两个仓库的运费相差元,求的值.18. 观察下面的图形及其对应的等式.图1:

图2:

图3:

图4:

……
按照上面图形与等式的对应规律,解决下面的问题:
(1)、写出图5对应的等式:.
(2)、写出图对应的等式(用含的等式表示),并证明.19. 下图是某游乐园的平面示意图,围墙、分别平行于两条互相垂直的街道.小敏利用所学知识,经过测量和换算发现: , , 出口到、两点的距离相等,到围墙的距离是 , 试求出口到围墙的距离及的长度.(结果精确到)参考数据: , , , , , .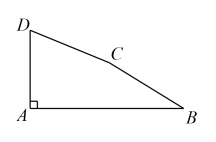 20. 已知,如图,四边形内接于 , 直线与相切,切点为 , 连接 .
20. 已知,如图,四边形内接于 , 直线与相切,切点为 , 连接 .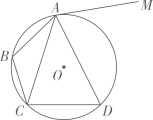 (1)、求证:;(2)、若 , 点是劣弧的中点, , 求 .21. 某校九年级学生正积极准备理化实验操作考试,为了解学生的准备情况,九年级(1)班的物理老师进行了一次模拟考试,让学生在A、B、C、D四个考题中任意抽取一个考题进行现场操作,除2人因操作失误得零分之外,其余同学的成绩均不低于7分.课代表对模拟成绩进行了记录汇总,并制成如下不完整的频数分布直方图和扇形统计图:
(1)、求证:;(2)、若 , 点是劣弧的中点, , 求 .21. 某校九年级学生正积极准备理化实验操作考试,为了解学生的准备情况,九年级(1)班的物理老师进行了一次模拟考试,让学生在A、B、C、D四个考题中任意抽取一个考题进行现场操作,除2人因操作失误得零分之外,其余同学的成绩均不低于7分.课代表对模拟成绩进行了记录汇总,并制成如下不完整的频数分布直方图和扇形统计图: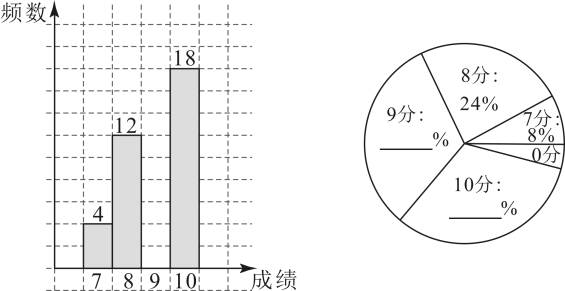 (1)、补全频数分布直方图和扇形统计图;(2)、求九年级(1)班本次模拟考试的平均分;(3)、根据往年的经验,学生再经过一定时间的强化训练,得分不低于8分的学生中约有的学生能够在理化实验操作考试中拿到满分,若该校九年级共有1000人,估计在今年的理化实验操作考试中能得满分的人数?
(1)、补全频数分布直方图和扇形统计图;(2)、求九年级(1)班本次模拟考试的平均分;(3)、根据往年的经验,学生再经过一定时间的强化训练,得分不低于8分的学生中约有的学生能够在理化实验操作考试中拿到满分,若该校九年级共有1000人,估计在今年的理化实验操作考试中能得满分的人数?

