安徽省蚌埠市2023年中考三模数学试卷
试卷更新日期:2023-06-16 类型:中考模拟
一、单选题
-
1. 在数轴上,点 , 关于原点对称.若点对应的数为5,则点对应的数是( )A、-5 B、10 C、0 D、52. 据安徽统计局公布,年月份,全省进出口总额亿元,用科学记数法表示亿,正确的是( )A、 B、 C、 D、3. 如图,该几何体的左视图是( )
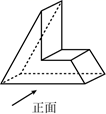 A、
A、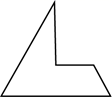 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 在数轴上表示不等式组的解集,正确的是( )A、
4. 下列运算正确的是( )A、 B、 C、 D、5. 在数轴上表示不等式组的解集,正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,电路图上有三个开关S1 , S2 , S3和两个小灯泡L1 , L2 , 随机闭合开关S1 , S2 , S3中的两个,能让灯泡L2发光的概率是( )
6. 如图,电路图上有三个开关S1 , S2 , S3和两个小灯泡L1 , L2 , 随机闭合开关S1 , S2 , S3中的两个,能让灯泡L2发光的概率是( ) A、 B、 C、 D、7. 如图推理中,空格①②③④处可以填上条件“对角线相等”的是( )
A、 B、 C、 D、7. 如图推理中,空格①②③④处可以填上条件“对角线相等”的是( ) A、①② B、①④ C、③④ D、②③8. 如图,蚌埠市教育局统计了2023年2月20日-3月31日局属八校实验室使用情况,通报给出了完全中学(含初高中)和高级中学(只有高中)实验室使用次数排行,仅根据这些信息,以下推断正确的是( )
A、①② B、①④ C、③④ D、②③8. 如图,蚌埠市教育局统计了2023年2月20日-3月31日局属八校实验室使用情况,通报给出了完全中学(含初高中)和高级中学(只有高中)实验室使用次数排行,仅根据这些信息,以下推断正确的是( )高级中学排名 1 蚌埠一中 2 蚌埠二中 3 蚌埠三中 4 蚌埠四中 完全中学排名 1 田家炳中学 2 蚌埠五中 3 铁路中学 4 蚌埠九中 A、蚌埠二中实验室使用总次数与田家炳中学实验室使用总次数相同 B、蚌埠二中平均每个年级使用次数高于蚌埠一中平均每个年级使用次数 C、蚌埠二中平均每个年级使用次数高于田家炳中学平均每个年级使用次数 D、蚌埠二中平均每个班级使用次数高于蚌埠九中平均每个年级使用次数9. 如图,已知: , , 求证: . 在证明该结论时,需添加辅助线,则以下关于秿助线的作法不正确的是( ) A、延长交的延长线于点 B、连接 C、分别作 , 的平分线 , D、过点作(点在点左侧),过点作(点在点左侧)10. 已知某拋物线开口向下,经过点 , , , 且 . 若点 , , 在该抛物线上,则( )A、 B、 C、 D、
A、延长交的延长线于点 B、连接 C、分别作 , 的平分线 , D、过点作(点在点左侧),过点作(点在点左侧)10. 已知某拋物线开口向下,经过点 , , , 且 . 若点 , , 在该抛物线上,则( )A、 B、 C、 D、二、填空题
-
11. 计算: .12. 如图,是内接四边形的一个外角,若 , 则的大小为 .
 13. 已知一组数 , , 3, , , , , , …,排列方式如下: , , 3,; , , , ;….若3的位置记为 , 的位置记为 , 则的位置记为 .14. 如图,点是线段上一动点, , 均为等边三角形, , 连接 .
13. 已知一组数 , , 3, , , , , , …,排列方式如下: , , 3,; , , , ;….若3的位置记为 , 的位置记为 , 则的位置记为 .14. 如图,点是线段上一动点, , 均为等边三角形, , 连接 . (1)、若 , 则;(2)、 长度的最小值为 .
(1)、若 , 则;(2)、 长度的最小值为 .三、解答题
-
15. 化简: , 并给出的值,使得该式的值为0.16. 在举办“智慧大阅读”的某一项比赛现场,组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共12个,若桌子腿数与凳子腿数的和为40条,则每个比赛场地有几张桌子和几条凳子?17. 如图,在由边长为个单位长度的小正方形组成的网格中,的顶点均为格点(网格线的交点),其中点 , , 的坐标分别为 , , .

⑴将平移,使得平移后对应点的坐标为 , 请画出;
18. 如图,是的直径,将弦绕点顺时针旋转得到 , 此时点的对应点落在上,延长 , 交于点 . (1)、证明:;(2)、若 , 求图中阴影部分的面积.19. 蚌埠位于安徽省东北部,淮河中游,地处秦岭淮河一线,大约在北纬位置.蚌埠市南北分界线雕塑(如图1)由中国当代艺术大师韩美林先生创作,名为《火凤凰·龙》.在某数学活动课上,老师带领学生前往该处测量雕塑的高度.如图2,在处用高米(即图中线段的长)的测角仪测得雕塑顶点的仰角为 , 向雕塑的方向前进米后到达处,在处测得雕塑顶点的仰角为 , 求整个雕塑的高(结果精确到米,参考数据: , . )
(1)、证明:;(2)、若 , 求图中阴影部分的面积.19. 蚌埠位于安徽省东北部,淮河中游,地处秦岭淮河一线,大约在北纬位置.蚌埠市南北分界线雕塑(如图1)由中国当代艺术大师韩美林先生创作,名为《火凤凰·龙》.在某数学活动课上,老师带领学生前往该处测量雕塑的高度.如图2,在处用高米(即图中线段的长)的测角仪测得雕塑顶点的仰角为 , 向雕塑的方向前进米后到达处,在处测得雕塑顶点的仰角为 , 求整个雕塑的高(结果精确到米,参考数据: , . ) 20. 某学校开展“家国情•诵经典”读书活动.为了解学生的参与程度,从全校学生中随机抽取200人进行问卷调查,获取了他们每人平均每天阅读时间的数据(m/分钟).将收集的数据分为A,B,C,D,E五个等级,绘制成如下统计图表(尚不完整):
20. 某学校开展“家国情•诵经典”读书活动.为了解学生的参与程度,从全校学生中随机抽取200人进行问卷调查,获取了他们每人平均每天阅读时间的数据(m/分钟).将收集的数据分为A,B,C,D,E五个等级,绘制成如下统计图表(尚不完整):平均每天阅读时间统计表
等级
人数(频数)
A(10≤m<20)
5
B(20≤m<30)
10
C(30≤m<40)
x
D(40≤m<50)
80
E(50≤m≤60)
y

请根据图表中的信息,解答下列问题:
(1)、求x的值;(2)、这组数据的中位数所在的等级是;(3)、学校拟将平均每天阅读时间不低于50分钟的学生评为“阅读达人”予以表扬.若全校学生以1800人计算,估计受表扬的学生人数.21. 如图,直线与反比例函数在第一条限内交于 , 两点,轴上的点满足 . (1)、若点坐标为 , 求点的坐标;(2)、若的面积为 , 求实数的值;(3)、设点 , 的坐标分别为 , , 求的值.22. 如图,为正方形的边上一点,为等腰直角三角形,其中 .
(1)、若点坐标为 , 求点的坐标;(2)、若的面积为 , 求实数的值;(3)、设点 , 的坐标分别为 , , 求的值.22. 如图,为正方形的边上一点,为等腰直角三角形,其中 . (1)、如图1,连接 , 求的大小;(2)、设交对角线于点 , 斜边交对角线于点 , 交边于点 .
(1)、如图1,连接 , 求的大小;(2)、设交对角线于点 , 斜边交对角线于点 , 交边于点 .①如图2,若 , 求的长;
②如图3,若为中点,求的值.
23. 如图,矩形是某生态农庄的一块植物栽培基地平面图,现欲修一条笔直的小路(宽度不计)经过该矩形区域,其中 , 都在矩形的边界上.已知 , (单位:百米),小路将矩形分成面积为 , (单位:平方百米)的两部分,其中 , 且点在面积为的区域内,记小路的长为百米. (1)、如图1,已知 , 设百米.
(1)、如图1,已知 , 设百米.①若 , 求的大小;
②求的最大值;
(2)、若 , 点在边上,点在边上,求的取值范围.