四川省达州市2023年中考数学试卷
试卷更新日期:2023-06-15 类型:中考真卷
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列图形中,是长方体表面展开图的是( )A、
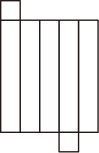 B、
B、 C、
C、 D、
D、 3. 某市政府在2022年着力稳定宏观经济大盘,全市经济发展取得新成效,全年生产总值实现2502.7亿元.数据2502.7亿用科学记数法表示为( )A、 B、 C、 D、4. 一组数据2,3,5,2,4,则这组数据的众数和中位数分别为( )A、3和5 B、2和5 C、2和3 D、3和25. 如图, , 平分 , 则( )
3. 某市政府在2022年着力稳定宏观经济大盘,全市经济发展取得新成效,全年生产总值实现2502.7亿元.数据2502.7亿用科学记数法表示为( )A、 B、 C、 D、4. 一组数据2,3,5,2,4,则这组数据的众数和中位数分别为( )A、3和5 B、2和5 C、2和3 D、3和25. 如图, , 平分 , 则( ) A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 某镇的“脆红李”深受广大市民的喜爱,也是馈赠亲友的尚佳礼品,首批“脆红李”成熟后,当地某电商用12000元购进这种“脆红李”进行销售,面市后,线上订单猛增供不应求,该电商又用11000元购进第二批这种“脆红李”,由于更多“脆红李”成熟,单价比第一批每件便宜了5元,但数量比第一批多购进了40件,求购进的第一批“脆红李”的单价.设购进的第一批“脆红李”的单价为x元/件,根据题意可列方程为( )A、 B、 C、 D、8. 下列命题中,是真命题的是( )A、平行四边形是轴对称图形 B、对角线互相垂直的四边形是菱形 C、到一条线段两个端点距离相等的点,在这条线段的垂直平分线上 D、在中,若 , 则是直角三角形9. 如图,四边形是边长为的正方形,曲线是由多段的圆心角的圆心为 , 半径为;的圆心为 , 半径为的圆心依次为循环,则的长是( )
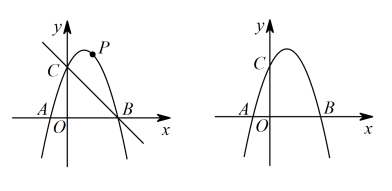
A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 某镇的“脆红李”深受广大市民的喜爱,也是馈赠亲友的尚佳礼品,首批“脆红李”成熟后,当地某电商用12000元购进这种“脆红李”进行销售,面市后,线上订单猛增供不应求,该电商又用11000元购进第二批这种“脆红李”,由于更多“脆红李”成熟,单价比第一批每件便宜了5元,但数量比第一批多购进了40件,求购进的第一批“脆红李”的单价.设购进的第一批“脆红李”的单价为x元/件,根据题意可列方程为( )A、 B、 C、 D、8. 下列命题中,是真命题的是( )A、平行四边形是轴对称图形 B、对角线互相垂直的四边形是菱形 C、到一条线段两个端点距离相等的点,在这条线段的垂直平分线上 D、在中,若 , 则是直角三角形9. 如图,四边形是边长为的正方形,曲线是由多段的圆心角的圆心为 , 半径为;的圆心为 , 半径为的圆心依次为循环,则的长是( ) A、 B、 C、 D、10. 如图,拋物线(为常数)关于直线对称.下列五个结论:①;②;③;④;⑤ . 其中正确的有( )
A、 B、 C、 D、10. 如图,拋物线(为常数)关于直线对称.下列五个结论:①;②;③;④;⑤ . 其中正确的有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 函数y= 的自变量x的取值范围是 .
12. 已知是方程的两个实数根,且 , 则的值为 .13. 如图,乐器上的一根弦 , 两个端点固定在乐器板面上,支撑点是靠近点的黄金分割点,支撑点是靠近点的黄金分割点,之间的距离为 .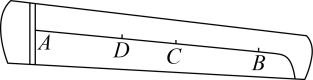 14. 如图,一次函数与反比例函数的图象相交于两点,以为边作等边三角形 , 若反比例函数的图象过点 , 则的值为 .
14. 如图,一次函数与反比例函数的图象相交于两点,以为边作等边三角形 , 若反比例函数的图象过点 , 则的值为 .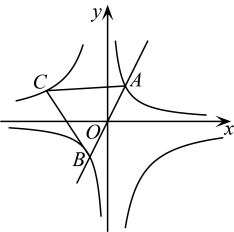 15. 在中, , , 在边上有一点 , 且 , 连接 , 则的最小值为 .
15. 在中, , , 在边上有一点 , 且 , 连接 , 则的最小值为 .三、解答题
-
16.(1)、计算:;(2)、先化简,再求值; , 其中为满足的整数.17. 在深化教育综合改革、提升区域教育整体水平的进程中,某中学以兴趣小组为载体,加强社团建设,艺术活动学生参与面达 , 通过调查统计,八年级二班参加学校社团的情况(每位同学只能参加其中一项):A.剪纸社团,B.泥塑社团,C.陶笛社团,D.书法社团,E.合唱社团,并绘制了如下两幅不完整的统计图.
 (1)、该班共有学生 ▲ 人,并把条形统计图补充完整;(2)、扇形统计图中, , , 参加剪纸社团对应的扇形圆心角为度;(3)、小鹏和小兵参加了书法社团,由于参加书法社团几位同学都非常优秀,老师将从书法社团的学生中选取2人参加学校组织的书法大赛,请用“列表法”或“画树状图法”,求出恰好是小鹏和小兵参加比赛的概率.18. 如图,网格中每个小正方形的边长均为1,的顶点均在小正方形的格点上.
(1)、该班共有学生 ▲ 人,并把条形统计图补充完整;(2)、扇形统计图中, , , 参加剪纸社团对应的扇形圆心角为度;(3)、小鹏和小兵参加了书法社团,由于参加书法社团几位同学都非常优秀,老师将从书法社团的学生中选取2人参加学校组织的书法大赛,请用“列表法”或“画树状图法”,求出恰好是小鹏和小兵参加比赛的概率.18. 如图,网格中每个小正方形的边长均为1,的顶点均在小正方形的格点上. (1)、将向下平移3个单位长度得到 , 画出;(2)、将绕点顺时针旋转90度得到 , 画出;(3)、在(2)的运动过程中请计算出扫过的面积.19. 莲花湖湿地公园是当地人民喜爱的休闲景区之一,里面的秋千深受孩子们喜爱.如图所示,秋千链子的长度为 , 当摆角恰为时,座板离地面的高度为 , 当摆动至最高位置时,摆角为 , 求座板距地面的最大高度为多少?(结果精确到;参考数据: , , , , , )
(1)、将向下平移3个单位长度得到 , 画出;(2)、将绕点顺时针旋转90度得到 , 画出;(3)、在(2)的运动过程中请计算出扫过的面积.19. 莲花湖湿地公园是当地人民喜爱的休闲景区之一,里面的秋千深受孩子们喜爱.如图所示,秋千链子的长度为 , 当摆角恰为时,座板离地面的高度为 , 当摆动至最高位置时,摆角为 , 求座板距地面的最大高度为多少?(结果精确到;参考数据: , , , , , ) 20. 如图,在中, .
20. 如图,在中, . (1)、尺规作图:作的角平分线交于点(不写做法,保留作图痕迹);(2)、在(1)所作图形中,求的面积.21. 如图,内接于是延长线上的一点, , 相交于点 .
(1)、尺规作图:作的角平分线交于点(不写做法,保留作图痕迹);(2)、在(1)所作图形中,求的面积.21. 如图,内接于是延长线上的一点, , 相交于点 .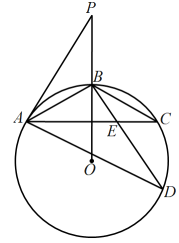 (1)、求证:是的切线;(2)、若 , , 求的长.22. 某县著名传统土特产品“豆笋”、“豆干”以“浓郁豆香,绿色健康”享誉全国,深受广大消费者喜爱.已知2件豆笋和3件豆干进货价为240元,3件豆笋和4件豆干进货价为340元.(1)、分别求出每件豆笋、豆干的进价;(2)、某特产店计划用不超过元购进豆笋、豆干共件,且豆笋的数量不低于豆干数量的 , 该特产店有哪几种进货方案?(3)、若该特产店每件豆笋售价为80元,每件豆干售价为55元,在(2)的条件下,怎样进货可使该特产店获得利润最大,最大利润为多少元?23. 【背景】在一次物理实验中,小冉同学用一固定电压为的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡(灯丝的阻值)亮度的实验(如图),已知串联电路中,电流与电阻之间关系为 , 通过实验得出如下数据:
(1)、求证:是的切线;(2)、若 , , 求的长.22. 某县著名传统土特产品“豆笋”、“豆干”以“浓郁豆香,绿色健康”享誉全国,深受广大消费者喜爱.已知2件豆笋和3件豆干进货价为240元,3件豆笋和4件豆干进货价为340元.(1)、分别求出每件豆笋、豆干的进价;(2)、某特产店计划用不超过元购进豆笋、豆干共件,且豆笋的数量不低于豆干数量的 , 该特产店有哪几种进货方案?(3)、若该特产店每件豆笋售价为80元,每件豆干售价为55元,在(2)的条件下,怎样进货可使该特产店获得利润最大,最大利润为多少元?23. 【背景】在一次物理实验中,小冉同学用一固定电压为的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡(灯丝的阻值)亮度的实验(如图),已知串联电路中,电流与电阻之间关系为 , 通过实验得出如下数据:…
1
3
4
6
…
…
4
3
2.4
2
…
 (1)、 , ;(2)、【探究】根据以上实验,构建出函数 , 结合表格信息,探究函数的图象与性质.
(1)、 , ;(2)、【探究】根据以上实验,构建出函数 , 结合表格信息,探究函数的图象与性质.①在平面直角坐标系中画出对应函数的图象;

②随着自变量的不断增大,函数值的变化趋势是 ▲ .
(3)、【拓展】结合(2)中函数图象分析,当时,的解集为 .