四川省自贡市2023年中考数学试卷
试卷更新日期:2023-06-15 类型:中考真卷
一、单选题
-
1. 如图,数轴上点A表示的数是2023, , 则点B表示的数是( )
 A、2023 B、 C、 D、2. 自贡恐龙博物馆今年“五一”期间接待游客约人.人数用科学记数法表示为( )A、 B、 C、 D、3. 如图中六棱柱的左视图是( )
A、2023 B、 C、 D、2. 自贡恐龙博物馆今年“五一”期间接待游客约人.人数用科学记数法表示为( )A、 B、 C、 D、3. 如图中六棱柱的左视图是( ) A、
A、 B、
B、 C、
C、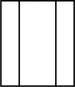 D、
D、 4. 如图,某人沿路线行走,与方向相同, , 则( )
4. 如图,某人沿路线行走,与方向相同, , 则( )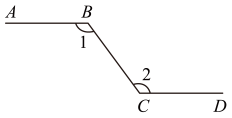 A、 B、 C、 D、5. 如图,边长为的正方形两边与坐标轴正半轴重合,点的坐标是( )
A、 B、 C、 D、5. 如图,边长为的正方形两边与坐标轴正半轴重合,点的坐标是( ) A、 B、 C、 D、6. 下列交通标志图案中,既是中心对称图形又是轴对称图形的是( )A、
A、 B、 C、 D、6. 下列交通标志图案中,既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 下列说法正确的是( )A、甲、乙两人10次测试成绩的方差分别是 , 则乙的成绩更稳定 B、某奖券的中奖率为 , 买100张奖券,一定会中奖1次 C、要了解神舟飞船零件质量情况,适合采用抽样调查 D、是不等式的解,这是一个必然事件8. 如图,内接于 , 是的直径,连接 , , 则的度数是( )
7. 下列说法正确的是( )A、甲、乙两人10次测试成绩的方差分别是 , 则乙的成绩更稳定 B、某奖券的中奖率为 , 买100张奖券,一定会中奖1次 C、要了解神舟飞船零件质量情况,适合采用抽样调查 D、是不等式的解,这是一个必然事件8. 如图,内接于 , 是的直径,连接 , , 则的度数是( )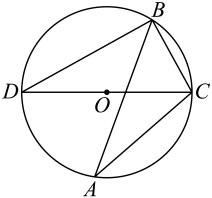 A、 B、 C、 D、9. 第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角 , 算出这个正多边形的边数是( )
A、 B、 C、 D、9. 第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角 , 算出这个正多边形的边数是( )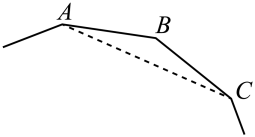 A、9 B、10 C、11 D、1210. 如图1,小亮家、报亭、羽毛球馆在一条直线上.小亮从家跑步到羽毛球馆打羽毛球,再去报亭看报,最后散步回家.小亮离家距离y与时间x之间的关系如图2所示.下列结论错误的是( )
A、9 B、10 C、11 D、1210. 如图1,小亮家、报亭、羽毛球馆在一条直线上.小亮从家跑步到羽毛球馆打羽毛球,再去报亭看报,最后散步回家.小亮离家距离y与时间x之间的关系如图2所示.下列结论错误的是( ) A、小亮从家到羽毛球馆用了分钟 B、小亮从羽毛球馆到报亭平均每分钟走米 C、报亭到小亮家的距离是米 D、小亮打羽毛球的时间是分钟11. 经过两点的抛物线(为自变量)与轴有交点,则线段长为( )A、10 B、12 C、13 D、1512. 如图,分别经过原点和点的动直线 , 夹角 , 点是中点,连接 , 则的最大值是( )
A、小亮从家到羽毛球馆用了分钟 B、小亮从羽毛球馆到报亭平均每分钟走米 C、报亭到小亮家的距离是米 D、小亮打羽毛球的时间是分钟11. 经过两点的抛物线(为自变量)与轴有交点,则线段长为( )A、10 B、12 C、13 D、1512. 如图,分别经过原点和点的动直线 , 夹角 , 点是中点,连接 , 则的最大值是( )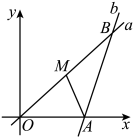 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 计算: .14. 请写出一个比小的整数 .15. 化简 .16. 端午节早上,小颖为全家人蒸了2个蛋黄粽,3个鲜肉粽,她从中随机挑选了两个孝敬爷爷奶奶,请问爷爷奶奶吃到同类粽子的概率是 .17. 如图,小珍同学用半径为 , 圆心角为的扇形纸片,制作一个底面半径为的圆锥侧面,则圆锥上粘贴部分的面积是 .
 18. 如图,直线与x轴,y轴分别交于A,B两点,点D是线段AB上一动点,点H是直线上的一动点,动点 , 连接 . 当取最小值时,的最小值是 .
18. 如图,直线与x轴,y轴分别交于A,B两点,点D是线段AB上一动点,点H是直线上的一动点,动点 , 连接 . 当取最小值时,的最小值是 .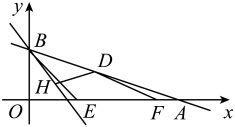
三、解答题
-
19. 计算: .20. 如图,在平行四边形中,点、分别在边和上,且 . 求证: .
 21. 某校组织七年级学生到江姐故里研学旅行,租用同型号客车4辆,还剩30人没有座位;租用5辆,还空10个座位.求该客车的载客量.22. 某校为了解“世界读书日”主题活动开展情况,对本学期开学以来学生课外读书情况进行了随机抽样调查,所抽取的12名学生课外读书数量(单位:本)数据如下:2,4,5,4,3,5,3,4,1,3,2,4.
21. 某校组织七年级学生到江姐故里研学旅行,租用同型号客车4辆,还剩30人没有座位;租用5辆,还空10个座位.求该客车的载客量.22. 某校为了解“世界读书日”主题活动开展情况,对本学期开学以来学生课外读书情况进行了随机抽样调查,所抽取的12名学生课外读书数量(单位:本)数据如下:2,4,5,4,3,5,3,4,1,3,2,4. (1)、补全学生课外读书数量条形统计图;(2)、请直接写出本次所抽取学生课外读书数量的众数、中位数和平均数;(3)、该校有600名学生,请根据抽样调查的结果,估计本学期开学以来课外读书数量不少于3本的学生人数.23. 如图1,一大一小两个等腰直角三角形叠放在一起, , 分别是斜边 , 的中点, .
(1)、补全学生课外读书数量条形统计图;(2)、请直接写出本次所抽取学生课外读书数量的众数、中位数和平均数;(3)、该校有600名学生,请根据抽样调查的结果,估计本学期开学以来课外读书数量不少于3本的学生人数.23. 如图1,一大一小两个等腰直角三角形叠放在一起, , 分别是斜边 , 的中点, . (1)、将绕顶点旋转一周,请直接写出点 , 距离的最大值和最小值;(2)、将绕顶点逆时针旋转(如图),求的长.24. 如图,点在反比例函数图象上.一次函数的图象经过点A,分别交x轴,y轴于点B,C,且与的面积比为 .
(1)、将绕顶点旋转一周,请直接写出点 , 距离的最大值和最小值;(2)、将绕顶点逆时针旋转(如图),求的长.24. 如图,点在反比例函数图象上.一次函数的图象经过点A,分别交x轴,y轴于点B,C,且与的面积比为 . (1)、求反比例函数和一次函数的解析式;(2)、请直接写出时,x的取值范围.25. 为测量学校后山高度,数学兴趣小组活动过程如下:
(1)、求反比例函数和一次函数的解析式;(2)、请直接写出时,x的取值范围.25. 为测量学校后山高度,数学兴趣小组活动过程如下: (1)、测量坡角
(1)、测量坡角如图1,后山一侧有三段相对平直的山坡 , 山的高度即为三段坡面的铅直高度之和,坡面的长度可以直接测量得到,要求山坡高度还需要知道坡角大小.
如图2,同学们将两根直杆的一端放在坡面起始端A处,直杆沿坡面方向放置,在直杆另一端N用细线系小重物G,当直杆与铅垂线重合时,测得两杆夹角的度数,由此可得山坡AB坡角的度数.请直接写出之间的数量关系.
(2)、测量山高同学们测得山坡的坡长依次为40米,50米,40米,坡角依次为;为求 , 小熠同学在作业本上画了一个含角的(如图3),量得 . 求山高 . ( , 结果精确到1米)
(3)、测量改进由于测量工作量较大,同学们围绕如何优化测量进行了深入探究,有了以下新的测量方法.

如图4,5,在学校操场上,将直杆NP置于的顶端,当与铅垂线重合时,转动直杆 , 使点N,P,D共线,测得的度数,从而得到山顶仰角 , 向后山方向前进40米,采用相同方式,测得山顶仰角;画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米,再画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米.已知杆高MN为米,求山高 . (结果用不含的字母表示)
26. 如图,抛物线与x轴交于 , 两点,与轴交于点 . (1)、求抛物线解析式及 , 两点坐标;(2)、以 , , , 为顶点的四边形是平行四边形,求点坐标;(3)、该抛物线对称轴上是否存在点 , 使得 , 若存在,求出点的坐标;若不存在,请说明理由.
(1)、求抛物线解析式及 , 两点坐标;(2)、以 , , , 为顶点的四边形是平行四边形,求点坐标;(3)、该抛物线对称轴上是否存在点 , 使得 , 若存在,求出点的坐标;若不存在,请说明理由.