四川省泸州市2023年中考数学试卷
试卷更新日期:2023-06-15 类型:中考真卷
一、单选题
-
1. 下列各数中,最大的是( )A、 B、0 C、2 D、2. 泸州市2022年全市地区生产总值()为2601.5亿元,将数据260150000000用科学记数法表示为( )A、 B、 C、 D、3. 如图, , 若 , 则的度数为( )
 A、 B、 C、 D、4. 一个立体图形的三视图如图所示,则该立体图形是( )
A、 B、 C、 D、4. 一个立体图形的三视图如图所示,则该立体图形是( )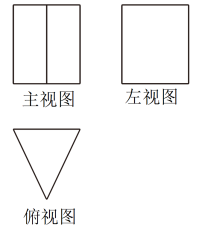 A、圆柱 B、圆锥 C、长方体 D、三棱柱5. 下列运算正确的是( )A、 B、 C、 D、6. 从1,2,3,4,5,5六个数中随机选取一个数,这个数恰为该组数据的众数的概率为( )A、 B、 C、 D、7. 如图,的对角线 , 相交于点 , 的平分线与边相交于点 , 是中点,若 , , 则的长为( )
A、圆柱 B、圆锥 C、长方体 D、三棱柱5. 下列运算正确的是( )A、 B、 C、 D、6. 从1,2,3,4,5,5六个数中随机选取一个数,这个数恰为该组数据的众数的概率为( )A、 B、 C、 D、7. 如图,的对角线 , 相交于点 , 的平分线与边相交于点 , 是中点,若 , , 则的长为( ) A、1 B、2 C、3 D、48. 关于的一元二次方程的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、实数根的个数与实数的取值有关9. 《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数 , , 的计算公式: , , , 其中 , , 是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是( )A、3,4,5 B、5,12,13 C、6,8,10 D、7,24,2510. 若一个菱形的两条对角线长分别是关于的一元二次方程的两个实数根,且其面积为11,则该菱形的边长为( )A、 B、 C、 D、11. 如图,在中, , 点在斜边上,以为直径的半圆与相切于点 , 与相交于点 , 连接 . 若 , , 则的长是( )
A、1 B、2 C、3 D、48. 关于的一元二次方程的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、实数根的个数与实数的取值有关9. 《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数 , , 的计算公式: , , , 其中 , , 是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是( )A、3,4,5 B、5,12,13 C、6,8,10 D、7,24,2510. 若一个菱形的两条对角线长分别是关于的一元二次方程的两个实数根,且其面积为11,则该菱形的边长为( )A、 B、 C、 D、11. 如图,在中, , 点在斜边上,以为直径的半圆与相切于点 , 与相交于点 , 连接 . 若 , , 则的长是( )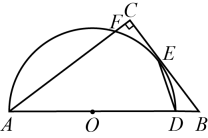 A、 B、 C、 D、12. 已知二次函数(其中是自变量),当时对应的函数值均为正数,则的取值范围为( )A、 B、或 C、或 D、或
A、 B、 C、 D、12. 已知二次函数(其中是自变量),当时对应的函数值均为正数,则的取值范围为( )A、 B、或 C、或 D、或二、填空题
-
13. 8的立方根为.14. 在平面直角坐标系中,若点与点关于原点对称,则的值是 .15. 关于 , 的二元一次方程组的解满足 , 写出的一个整数值 .16. 如图, , 是正方形的边的三等分点,是对角线上的动点,当取得最小值时,的值是 .

三、解答题
-
17. 计算: .18. 如图,点在线段上, , , . 求证: .
 19. 化简: .20. 某校组织全校800名学生开展安全教育,为了解该校学生对安全知识的掌握程度,现随机抽取40名学生进行安全知识测试,并将测试成绩(百分制)作为样本数据进行整理、描述和分析,下面给出了部分信息.
19. 化简: .20. 某校组织全校800名学生开展安全教育,为了解该校学生对安全知识的掌握程度,现随机抽取40名学生进行安全知识测试,并将测试成绩(百分制)作为样本数据进行整理、描述和分析,下面给出了部分信息.①将样本数据分成5组: , , , , , 并制作了如图所示的不完整的频数分布直方图;
②在这一组的成绩分别是:80,81,83,83,84,85,86,86,86,87,88,89.

根据以上信息,解答下列问题:
(1)、补全频数分布直方图;(2)、抽取的40名学生成绩的中位数是;(3)、如果测试成绩达到80分及以上为优秀,试估计该校800名学生中对安全知识掌握程度为优秀的学生约有多少人?21. 端午节是中国传统节日,人们有吃粽子的习俗.今年端午节来临之际,某商场预测A粽子能够畅销.根据预测,每千克A粽子节前的进价比节后多2元,节前用240元购进A粽子的数量比节后用相同金额购进的数量少4千克.根据以上信息,解答下列问题:(1)、该商场节后每千克A粽子的进价是多少元?(2)、如果该商场在节前和节后共购进A粽子400千克,且总费用不超过4600元,并按照节前每千克20元,节后每千克16元全部售出,那么该商场节前购进多少千克A粽子获得利润最大?最大利润是多少?22. 如图,某数学兴趣小组为了测量古树的高度,采用了如下的方法:先从与古树底端在同一水平线上的点A出发,沿斜面坡度为的斜坡前进到达点 , 再沿水平方向继续前进一段距离后到达点 . 在点处测得古树的顶端的俯角为 , 底部的俯角为 , 求古树的高度(参考数据: , , , 计算结果用根号表示,不取近似值). 23. 如图,在平面直角坐标系中,直线与 , 轴分别相交于点A,B,与反比例函数的图象相交于点C,已知 , 点C的横坐标为2.
23. 如图,在平面直角坐标系中,直线与 , 轴分别相交于点A,B,与反比例函数的图象相交于点C,已知 , 点C的横坐标为2. (1)、求 , 的值;(2)、平行于轴的动直线与和反比例函数的图象分别交于点D,E,若以B,D,E,O为顶点的四边形为平行四边形,求点D的坐标.
(1)、求 , 的值;(2)、平行于轴的动直线与和反比例函数的图象分别交于点D,E,若以B,D,E,O为顶点的四边形为平行四边形,求点D的坐标.

