浙江省2023年数学六年级下学期期末质量检测模拟卷（一）
试卷更新日期：2023-06-15 类型：期末考试
一、单选题
-
1. 一件商品原来的价格是600元，商场促销期间推出“每满500元减180元”的活动，这件商品相当于按原来价格的（ ）出售。A、三折 B、三六折 C、六四折 D、七折2. 某品牌SUV汽车三月份的产量比二月份增长了-2.5%，“-2.5%”表示（ ）。A、增长了2.5% B、下降了2.5% C、不增不降 D、无法确定3. 为防控新冠病毒感染，尽量避免外出，人员聚集，网上购物数量增多。某县2022年12月份的快递数量达到15万件，比11月份的快递数量增长了二成半。11月份的快递数量是多少万件？正确的算式是（ ）A、15÷25% B、15÷（1+25%） C、15÷（1﹣25%） D、15×（1﹣25%）4. 有两个相关联的量，它们的关系如下图所示，这两个量可以是（ ）。
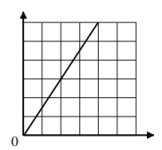A、圆的半径和面积 B、正方形的周长和边长 C、一个人的身高和他的年龄 D、路程一定，行驶的速度和时间5. 在比例尺为1：5000000的地图上量得甲乙两地的距离是8.4厘米，如果一辆汽车以每小时60千米的速度从甲地开出，16时到达乙地，这辆汽车是上午（ ）出发的．A、8时 B、9时 C、10时 D、11时6. 李叔叔要给房子的四面涂上颜色，但不管怎么设计，总是至少有两面墙是同一种颜色，李叔叔可能买了（ ）种不同颜色的涂料。A、3 B、4 C、5 D、67. 根据下面的实验，可知水面下降了（ ）cm。
A、1.5 B、4.5 C、6 D、188. 两支规格不同的蜡烛，长的能燃烧7小时，短的能燃烧10小时，同时点燃4小时后，两支蜡烛剩下的长度相同，原来短蜡烛的长度与长蜡烛的长度之比是（ ）。A、7：10 B、3：5 C、4：7 D、5：79. 李晓红放学后先到书店买书，再回家。如图两图记录了她的行程。李晓红从学校到家一共用了（ ）分钟。
A、30 B、36 C、32 D、2810. 一个圆柱，如果底面直径增加2厘米，侧面积就增加62.8平方厘米；如果高增加2厘米，侧面积就增加37.68平方厘米。这个圆柱的体积是（ ）立方厘米。A、60π B、90π C、160π D、120π二、填空题
-
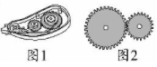
11. =0.75=：=15÷=%＝折。12. 王叔叔买体育彩票中奖500万，按税法规定，取得偶然所得的个人为个人所得税的纳税义务人，应依法纳税。偶然所得以收入金额为应纳税所得额，纳税率为20％，根据规定，王叔叔应纳税元，实际拿元。13. 如果 ， 那么x和y成比例；如果 ， 那么x和y成比例。14. 一件服装标价200元，按标价的八折销售，该服装卖元。一个书包，打九折后售价45元，原价元。15. 如图1，修正带是通过两个齿轮的相互咬合进行工作的，其原理可简化为图2所示模型。大齿轮的直径是4cm，小齿轮的直径是2.6cm，如果小齿轮转20圈，那么大齿轮转圈。
16. 从6：00到9：00，时针在钟面上旋转了度；从3：15到3：45，分针在钟面上旋转了度。17. 王大伯共种了27垄大白菜，已经收了5垄，产量分别是：103千克、99千克、100千克、97千克、101千克，按这5垄的平均产量算，王大伯家今年可以收大白菜千克。18. 美术课上，张老师教同学们用一张长方形卡纸做成一个圆柱。先把长方形卡纸剪成两个大小相等的圆和一个长方形（如图），分别作圆柱的底面和侧面，通过粘合就成了一个圆柱。这个圆柱表面积是cm2 ， 体积是cm3。（接头与卡纸的厚度不计）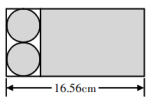
19. 蜀锦为中国四大名锦之一，是一种具有两千多年历史的丝织品。一匹蜀锦长3米，先用去 ， 再用去余下的米，还剩下米。20. 李军一家三口随团旅游，他把旅途的费用支出情况制成了如图所示的统计图，若他们食宿花了1500元，购物占总支出的25%，购物花去元。路费占总支出的%，比食宿支出多%，食宿支出比购物支出多总支出的%。
21. 如图，淘气把若干个完全一样的梯形拼起来，当拼成图形的周长是100厘米时，共需要 个这样的梯形。（单位：厘米）
22. 如上图，甲圆柱形容器是空的，乙长方形容器中水深6.28cm，要将乙容器中的水全部倒入甲容器，这时水深cm，如果倒入与这个圆柱底面积之比是5∶1的圆锥形容器中水面高cm。
三、作图题
-
23. 在下面的方格中按要求画一画，标一标（每个小方格的边长均为1cm）。
(1)、画出三角形ABC绕点B逆时针旋转90°后的图形。(2)、画出正方形按3：1的比放大后的图形。(3)、点D的位置用数对表示是（16，1），点E的位置用数对表示是（12，1），点F在点D的北偏西45度方向，且点F与点E相距4cm，请在图中标出点E和点F的位置。四、计算题
-
24. 直接写出得数
÷3= 0.88+1.22= ＋25%= 5－-= 1÷+÷1=
10－20%＝ 0÷1＝ 0.9×＝ 1-+= 1.25×4×2.5×8=
25. 下面各题能简便计算要简算①5.7×+1.3÷
②（+﹣）÷
③÷8×（÷）
④32÷32
⑤7.75×+25%×0.125
⑥73×25%+×26+0.25
26. 解比例(1)、 =(2)、 ：=：x(3)、40∶＝2.5∶15(4)、0.5∶x=27. 如图，平行四边形底是15厘米，底边上的高是10厘米，四个圆的半径是3厘米，圆心都在平行四边形的顶点上，求平行四边形内空白部分的面积。
五、解答题
-
28. 六年级进行“科技小发明”比赛，六（1）班同学上交了36幅作品，比六（2）班上交的少 ， 这两个班共上交了多少幅作品？29. 同学们，你们听说过勾股定理吗？它主要的结论是在直角三角形中，两条直角边的平方之和等于斜边的平方，如图1中可得：a2+b2＝c2 ， 反过来也可以说如果围成三角形的三根小棒的长度是a、b、c，只要符合a2+b2＝c2 ， 这个三角形就一定是直角三角形。
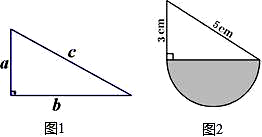(1)、用6cm、8cm、10cm三根小棒能围成一个三角形；我还能想象：用6cm、8cm、9cm三根小棒能围成一个三角形。（填“直角”“锐角”或“钝角”）(2)、求图2阴影部分的面积。30. 目前居民使用的是普通电表，电价是0.52元/千瓦时。为了倡导建设“节约型社会”，鼓励居民安装分时电表实行峰谷电价，具体收费标准如下：时段
峰时（8：00﹣21：00）
谷时（21：00﹣次日8：00）
每千瓦时电价（元）
0.55
0.35
淘气家一个月大约用电160千瓦时，其中谷时用电量是一个月总用电量的。淘气家改用分时电表合算吗？（请通过计算说明理由）
31. 上科学课时，陈老师与同学们一起做实验。一个无水的长方体水槽（如图）。有一个水龙头从10：00开始向水槽内注水，水的流量为1200立方厘米/分。10：05关闭水龙头停止流水。
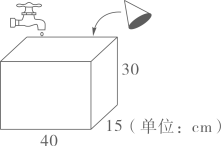(1)、10：05时水槽的水面高度为多少厘米？(2)、如果在水槽内放入一个高为9厘米的圆锥铁块，全部浸没于水中，这时水面升高了2厘米，这个圆锥铁块的体积是多少？32. 近些年，新能源汽车以其清洁环保、使用成本低、高能源利用率等优点，慢慢走进人们的生活，如图是我国某区域2021年各季度新能源汽车销售量情况统计图。
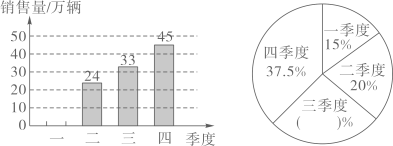(1)、这个区域2021年共销售新能源汽车 万辆，其中一季度销售 万辆。(2)、将上面的条形统计图和扇形统计图中缺失的数据填、画完整。(3)、结合以上信息，请你预测2022年这个区域新能源汽车的销售量可能是 万辆。将你预测的理由写在下面。33. 东东和明明共有邮票56张，东东邮票张数的和明明邮票张数的相等。东东和明明各有邮票多少张？下面是小军和小红的做法：
小军：
东东：56÷（3+4）×3＝24（张）
明明：56÷（3+4）×4＝32（张）
小红：
解：设东东有邮票x张，那么明明有邮票（56﹣x）张。
x+（56﹣x）＝56
(1)、小军和小红做得有道理吗？请你解释他们的想法。(2)、你还有其它方法吗？写出来。
-