重庆市2023年中考数学试卷(A卷)
试卷更新日期:2023-06-15 类型:中考真卷
一、单选题
-
1. 8的相反数是( )A、 B、8 C、 D、2. 四个大小相同的正方体搭成的几何体如图所示,从正面得到的视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、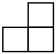 3. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、4. 若两个相似三角形周长的比为 , 则这两个三角形对应边的比是( )A、 B、 C、 D、5. 如图, , 若 , 则的度数为( )
3. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、4. 若两个相似三角形周长的比为 , 则这两个三角形对应边的比是( )A、 B、 C、 D、5. 如图, , 若 , 则的度数为( ) A、 B、 C、 D、6. 估计的值应在( )A、7和8之间 B、8和9之间 C、9和10之间 D、10和11之间7. 用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了9根木棍,第②个图案用了14根木棍,第③个图案用了19根木棍,第④个图案用了24根木棍,……,按此规律排列下去,则第⑧个图案用的木棍根数是( )
A、 B、 C、 D、6. 估计的值应在( )A、7和8之间 B、8和9之间 C、9和10之间 D、10和11之间7. 用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了9根木棍,第②个图案用了14根木棍,第③个图案用了19根木棍,第④个图案用了24根木棍,……,按此规律排列下去,则第⑧个图案用的木棍根数是( ) A、39 B、44 C、49 D、548. 如图,是的切线,为切点,连接 . 若 , , , 则的长度是( )
A、39 B、44 C、49 D、548. 如图,是的切线,为切点,连接 . 若 , , , 则的长度是( )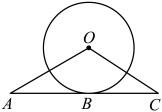 A、 B、 C、 D、9. 如图,在正方形中,点 , 分别在 , 上,连接 , , , . 若 , 则一定等于( )
A、 B、 C、 D、9. 如图,在正方形中,点 , 分别在 , 上,连接 , , , . 若 , 则一定等于( ) A、 B、 C、 D、10. 在多项式(其中)中,对相邻的两个字母间任意添加绝对值符号,添加绝对值符号后仍只有减法运算,然后进行去绝对值运算,称此为“绝对操作”.例如: , , …….
A、 B、 C、 D、10. 在多项式(其中)中,对相邻的两个字母间任意添加绝对值符号,添加绝对值符号后仍只有减法运算,然后进行去绝对值运算,称此为“绝对操作”.例如: , , …….下列说法:
①存在“绝对操作”,使其运算结果与原多项式相等;
②不存在“绝对操作”,使其运算结果与原多项式之和为;
③所有的“绝对操作”共有种不同运算结果.
其中正确的个数是( )
A、 B、 C、 D、二、填空题
-
11. 计算.12. 如图,在正五边形ABCDE中,连接AC,则∠BAC的度数为 .
 13. 一个口袋中有1个红色球,有1个白色球,有1个蓝色球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后放回,摇匀后再从中随机摸出一个球,则两次都摸到红球的概率是 .14. 某新建工业园区今年六月份提供就业岗位个,并按计划逐月增长,预计八月份将提供岗位个.设七、八两个月提供就业岗位数量的月平均增长率为 , 根据题意,可列方程为 .15. 如图,在中, , , 点D为上一点,连接 . 过点B作于点E,过点C作交的延长线于点F.若 , , 则的长度为 .
13. 一个口袋中有1个红色球,有1个白色球,有1个蓝色球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后放回,摇匀后再从中随机摸出一个球,则两次都摸到红球的概率是 .14. 某新建工业园区今年六月份提供就业岗位个,并按计划逐月增长,预计八月份将提供岗位个.设七、八两个月提供就业岗位数量的月平均增长率为 , 根据题意,可列方程为 .15. 如图,在中, , , 点D为上一点,连接 . 过点B作于点E,过点C作交的延长线于点F.若 , , 则的长度为 .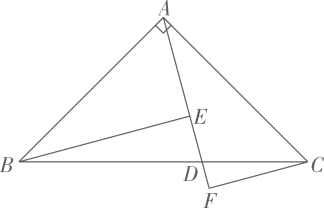 16. 如图,是矩形的外接圆,若 , 则图中阴影部分的面积为 . (结果保留)
16. 如图,是矩形的外接圆,若 , 则图中阴影部分的面积为 . (结果保留) 17. 若关于x的一元一次不等式组 , 至少有2个整数解,且关于y的分式方程有非负整数解,则所有满足条件的整数a的值之和是 .18. 如果一个四位自然数的各数位上的数字互不相等且均不为0,满足 , 那么称这个四位数为“递减数”.例如:四位数4129,∵ , ∴4129是“递减数”;又如:四位数5324,∵ , ∴5324不是“递减数”.若一个“递减数”为 , 则这个数为;若一个“递减数”的前三个数字组成的三位数与后三个数字组成的三位数的和能被9整除,则满足条件的数的最大值是 .
17. 若关于x的一元一次不等式组 , 至少有2个整数解,且关于y的分式方程有非负整数解,则所有满足条件的整数a的值之和是 .18. 如果一个四位自然数的各数位上的数字互不相等且均不为0,满足 , 那么称这个四位数为“递减数”.例如:四位数4129,∵ , ∴4129是“递减数”;又如:四位数5324,∵ , ∴5324不是“递减数”.若一个“递减数”为 , 则这个数为;若一个“递减数”的前三个数字组成的三位数与后三个数字组成的三位数的和能被9整除,则满足条件的数的最大值是 .三、解答题
-
19. 计算:(1)、;(2)、20. 学习了平行四边形后,小虹进行了拓展性研究.她发现,如果作平行四边形一条对角线的垂直平分线,那么这个平行四边形的一组对边截垂直平分线所得的线段被垂足平分.她的解决思路是通过证明对应线段所在的两个三角形全等得出结论.请根据她的思路完成以下作图与填空:
用直尺和圆规,作的垂直平分线交于点E,交于点F,垂足为点O.(只保留作图痕迹)
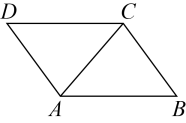
已知:如图,四边形是平行四边形,是对角线,垂直平分 , 垂足为点O.
求证: .
证明:∵四边形是平行四边形,
∴ .
∴ ▲ .
∵垂直平分 ,
∴ ▲ .
又 ▲ .
∴ .
∴ .
小虹再进一步研究发现,过平行四边形对角线中点的直线与平行四边形一组对边相交形成的线段均有此特征.请你依照题意完成下面命题:
过平行四边形对角线中点的直线 ▲ .
21. 为了解A、B两款品质相近的智能玩具飞机在一次充满电后运行的最长时间,有关人员分别随机调查了A、B两款智能玩具飞机各架,记录下它们运行的最长时间(分钟),并对数据进行整理、描述和分析(运行最长时间用x表示,共分为三组:合格 , 中等 , 优等),下面给出了部分信息:A款智能玩具飞机架一次充满电后运行最长时间是:
B款智能玩具飞机架一次充满电后运行最长时间属于中等的数据是:
两款智能玩具飞机运行最长时间统计表,B款智能玩具飞机运行最长时间扇形统计图
类别
A
B
平均数
中位数
b
众数
a
方差

根据以上信息,解答下列问题:
(1)、上述图表中 , , ;(2)、根据以上数据,你认为哪款智能玩具飞机运行性能更好?请说明理由(写出一条理由即可);(3)、若某玩具仓库有A款智能玩具飞机架、B款智能玩具飞机架,估计两款智能玩具飞机运行性能在中等及以上的共有多少架?22. 某公司不定期为员工购买某预制食品厂生产的杂酱面、牛肉面两种食品.(1)、该公司花费3000元一次性购买了杂酱面、牛肉面共170份,此时杂酱面、牛肉面的价格分别为15元、20元,求购买两种食品各多少份?(2)、由于公司员工人数和食品价格有所调整,现该公司分别花费1260元、1200元一次性购买杂酱面、牛肉面两种食品,已知购买杂酱面的份数比牛肉面的份数多 , 每份杂酱面比每份牛肉面的价格少6元,求购买牛肉面多少份?23. 如图,是边长为4的等边三角形,动点E,F分别以每秒1个单位长度的速度同时从点A出发,点E沿折线方向运动,点F沿折线方向运动,当两者相遇时停止运动.设运动时间为t秒,点E,F的距离为y.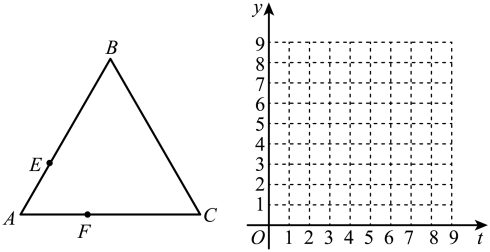 (1)、请直接写出y关于t的函数表达式并注明自变量t的取值范围;(2)、在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;(3)、结合函数图象,写出点E,F相距3个单位长度时t的值.24. 为了满足市民的需求,我市在一条小河两侧开辟了两条长跑锻炼线路,如图;①;② . 经勘测,点B在点A的正东方,点C在点B的正北方千米处,点D在点C的正西方千米处,点D在点A的北偏东方向,点E在点A的正南方,点E在点B的南偏西方向.(参考数据:
(1)、请直接写出y关于t的函数表达式并注明自变量t的取值范围;(2)、在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;(3)、结合函数图象,写出点E,F相距3个单位长度时t的值.24. 为了满足市民的需求,我市在一条小河两侧开辟了两条长跑锻炼线路,如图;①;② . 经勘测,点B在点A的正东方,点C在点B的正北方千米处,点D在点C的正西方千米处,点D在点A的北偏东方向,点E在点A的正南方,点E在点B的南偏西方向.(参考数据: (1)、求AD的长度.(结果精确到1千米)(2)、由于时间原因,小明决定选择一条较短线路进行锻炼,请计算说明他应该选择线路①还是线路②?25. 如图,在平面直角坐标系中,抛物线过点 , 且交x轴于点 , B两点,交y轴于点C.
(1)、求AD的长度.(结果精确到1千米)(2)、由于时间原因,小明决定选择一条较短线路进行锻炼,请计算说明他应该选择线路①还是线路②?25. 如图,在平面直角坐标系中,抛物线过点 , 且交x轴于点 , B两点,交y轴于点C. (1)、求抛物线的表达式;(2)、点P是直线上方抛物线上的一动点,过点P作于点D,过点P作y轴的平行线交直线于点E,求周长的最大值及此时点P的坐标;(3)、在(2)中周长取得最大值的条件下,将该抛物线沿射线方向平移个单位长度,点M为平移后的抛物线的对称轴上一点.在平面内确定一点N,使得以点A,P,M,N为顶点的四边形是菱形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.26. 在中, , , 点为线段上一动点,连接 .
(1)、求抛物线的表达式;(2)、点P是直线上方抛物线上的一动点,过点P作于点D,过点P作y轴的平行线交直线于点E,求周长的最大值及此时点P的坐标;(3)、在(2)中周长取得最大值的条件下,将该抛物线沿射线方向平移个单位长度,点M为平移后的抛物线的对称轴上一点.在平面内确定一点N,使得以点A,P,M,N为顶点的四边形是菱形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.26. 在中, , , 点为线段上一动点,连接 . (1)、如图1,若 , , 求线段的长.(2)、如图2,以为边在上方作等边 , 点是的中点,连接并延长,交的延长线于点 . 若 , 求证: .(3)、在取得最小值的条件下,以为边在右侧作等边 . 点为所在直线上一点,将沿所在直线翻折至所在平面内得到 . 连接 , 点为的中点,连接 , 当取最大值时,连接 , 将沿所在直线翻折至所在平面内得到 , 请直接写出此时的值.
(1)、如图1,若 , , 求线段的长.(2)、如图2,以为边在上方作等边 , 点是的中点,连接并延长,交的延长线于点 . 若 , 求证: .(3)、在取得最小值的条件下,以为边在右侧作等边 . 点为所在直线上一点,将沿所在直线翻折至所在平面内得到 . 连接 , 点为的中点,连接 , 当取最大值时,连接 , 将沿所在直线翻折至所在平面内得到 , 请直接写出此时的值.