重庆市2023年中考数学试卷(B卷)
试卷更新日期:2023-06-15 类型:中考真卷
一、单选题
-
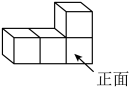
1. 4的相反数是( )A、 B、 C、4 D、2. 四个大小相同的正方体搭成的几何体如图所示,从正面看到的视图是( )
 A、
A、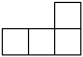 B、
B、 C、
C、 D、
D、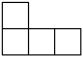 3. 如图,直线 , 被直线所截,若 , , 则的度数为( ).
3. 如图,直线 , 被直线所截,若 , , 则的度数为( ).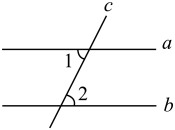 A、 B、 C、 D、4. 如图,已知 , , 若的长度为6,则的长度为( )
A、 B、 C、 D、4. 如图,已知 , , 若的长度为6,则的长度为( ) A、4 B、9 C、12 D、5. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、6. 用圆圈按如图所示的规律拼图案,其中第①个图案中有2个圆圈,第②个图案中有5个圆圈,第③个图案中有8个圆圈,第④个图案中有11个圆圈,…,按此规律排列下去,则第⑦个图案中圆圈的个数为( )
A、4 B、9 C、12 D、5. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、6. 用圆圈按如图所示的规律拼图案,其中第①个图案中有2个圆圈,第②个图案中有5个圆圈,第③个图案中有8个圆圈,第④个图案中有11个圆圈,…,按此规律排列下去,则第⑦个图案中圆圈的个数为( ) A、14 B、20 C、23 D、267. 估计的值应在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间8. 如图,为的直径,直线与相切于点C,连接 , 若 , 则的度数为( )
A、14 B、20 C、23 D、267. 估计的值应在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间8. 如图,为的直径,直线与相切于点C,连接 , 若 , 则的度数为( )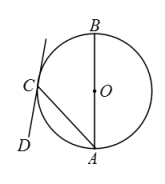 A、 B、 C、 D、9. 如图,在正方形中,O为对角线的中点,E为正方形内一点,连接 , , 连接并延长,与的平分线交于点F,连接 , 若 , 则的长度为( )
A、 B、 C、 D、9. 如图,在正方形中,O为对角线的中点,E为正方形内一点,连接 , , 连接并延长,与的平分线交于点F,连接 , 若 , 则的长度为( )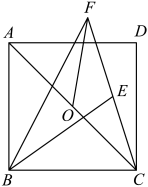 A、2 B、 C、1 D、10. 在多项式(其中)中,对相邻的两个字母间任意添加绝对值符号,添加绝对值符号后仍只有减法运算,然后进行去绝对值运算,称此为“绝对操作”.例如: , , …….
A、2 B、 C、1 D、10. 在多项式(其中)中,对相邻的两个字母间任意添加绝对值符号,添加绝对值符号后仍只有减法运算,然后进行去绝对值运算,称此为“绝对操作”.例如: , , …….下列说法:
①存在“绝对操作”,使其运算结果与原多项式相等;
②不存在“绝对操作”,使其运算结果与原多项式之和为;
③所有的“绝对操作”共有种不同运算结果.
其中正确的个数是( )
A、 B、 C、 D、二、填空题
-
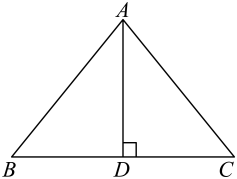
11. 计算: .12. 有四张完全一样正面分别写有汉字“清”“风”“朗”“月”的卡片,将其背面朝上并洗匀,从中随机抽取一张,记下卡片正面上的汉字后放回,洗匀后再从中随机抽取一张,则抽取的两张卡片上的汉字相同的概率是 .13. 若七边形的内角中有一个角为 , 则其余六个内角之和为 .14. 如图,在中, , 是边的中线,若 , , 则的长度为 .
 15. 为了加快数字化城市建设,某市计划新建一批智能充电桩,第一个月新建了301个充电桩,第三个月新建了500个充电桩,设该市新建智能充电桩个数的月平均增长率为 , 根据题意,请列出方程 .16. 如图,在矩形中, , , E为的中点,连接 , 以E为圆心,长为半径画弧,分别与交于点M,N,则图中阴影部分的面积为 . (结果保留)
15. 为了加快数字化城市建设,某市计划新建一批智能充电桩,第一个月新建了301个充电桩,第三个月新建了500个充电桩,设该市新建智能充电桩个数的月平均增长率为 , 根据题意,请列出方程 .16. 如图,在矩形中, , , E为的中点,连接 , 以E为圆心,长为半径画弧,分别与交于点M,N,则图中阴影部分的面积为 . (结果保留)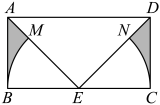 17. 若关于x的不等式组的解集为 , 且关于y的分式方程的解为正数,则所有满足条件的整数a的值之和为 .18. 对于一个四位自然数M,若它的千位数字比个位数字多6,百位数字比十位数字多2,则称M为“天真数”.如:四位数7311,∵ , , ∴7311是“天真数”;四位数8421,∵ , ∴8421不是“天真数”,则最小的“天真数”为;一个“天真数”M的千位数字为a,百位数字为b,十位数字为c,个位数字为d,记 , , 若能被10整除,则满足条件的M的最大值为 .
17. 若关于x的不等式组的解集为 , 且关于y的分式方程的解为正数,则所有满足条件的整数a的值之和为 .18. 对于一个四位自然数M,若它的千位数字比个位数字多6,百位数字比十位数字多2,则称M为“天真数”.如:四位数7311,∵ , , ∴7311是“天真数”;四位数8421,∵ , ∴8421不是“天真数”,则最小的“天真数”为;一个“天真数”M的千位数字为a,百位数字为b,十位数字为c,个位数字为d,记 , , 若能被10整除,则满足条件的M的最大值为 .三、解答题
-
19. 计算:(1)、;(2)、 .20. 学习了平行四边形后,小虹进行了拓展性研究.她发现,如果作平行四边形一条对角线的垂直平分线,那么这个平行四边形的一组对边截垂直平分线所得的线段被垂足平分.她的解决思路是通过证明对应线段所在的两个三角形全等得出结论.请根据她的思路完成以下作图与填空:
用直尺和圆规,作的垂直平分线交于点E,交于点F,垂足为点O.(只保留作图痕迹)
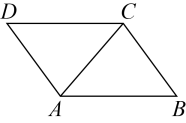
已知:如图,四边形是平行四边形,是对角线,垂直平分 , 垂足为点O.
求证: .
证明:∵四边形是平行四边形,
∴ .
∴ ▲ .
∵垂直平分 ,
∴ ▲ .
又 ▲ .
∴ .
∴ .
小虹再进一步研究发现,过平行四边形对角线中点的直线与平行四边形一组对边相交形成的线段均有此特征.请你依照题意完成下面命题:
过平行四边形对角线中点的直线 ▲ .
21. 某洗车公司安装了 , 两款自动洗车设备,工作人员从消费者对 , 两款设备的满意度评分中各随机抽取20份,并对数据进行整理、描述和分析(评分分数用表示,分为四个等级,不满意 , 比较满意 , 满意 , 非常满意),下面给出了部分信息.抽取的对款设备的评分数据中“满意”包含的所有数据:
83,85,85,87,87,89;
抽取的对款设备的评分数据:
68,69,76,78,81,84,85,86,87,87,87,89,95,97,98,98,98,98,99,100.
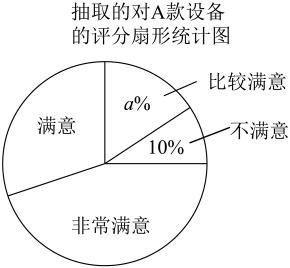
抽取的对 , 款设备的评分统计表
设备
平均数
中位数
众数
“非常满意”所占百分比
88
96
45%
88
87
40%
根据以上信息,解答下列问题:
(1)、填空: , , ;(2)、5月份,有600名消费者对款自动洗车设备进行评分,估计其中对款自动洗车设备“比较满意”的人数;(3)、根据以上数据,你认为哪一款自动洗车设备更受消费者欢迎?请说明理由(写出一条理由即可).22. 如图,是边长为4的等边三角形,动点E,F分别以每秒1个单位长度的速度同时从点A出发,点E沿折线方向运动,点F沿折线方向运动,当两者相遇时停止运动.设运动时间为t秒,点E,F的距离为y.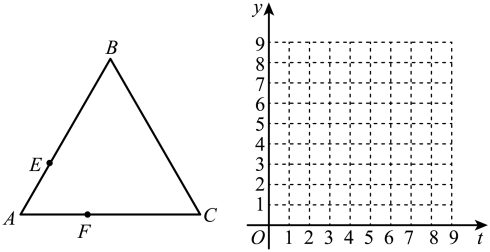 (1)、请直接写出y关于t的函数表达式并注明自变量t的取值范围;(2)、在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;(3)、结合函数图象,写出点E,F相距3个单位长度时t的值.23. 某粮食生产基地为了落实在适宜地区开展双季稻中间季节再种一季油菜的号召,积极扩大粮食生产规模,计划用基地的甲、乙两区农田进行油菜试种.甲区的农田比乙区的农田多10000亩,甲区农田的和乙区全部农田均适宜试种,且两区适宜试种农田的面积刚好相同.(1)、求甲、乙两区各有农田多少亩?(2)、在甲、乙两区适宜试种的农田全部种上油菜后,为加强油菜的虫害治理,基地派出一批性能相同的无人机,对试种农田喷洒除虫药,由于两区地势差别,派往乙区的无人机架次是甲区的1.2倍(每架次无人机喷洒时间相同),喷洒任务完成后,发现派往甲区的每架次无人机比乙区的平均多喷洒亩,求派往甲区每架次无人机平均喷洒多少亩?24. 人工海产养殖合作社安排甲、乙两组人员分别前往海面A,B养殖场捕捞海产品,经测量,A在灯塔C的南偏西方向,B在灯塔C的南偏东方向,且在A的正东方向,米.
(1)、请直接写出y关于t的函数表达式并注明自变量t的取值范围;(2)、在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;(3)、结合函数图象,写出点E,F相距3个单位长度时t的值.23. 某粮食生产基地为了落实在适宜地区开展双季稻中间季节再种一季油菜的号召,积极扩大粮食生产规模,计划用基地的甲、乙两区农田进行油菜试种.甲区的农田比乙区的农田多10000亩,甲区农田的和乙区全部农田均适宜试种,且两区适宜试种农田的面积刚好相同.(1)、求甲、乙两区各有农田多少亩?(2)、在甲、乙两区适宜试种的农田全部种上油菜后,为加强油菜的虫害治理,基地派出一批性能相同的无人机,对试种农田喷洒除虫药,由于两区地势差别,派往乙区的无人机架次是甲区的1.2倍(每架次无人机喷洒时间相同),喷洒任务完成后,发现派往甲区的每架次无人机比乙区的平均多喷洒亩,求派往甲区每架次无人机平均喷洒多少亩?24. 人工海产养殖合作社安排甲、乙两组人员分别前往海面A,B养殖场捕捞海产品,经测量,A在灯塔C的南偏西方向,B在灯塔C的南偏东方向,且在A的正东方向,米.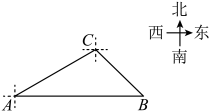 (1)、求B养殖场与灯塔C的距离(结果精确到个位);(2)、甲组完成捕捞后,乙组还未完成捕捞,甲组决定前往B处协助捕捞,若甲组航行的平均速度为600米/每分钟,请计算说明甲组能否在9分钟内到达B处?(参考数据: , )25. 如图,在平面直角坐标系中,抛物线与轴交于点 , , 与轴交于点 , 其中 , .
(1)、求B养殖场与灯塔C的距离(结果精确到个位);(2)、甲组完成捕捞后,乙组还未完成捕捞,甲组决定前往B处协助捕捞,若甲组航行的平均速度为600米/每分钟,请计算说明甲组能否在9分钟内到达B处?(参考数据: , )25. 如图,在平面直角坐标系中,抛物线与轴交于点 , , 与轴交于点 , 其中 , .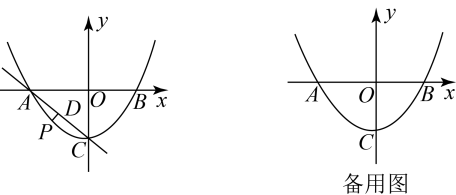 (1)、求该抛物线的表达式;(2)、点是直线下方抛物线上一动点,过点作于点 , 求的最大值及此时点的坐标;(3)、在(2)的条件下,将该抛物线向右平移个单位,点为点的对应点,平移后的抛物线与轴交于点 , 为平移后的抛物线的对称轴上任意一点.写出所有使得以为腰的是等腰三角形的点的坐标,并把求其中一个点的坐标的过程写出来.26. 如图,在等边中,于点 , 为线段上一动点(不与 , 重合),连接 , , 将绕点顺时针旋转得到线段 , 连接 .
(1)、求该抛物线的表达式;(2)、点是直线下方抛物线上一动点,过点作于点 , 求的最大值及此时点的坐标;(3)、在(2)的条件下,将该抛物线向右平移个单位,点为点的对应点,平移后的抛物线与轴交于点 , 为平移后的抛物线的对称轴上任意一点.写出所有使得以为腰的是等腰三角形的点的坐标,并把求其中一个点的坐标的过程写出来.26. 如图,在等边中,于点 , 为线段上一动点(不与 , 重合),连接 , , 将绕点顺时针旋转得到线段 , 连接 .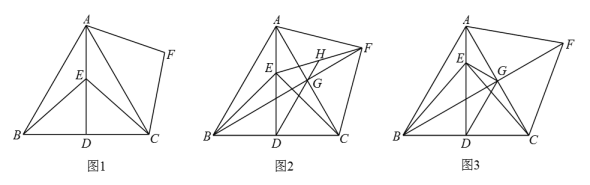 (1)、如图1,求证:;(2)、如图2,连接交于点 , 连接 , , 与所在直线交于点 , 求证:;(3)、如图3,连接交于点 , 连接 , , 将沿所在直线翻折至所在平面内,得到 , 将沿所在直线翻折至所在平面内,得到 , 连接 , . 若 , 直接写出的最小值.
(1)、如图1,求证:;(2)、如图2,连接交于点 , 连接 , , 与所在直线交于点 , 求证:;(3)、如图3,连接交于点 , 连接 , , 将沿所在直线翻折至所在平面内,得到 , 将沿所在直线翻折至所在平面内,得到 , 连接 , . 若 , 直接写出的最小值.