辽宁省锦州市黑山县2022-2023学年七年级下学期期中数学试题

试卷更新日期：2023-06-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 ${(x^{2})}^{3} = x^{5}$ B、 $x + x^{2} = x$ C、 $x \cdot x^{2} = x^{3}$ D、 ${(- 2 x^{2})}^{3} = - 6 x^{6}$

查看试题解析
2. 如图，两条直线交于点 $O$ ，若 $∠ 1 + ∠ 2 = 80 °$ ，则 $∠ 3$ 的度数为（）

A、 $100 °$ B、 $150 °$ C、 $80 °$ D、 $140 °$

查看试题解析
3. 下列等式成立的是（）

A、 $(- x - 1) (- x - 1) = x^{2} - 2 x + 1$ B、 $(- x + 1) (- x + 1) = - x^{2} - 2 x + 1$ C、 $(1 + x) (- x + 1) = 1 - x^{2}$ D、 $(- x + 1) (- x - 1) = - x^{2} - 1$

查看试题解析
4. 如图，将直尺与 $30 °$ 角的三角尺叠放在一起，若 $∠ 1 = 65 °$ ，则 $∠ 2$ 的大小是（）

A、 $45 °$ B、 $55 °$ C、 $65 °$ D、 $75 °$

查看试题解析
5. 近年来，中国北斗芯片实现了22纳米制程的突破，领先GPS芯片. 已知22纳米＝ $0.000 000 022$ 米，数据0.000000022用科学记数法可表示为（）

A、 $0.22 \times 1 0^{- 7}$ B、 $2.2 \times 1 0^{- 8}$ C、 $2.2 \times 1 0^{- 9}$ D、 $22 \times 1 0^{- 9}$

查看试题解析
6. 下列说法中正确的个数有（）
①同位角相等； ②相等的角是对顶角； ③直线外一点到这条直线的垂线段，叫做这个点到这条直线的距离； ④过一点有且只有一条直线与已知直线平行； ⑤不相交的两条直线叫做平行线； ⑥若两条平行线被第三条直线所截，则一组同旁内角的角平分线互相垂直．

A、2个 B、3个 C、4个 D、1个

查看试题解析
7. 如果 $∠ 1$ 与 $∠ 2$ 互余， $∠ 2$ 与 $∠ 3$ 互补，则 $∠ 1$ 与 $∠ 3$ 的关系是（）

A、 $∠ 1 = ∠ 3$ B、 $∠ 1 = ∠ 3 - 90 °$ C、 $∠ 1 = ∠ 3 + 90 °$ D、 $∠ 1 + ∠ 3 = 270 °$

查看试题解析
8. 小亮饭后散步，从家中走20分钟到一个离家900米的报亭看10分钟的报纸后，用15分钟返回家中，下列图形中表示小亮离家的时间与离家的距离之间关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 计算： ${(- 3 a^{2})}^{3} =$ ．

查看试题解析
10. 如图，写出一个能判定 $a ∥ b$ 的条件．

查看试题解析
11. 小明家离学校距离3千米，上学时小明骑自行车以10千米/小时速度走了x 小时，这时离学校还有y千米．写出y与x的函数表达式．

查看试题解析
12. 已知 $(x - 3) (x + 2) = x^{2} + a x + b$ ，则 $a - b$ 的值是．

查看试题解析
13. 已知2^x＝6，4^y＝7，那么2^x+2y的值是．

查看试题解析
14. 如图，直线 $D E$ 与 $∠ A B C$ 的一边 $B C$ 交于点F，写出 $∠ A B C$ 的内错角．

查看试题解析
15. 若多项式x²－6x+m是一个完全平方式，则m＝．

查看试题解析
16. 将一些相同的“O”按如图所示摆放，观察每个图形中的“O”的个数，若第n个图形中“O”的个数是．

查看试题解析

三、解答题

17. 计算

(1)、 ${(2 a x)}^{2} \cdot (- \frac{2}{5} a^{4} x^{3} y^{3}) \div (- \frac{1}{2} a^{5} x y^{2})$ ；

(2)、 ${(2023 - 3.14)}^{0} + 3^{2} - \frac{1}{2} \times {(- \frac{1}{4})}^{- 2}$

(3)、 $2022^{2} - 2020 \times 2024$ （用简便方法计算）；

(4)、 $(x - 3) (2 x + 1) - 3 {(2 x - 1)}^{2}$ ；

(5)、 $(2 x + y + z) (2 x + y - z)$

查看试题解析
18. 先化简，再求值： $[(2 a + b) (2 a - b) - {(2 a - b)}^{2} - b (a - 2 b)] \div (2 a)$ ，其中 $a = \frac{1}{2022}$ ， $b = \frac{2}{3}$ ．

查看试题解析
19. 观察下列各式
（x-1）（x+1）＝ $x^{2}$ -1

（x-1）（ $x^{2}$ +x+1）＝ $x^{3}$ -1

（x-1）（ $x^{3}$ + $x^{2}$ +x+1）＝ $x^{4}$ -1

…

(1)、根据以上规律，则 $(x - 1) (x^{6} + x^{5} + x^{4} + x^{3} + x^{2} + x + 1)$ ＝．

(2)、你能否由此归纳出一般性规律： $(x - 1) (x^{n} + x^{n - 1} + \dots + x^{2} + x + 1)$ ＝．

(3)、根据②求出： $1 + 2 + 2^{2} + \cdot \cdot \cdot + 2^{34} + 2^{35}$ 的结果．

查看试题解析
20.

(1)、如图，利用尺规作图：过点B作BM∥AD（要求：不写作法保留作图痕迹）；

(2)、若直线DE∥AB，设DE与M交于点C，试说明：∠A＝∠BCD

查看试题解析

四、填空题

21. 完成下列填空：
如图，已知AD⊥BC，EF⊥BC，∠1=∠2.试说明：DG∥BA．

解：因为AD⊥BC，EF⊥BC(已知)，

所以∠EFB=∠ADB=90°（     ）．

所以▲∥▲（     ）．

所以∠1=∠BAD（     ）．

又因为∠1=∠2(已知)，

所以▲(等量代换)．

所以DG∥BA（     )．

查看试题解析

五、解答题

22. 如图，是反映一辆出租车从甲地到乙地的速度（千米/时）与时间（分钟）的关系图象；根据图象，回答下列问题：

(1)、汽车从出发到最后停止共经过了多长时间？它的最高时速是多少？

(2)、汽车在哪段时间保持匀速行驶？时速是多少？

(3)、出发后25分钟到30分钟之间可能发生了什么情况？

(4)、用自己的语言大致描述这辆汽车的行驶情况．

查看试题解析
23. 如图，直线 $A B$ ， $C D$ 相交于点O， $∠ B O E = ∠ D O F = 90 °$ ．

(1)、写出 $∠ A O F$ 的所有余角；

(2)、若 $∠ A O F = 69 °$ ，求 $∠ B O F$ 的度数．

查看试题解析
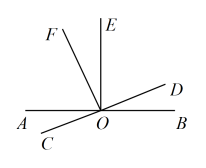24. 问题情境：我们知道，“两条平行线被第三条直线所截，同位角相等，内错角相等，同旁内角互补”，所以在某些探究性问题中通过“构造平行线”可以起到转化的作用．已知三角板 $A B C$ 中， $∠ B A C = 60 °$ ， $∠ B = 30 °$ ， $∠ C = 90 °$ ，长方形 $D E F G$ 中， $D E$ $∥$ $G F$ ．

(1)、问题初探：如图(1)，若将三角板 $A B C$ 的顶点 $A$ 放在长方形的边 $G F$ 上， $B C$ 与 $D E$ 相交于点 $M$ ， $A B ⊥ D E$ 于点 $N$ ，求 $∠ E M C$ 的度数．
分析：过点 $C$ 作 $C H$ $∥$ $G F$ ．则有 $C H$ $∥$ $D E$ ，从而得 $∠ C A F = ∠ H C A$ ， $∠ E M C = ∠ M C H$ ，从而可以求得 $∠ E M C$ 的度数．由分析得，请你直接写出： $∠ C A F$ 的度数为， $∠ E M C$ 的度数为．

(2)、类比再探：若将三角板 $A B C$ 按图（2）所示方式摆放 $(A B$ 与 $D E$ 不垂直 $)$ ，请你猜想写 $∠ C A F$ 与 $∠ E M C$ 的数量关系，并说明理由．

(3)、请你总结（1），（2）解决问题的思路，在图（3）中探究 $∠ B A G$ 与 $∠ B M D$ 的数量关系？并说明理由．

查看试题解析