辽宁省鞍山市岫岩满族自治县联盟校2022-2023学年八年级下学期期中数学试题

试卷更新日期：2023-06-15 类型：期中考试

进入出卷网下载

一、单选题

1. 要使式子 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥1 B、x＜1 C、x≤1 D、x≠1

查看试题解析
2. 下列二次根式中，不能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{8}$ C、 $\sqrt{12}$ D、 $- \sqrt{18}$

查看试题解析
3. 在下列以线段 $a$ 、 $b$ 、 $c$ 的长为三边的三角形中，不能构成直角三角形的是（）

A、 $a = 1.5$ ， $b = 2$ ， $c = 3$ B、 $a = 7$ ， $b = 24$ ， $c = 25$ C、 $a ： b ： c = 3 ： 4 ： 5$ D、 $a = 9$ ， $b = 12$ ， $c = 15$

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{27} \div \sqrt{3} = 3$ B、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ C、 $\sqrt{8} = 4 \sqrt{2}$ D、 $\sqrt{{(- 3)}^{2}} = - 3$

查看试题解析
5. 下列各命题都成立，而它们的逆命题也成立的是（）

A、全等三角形的面积相等 B、对顶角相等 C、如果 $a = b$ ，那么 $| a | = | b |$ D、等腰三角形的两个底角相等

查看试题解析
6. 放学以后，小红和小颖从学校分手，分别沿东南方向和西南方向回家，若小红和小颖行走的速度都是40米/分，小红用15分钟到家，小颖20分钟到家，小红和小颖家的直线距离为（）

A、600米 B、800米 C、1000米 D、不能确定

查看试题解析
7. 如图，下列条件不能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $A B ∥ C D$ ， $A D = B C$ B、 $A B = C D$ ， $A D = B C$ C、 $∠ A B C = ∠ A D C$ ， $∠ B A D = ∠ B C D$ D、 $A O = C O$ ， $B O = D O$

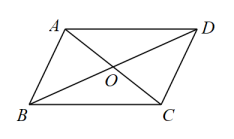查看试题解析
8. 如图，在△ABC中，点D，E分别是边AB，AC的中点，点F是线段DE上的一点连接AF，BF，∠AFB =90°，且AB=8，BC= 14，则EF的长是（）

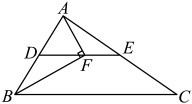A、2 B、3 C、4 D、5

查看试题解析
9. 如图，在平面直角坐标系中，将长方形 $A O C D$ 沿直线 $A E$ 折叠（点E在边 $D C$ 上），折叠后顶点D恰好落在边 $O C$ 上的点F处．若点D的坐标为 $(10 ， 8)$ ．则点E的坐标为（）

A、 $(10 ， 3)$ B、 $(10 ， 4)$ C、 $(10 ， 5)$ D、 $(10 ， 6)$

查看试题解析
10. 在正方形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 交于点 $O$ ， $∠ A D B$ 的平分线交 $A B$ 于点 $E$ ，交 $A C$ 于点 $G$ ．过点 $E$ 作 $E F ⊥ B D$ 于点 $F$ ， $∠ E D M$ 交 $A C$ 于点 $M$ ．下列结论：① $A D = (\sqrt{2} + 1) A E$ ；②四边形 $A E F G$ 是菱形；③ $B E = 2 O G$ ；④若 $∠ E D M = 45 °$ ，则 $G F = C M$ ．其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算： $\sqrt{{(- 2)}^{2}}$ ＝．

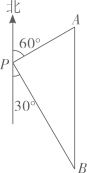
查看试题解析
12. 已知n为正整数， $\sqrt{12 n}$ 也是正整数，那么满足条件n的最小值是．

查看试题解析
13. 如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为30海里的A处，轮船沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则此时轮船所在位置B处与灯塔P之间的距离为．

查看试题解析
14. 如图，在 $▱ A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ， $△ B O C$ 的周长比 $△ B O A$ 的周长大2，若 $B C = 10$ ，则 $A B$ 的长是．

查看试题解析
15. 已知菱形ABCD的边长为6， $∠ A = 60 °$ ，如果点P是菱形内一点，且 $P B = P D = 2 \sqrt{3}$ ，那么 $A P$ 的长为.

查看试题解析
16. 一组正方形按如图所示的方式放置，其中顶点 $B_{1}$ 在 $y$ 轴上，顶点 $C_{1}$ ， $E_{1}$ ， $E_{2}$ ， $C_{2}$ ， $E_{3}$ ， $E_{4}$ ， $C_{3}$ …在 $x$ 轴上，已知正方形 $A_{1} B_{1} C_{1} D_{1}$ 的边长为1， $∠ B_{1} C_{1} O = 60 °$ ， $B_{1} C_{1} ∥ B_{2} C_{2} ∥ B_{3} C_{3}$ ，则正方形 $A_{2023} B_{2023} C_{2023} D_{2023}$ 的边长是．

查看试题解析

三、解答题

17. 计算：

(1)、 $(\sqrt{45} + \sqrt{18}) - (\sqrt{8} - \sqrt{125})$

(2)、 $\sqrt{48} \div (- \sqrt{3}) - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24}$

查看试题解析
18. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点，小明以格点为顶点画出了 $△ A B C$ ．

(1)、小华看了看说， $△ A B C$ 是直角三角形，你同意他的观点吗？说明理由．

(2)、在 $△ A B C$ 中，求 $A C$ 边上高的长．

查看试题解析
19. 如图，已知在▱ABCD中，点E在AB上，点F在CD上，且 $D E ∥ B F$ ，求证： $B E = D F$ ．

查看试题解析
20. 已知 $x = 2 + \sqrt{3}$ ， $y = 2 - \sqrt{3}$ ．

(1)、试求 $x^{2} + y^{2}$ 的值；

(2)、试求 $\frac{x}{y} - \frac{y}{x}$ 的值．

查看试题解析
21. 海滨公园是珠海市市民放风筝的最佳场所，某校八年级（1）班的小华和小轩学习了“勾股定理”之后，为了测得风筝的垂直高度 $C E$ ，他们进行了如下操作：①测得水平距离 $B D$ 的长为12米；②根据手中剩余线的长度计算出风筝线 $B C$ 的长为20米；③牵线放风筝的小明的身高为1.62米．

(1)、求风筝的垂直高度 $C E$ ；

(2)、如果小明想风筝沿 $C D$ 方向下降11米，则他应该往回收线多少米？

查看试题解析
22. 如图，在四边形ABCD中，对角线AC ， BD相交于点O ， AO＝CO ， BO＝DO ，且∠ABC+∠ADC＝180°．

(1)、求证：四边形ABCD是矩形；

(2)、若∠ADF：∠FDC＝3：2，DF⊥AC ，求∠BDF的度数．

查看试题解析
23. 如图，在四边形 $A B C D$ 中，已知 $∠ B = 90 °$ ， $∠ A C B = 30 °$ ， $A B = 3$ ， $A D = 10$ ， $C D = 8$ .

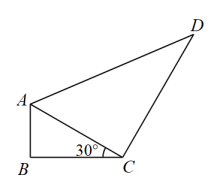(1)、求证： $△ A C D$ 是直角三角形

(2)、求四边形 $A B C D$ 的面积.

查看试题解析
24. 如图，在矩形 $A B C D$ 中，点O是对角线 $A C$ 的中点，过点O作 $E F ⊥ A C$ 交 $B C$ 于点E，交 $A D$ 于F，连接 $A E$ ， $C F$ ．

(1)、求证：四边形 $A E C F$ 是菱形；

(2)、若 $A F = 13$ ， $A C = 24$ ，求四边形 $A E C F$ 的周长和面积．

查看试题解析
25. 如图1，四边形ABCD为正方形，E为对角线 AC上一点，连接DE，BE．

(1)、求证∶BE=DE；

(2)、如图2过点E作EF⊥DE，交边 BC于点F，以DE，EF为邻边作矩形DEFG，连接CG．
①求证∶矩形DEFG是正方形；

②若正方形 ABCD的边长为9，CG=3 $\sqrt{2}$ ，求正方形 DEFG的边长．

查看试题解析