江苏省扬州市宝应县2022-2023学年八年级上学期期中数学试题
试卷更新日期:2023-06-15 类型:期中考试
一、单选题
-
1. 下列图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下面各图中所给数据的三角形,则甲、乙、丙三个三角形和左侧全等的是( )
2. 下面各图中所给数据的三角形,则甲、乙、丙三个三角形和左侧全等的是( )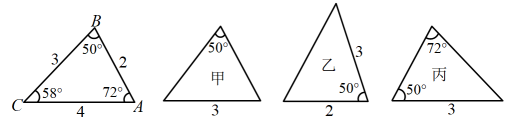 A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙3. 下列计算正确的是( )A、 B、 C、 D、4. 估计 的值在( )A、4和5之间 B、3和4之间 C、2和3之间 D、1和2之间5. 如图,中, , 点在上, , 若 , 则的度数是( )
A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙3. 下列计算正确的是( )A、 B、 C、 D、4. 估计 的值在( )A、4和5之间 B、3和4之间 C、2和3之间 D、1和2之间5. 如图,中, , 点在上, , 若 , 则的度数是( ) A、 B、 C、 D、6. 如图, , 平分 , D是的中点, , 则( )
A、 B、 C、 D、6. 如图, , 平分 , D是的中点, , 则( )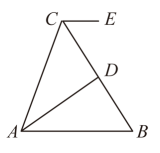 A、 B、 C、 D、7. 用尺规作一个角的角平分线,下列作法中错误的是( )A、
A、 B、 C、 D、7. 用尺规作一个角的角平分线,下列作法中错误的是( )A、 B、
B、 C、
C、 D、
D、 8. 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( )
8. 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( ) A、10 B、 C、10或 D、10或
A、10 B、 C、10或 D、10或二、填空题
-
9. 计算:.10. 如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=度.
 11. 如图,点B、F、C、E在一条直线上, , , 若用“”判定 , 则添加的一个条件是 .
11. 如图,点B、F、C、E在一条直线上, , , 若用“”判定 , 则添加的一个条件是 . 12. 要使式子 有意义,则x的取值范围是 .13. 如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为.
12. 要使式子 有意义,则x的取值范围是 .13. 如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为. 14. 已知一个三角形的三边长分别是4cm、7cm、6cm,该三角形的形状(填“是”或“不是”)直角三角形.15. 已知直角三角形斜边上的中线是2.5cm,斜边上的高是2cm,则这个直角三角形的面积是cm2 .16. 如图,等腰中, , 平分 , 于 , 若 , 则的周长是 .
14. 已知一个三角形的三边长分别是4cm、7cm、6cm,该三角形的形状(填“是”或“不是”)直角三角形.15. 已知直角三角形斜边上的中线是2.5cm,斜边上的高是2cm,则这个直角三角形的面积是cm2 .16. 如图,等腰中, , 平分 , 于 , 若 , 则的周长是 . 17. 已知m为正整数,若是整数,则根据可知m有最小值 . 设n为正整数,若是大于1的整数,则n的最小值为 .18. 等腰中, , 顶角A为 , 平面内有一点P,满足且 , 则的度数为 .
17. 已知m为正整数,若是整数,则根据可知m有最小值 . 设n为正整数,若是大于1的整数,则n的最小值为 .18. 等腰中, , 顶角A为 , 平面内有一点P,满足且 , 则的度数为 .三、解答题
-
19. 求下列各式中x的值.(1)、 ;(2)、 ;20. 如图,点A、D、C、F在同一条直线上, , . 有下列三个条件:① , ② , ③ .
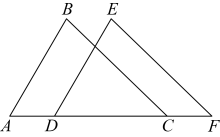 (1)、请在上述三个条件中选取一个条件(填写序号,多选不得分),使得 , 依据是(填“”或“”);(2)、请完成(1)的证明.21. 图1、图2、图3均是5×5的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
(1)、请在上述三个条件中选取一个条件(填写序号,多选不得分),使得 , 依据是(填“”或“”);(2)、请完成(1)的证明.21. 图1、图2、图3均是5×5的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹. (1)、网格中的形状是;(2)、在图1中确定一点D,连接 , 使与全等但不成轴对称;(3)、在图2中确定一点D,连接 , 使与成轴对称;(4)、在图3中边上找一个点D,使得它与点与点构成的三角形为等腰三角形.22. 如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示, , , , , 求 .
(1)、网格中的形状是;(2)、在图1中确定一点D,连接 , 使与全等但不成轴对称;(3)、在图2中确定一点D,连接 , 使与成轴对称;(4)、在图3中边上找一个点D,使得它与点与点构成的三角形为等腰三角形.22. 如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示, , , , , 求 .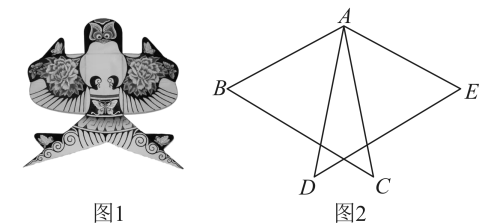 23. 如图是钉板示意图,相邻的两个钉点是边长为1个单位长的小正方形顶点,钉点A、B的连线与钉点C、D的连线交于点E.
23. 如图是钉板示意图,相邻的两个钉点是边长为1个单位长的小正方形顶点,钉点A、B的连线与钉点C、D的连线交于点E. (1)、求证:;(2)、 .24. 如图,在中,的垂直平分线交于点 , 交于点 , 于 , .
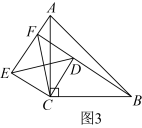
(1)、求证:;(2)、 .24. 如图,在中,的垂直平分线交于点 , 交于点 , 于 , . (1)、求证:为线段的中点.(2)、若 , 求的度数.25. 已知m是144的平方根,n是125的立方根.(1)、求m、n的值;(2)、求的平方根.26. 如图,是等边三角形,D、E分别是边、上的点,且 , 且、交于点G,且 , 垂足为F.
(1)、求证:为线段的中点.(2)、若 , 求的度数.25. 已知m是144的平方根,n是125的立方根.(1)、求m、n的值;(2)、求的平方根.26. 如图,是等边三角形,D、E分别是边、上的点,且 , 且、交于点G,且 , 垂足为F.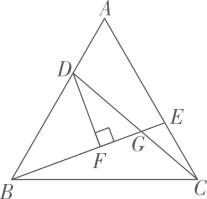 (1)、求证:;(2)、若 , 求DG的长度.27. 在中, , 点E在边上,连结 , 将沿翻折使得点D落在边上得 , 连结 .
(1)、求证:;(2)、若 , 求DG的长度.27. 在中, , 点E在边上,连结 , 将沿翻折使得点D落在边上得 , 连结 . (1)、如图1, , , 求的度数.(2)、如图2,若 , , 求的度数.28. 某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形和等腰直角三角形 , 按如图1的方式摆放, . 该数学兴趣小组进行如下探究,请你帮忙解答:(1)、【初步探究】如图1,试探究与的位置关系,并说明理由;
(1)、如图1, , , 求的度数.(2)、如图2,若 , , 求的度数.28. 某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形和等腰直角三角形 , 按如图1的方式摆放, . 该数学兴趣小组进行如下探究,请你帮忙解答:(1)、【初步探究】如图1,试探究与的位置关系,并说明理由; (2)、【深入探究】如图2,当、、三点共线时,请探究此位置时线段、、之间的数量关系,并说明理由;
(2)、【深入探究】如图2,当、、三点共线时,请探究此位置时线段、、之间的数量关系,并说明理由; (3)、【拓展延伸】如图3,当、、三点不共线时,连接 , 延长交于点 , 连接 , 请猜想此位置时线段、、之间的数量关系: .
(3)、【拓展延伸】如图3,当、、三点不共线时,连接 , 延长交于点 , 连接 , 请猜想此位置时线段、、之间的数量关系: .