江苏省宿迁市泗阳县2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-06-15 类型:期中考试
一、单选题
-
1. 下面图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、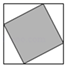 C、
C、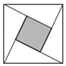 D、
D、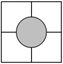 2. 下列调查中,适宜采用普查方式的是( )A、防疫期间,进入校园要测量体温 B、了解全国八年级学生对新冠肺炎病毒的认知情况 C、考察线上学习期间全市中小学生作业完成情况 D、了解全市中学生在疫情期间的作息情况3. 下列分式中是最简分式的是( )A、 B、 C、 D、4. 下列事件中是不可能事件的是( )A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨5. 菱形具有而平行四边形不一定具有的性质是( )A、对角相等 B、对边相等 C、邻边相等 D、对边平行6. 下列运算中正确的是( )A、 B、 C、 D、7. 已知平行四边形中, , 则的度数为( )A、 B、 C、 D、8. 下列条件中,不能判定四边形ABCD是平行四边形的是( )A、 B、 C、 D、9. 为了了解三中九年级840名学生的体重情况,从中抽取100名学生的体重进行分析.在这项调查中,样本是指( )A、840名学生 B、被抽取的100名学生 C、840名学生的体重 D、被抽取的100名学生的体重10. 把分式 , 中a、b、c的值都扩大为原来的2倍,那么分式的值( )A、变为原来的2倍 B、变为原来的4倍 C、变为原来的 D、不变11. 在一个不透明的盒子里装有若干个白球和15个红球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到红球的频率稳定在0.6左右,则袋中白球约有( )A、5个 B、10个 C、15个 D、25个12. 如图,正方形的边长为1,点E是边AD上一点,且 , 点F是边上一个动点,连接EF,以为边作菱形 , 且 , 连接 , 点P为的中点,在点F从点A运动到点B的过程中,点运动所走的路径长为( )
2. 下列调查中,适宜采用普查方式的是( )A、防疫期间,进入校园要测量体温 B、了解全国八年级学生对新冠肺炎病毒的认知情况 C、考察线上学习期间全市中小学生作业完成情况 D、了解全市中学生在疫情期间的作息情况3. 下列分式中是最简分式的是( )A、 B、 C、 D、4. 下列事件中是不可能事件的是( )A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨5. 菱形具有而平行四边形不一定具有的性质是( )A、对角相等 B、对边相等 C、邻边相等 D、对边平行6. 下列运算中正确的是( )A、 B、 C、 D、7. 已知平行四边形中, , 则的度数为( )A、 B、 C、 D、8. 下列条件中,不能判定四边形ABCD是平行四边形的是( )A、 B、 C、 D、9. 为了了解三中九年级840名学生的体重情况,从中抽取100名学生的体重进行分析.在这项调查中,样本是指( )A、840名学生 B、被抽取的100名学生 C、840名学生的体重 D、被抽取的100名学生的体重10. 把分式 , 中a、b、c的值都扩大为原来的2倍,那么分式的值( )A、变为原来的2倍 B、变为原来的4倍 C、变为原来的 D、不变11. 在一个不透明的盒子里装有若干个白球和15个红球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到红球的频率稳定在0.6左右,则袋中白球约有( )A、5个 B、10个 C、15个 D、25个12. 如图,正方形的边长为1,点E是边AD上一点,且 , 点F是边上一个动点,连接EF,以为边作菱形 , 且 , 连接 , 点P为的中点,在点F从点A运动到点B的过程中,点运动所走的路径长为( ) A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
13. 分式 在实数范围内有意义,则x的取值范围是 .14. 一只不透明的袋子里装有4个红球,1个白球.每个球除颜色外都相同,则事件“从中任意摸出1个球,是白球”的事件类型是 . (填“随机事件”“不可能事件”或“必然事件”)15. 如图,菱形的面积为120cm2 , 正方形的面积为50cm2时,则菱形的边长为cm.
 16. 若分式 的值为0,则x的值为 .17. 如图,矩形中, , 对角线相交于点O,点P是线段上任意一点(点Р不与A、D重合),过P作于点E,于点F,则等于 .
16. 若分式 的值为0,则x的值为 .17. 如图,矩形中, , 对角线相交于点O,点P是线段上任意一点(点Р不与A、D重合),过P作于点E,于点F,则等于 . 18. 有六张卡片(形状、大小、质地都相同),正面分别画有下列图形:①线段;②矩形:③平行四边形;④圆:⑤菱形;⑥等边三角形,将卡片背面朝上洗匀,从中抽取一张,其正面图形既是轴对称图形,又是中心对称图形的概率是 .19. 如图,点G在正方形的边上,以为边在正方形外部作正方形 , 连接BF,P、Q分别是、的中点,连接 . 若 , , 则 .
18. 有六张卡片(形状、大小、质地都相同),正面分别画有下列图形:①线段;②矩形:③平行四边形;④圆:⑤菱形;⑥等边三角形,将卡片背面朝上洗匀,从中抽取一张,其正面图形既是轴对称图形,又是中心对称图形的概率是 .19. 如图,点G在正方形的边上,以为边在正方形外部作正方形 , 连接BF,P、Q分别是、的中点,连接 . 若 , , 则 . 20. 如图,平行四边形中, , 以为边作正方形 , 再以为边作正方形 , 若正方形的面积为46,则正方形的面积为 .
20. 如图,平行四边形中, , 以为边作正方形 , 再以为边作正方形 , 若正方形的面积为46,则正方形的面积为 .
三、解答题
-
21. 计算:(1)、(2)、22. 先化简,再求值: , 其中 .23. 如图,转盘被平均分成8个区域,每个区域分别标注数字1、2、3、4、5、6、7、8,任意转动转盘一次,规定:如果指针恰好指在分割线上,那么重转一次,直到指针指向一个标有数字的区域为止.写出下列事件发生的概率:
①P(指针落在标有7的区域);
②P(指针落在标有10的区域);
③P(指针落在标有3的倍数的区域);
以上事件中,是随机事件,是确定事件.(填序号)
 24. 某中学为了解学生每周的课外阅读时间情况,随机抽查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并制成如图所示的不完整的频数分布直方图和扇形统计图.
24. 某中学为了解学生每周的课外阅读时间情况,随机抽查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并制成如图所示的不完整的频数分布直方图和扇形统计图. (1)、被抽样的学生总数有 人,并补全频数分布直方图;(2)、扇形统计图中m的值为 , “E组”对应的圆心角是度;(3)、请估计该校2000名学生中每周的课外阅读时间不少于4小时的学生人数.25. 如图,已知平行四边形的对角线、交于点O,且 .
(1)、被抽样的学生总数有 人,并补全频数分布直方图;(2)、扇形统计图中m的值为 , “E组”对应的圆心角是度;(3)、请估计该校2000名学生中每周的课外阅读时间不少于4小时的学生人数.25. 如图,已知平行四边形的对角线、交于点O,且 . (1)、求证:平行四边形是菱形;(2)、F为上一点,连接交于E,且 , 若 , 求的长.26. 如图1,将两个完全相同的三角形纸片和重合放置,其中 , . 若固定 , 将绕点C顺时针旋转 .
(1)、求证:平行四边形是菱形;(2)、F为上一点,连接交于E,且 , 若 , 求的长.26. 如图1,将两个完全相同的三角形纸片和重合放置,其中 , . 若固定 , 将绕点C顺时针旋转 . (1)、如图2,在旋转的过程中,当点D恰好落在边上时,;(2)、当时,如图3,
(1)、如图2,在旋转的过程中,当点D恰好落在边上时,;(2)、当时,如图3,①小明同学猜想:的面积与的面积相等,试判断小明同学的猜想是否正确,若正确,请你证明小明同学的猜想.若不正确,请说明理由.
②小华同学若将线段的中点G、H、M、N依次连接起来,得到四边形 , 则四边形是▲形.
27. 如图1,直线与轴交于点 , 与轴交于点 , 点在线段上,以为对角线作正方形 , 点刚好落在线段上. (1)、求正方形的边长;(2)、如图2,将正方形沿着轴负方向平移得到正方形 , 当边刚好经过点时,求平移的距离;(3)、若点在坐标轴上,点在直线上,是否存在以点、、、为顶点且以为边的四边形是平行四边形?若存在,直接写出所有满足条件的点的坐标,若不存在,请说明理由.28. 苏科版八下数学教材中,对正方形的性质和判定进行了探究,同时课本94页第19题对正方形中特殊线段的位置和数量关系也进行了探究,在此,我们也来作进一步的探究,如图1,探究所提供的正方形的边长都为2.
(1)、求正方形的边长;(2)、如图2,将正方形沿着轴负方向平移得到正方形 , 当边刚好经过点时,求平移的距离;(3)、若点在坐标轴上,点在直线上,是否存在以点、、、为顶点且以为边的四边形是平行四边形?若存在,直接写出所有满足条件的点的坐标,若不存在,请说明理由.28. 苏科版八下数学教材中,对正方形的性质和判定进行了探究,同时课本94页第19题对正方形中特殊线段的位置和数量关系也进行了探究,在此,我们也来作进一步的探究,如图1,探究所提供的正方形的边长都为2. (1)、【探究】
(1)、【探究】
如图2,在正方形中,如果点E、F分别在、上,且 , 垂足为M,那么与相等吗?证明你的结论.(2)、【应用】
如图3,在正方形中,动点E、F分别在边、上,将正方形沿直线折叠,使点B对应的点M始终落在边上(点M不与点A、D重合),点C落在点N处,与交于点P,设 , 求线段的长(用含t的式子表示).(3)、【拓展】
如图4,在正方形中,E是的中点,F、G分别是、上的动点,且 , 求的最小值.