江苏省苏州市2022-2023学年七年级下学期期中数学试题

试卷更新日期：2023-06-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $2 a + 3 a = 5 a^{2}$ B、 $a^{2} \cdot a^{4} = a^{8}$ C、 ${(- 2 a^{2})}^{3} = - 6 a^{6}$ D、 ${(- a^{3})}^{2} = a^{6}$

查看试题解析
2. 清代诗人袁枚创作了一首诗《苔》：“白日不到处，青春恰自来．苔花如米小，也学牡丹开．”歌颂了苔在恶劣环境下仍有自己的生命意向．若苔花的花粉粒直径线约为0.0000084米，用科学记数法表示 $0.0000084 = 8.4 \times 10^{n}$ ，则n为（）

A、-5 B、5 C、-6 D、6

查看试题解析
3. 若一个多边形的每一个外角都是 $36 °$ ，则这个多边形的边数是（）

A、7 B、8 C、9 D、10

查看试题解析
4. 若 $(y^{2} + a y + 2) (2 y - 4)$ 的结果中不含 $y^{2}$ 项，则a的值为（）

A、0 B、2 C、 $\frac{1}{2}$ D、-2

查看试题解析
5. 如图，是可调躺椅示意图，AE与BD的交点为C，且 $∠ A$ ， $∠ B$ ， $∠ E$ 保持不变．为了舒适，需调整 $∠ D$ 的大小，使 $∠ E F D = 11 0^{∘}$ ．根据图中数据信息，下列调整 $∠ D$ 大小的方法正确的是（）

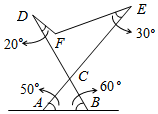A、增大10° B、减小10° C、增大15° D、减小15°

查看试题解析
6. 已知 $a^{2} + a - 5 = 0$ ，代数式 $(a^{2} - 5) (a + 1)$ 的值是（）

A、4 B、-5 C、5 D、-4

查看试题解析
7. 如图，在 $△ A B C$ 中，点D是边BC的中点， $C E = \frac{1}{4} A C$ ， $△ A B C$ 的面积是4，则下列结论正确的是（）

A、 $S_{1} = S_{2}$ B、 $S_{1} = 2$ C、 $S_{2} = 0.5$ D、 $S_{1} - S_{2} = 1$

查看试题解析
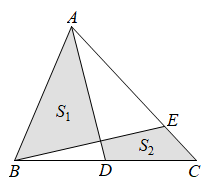8. 如图， $A B ∥ E F$ ， $∠ B A C$ 与 $∠ C D E$ 的角平分线交于点G，且 $G F ∥ D E$ ，已知 $∠ A C D =90 °$ ，若 $∠ A G D = α$ ， $∠ G F E = β$ ，则下列等式中成立的是（）

A、 $α = β$ B、 $2 α + β = 90 °$ C、 $3 α + β = 90 °$ D、 $α + 2 β = 90 °$

查看试题解析

二、填空题

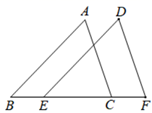
9. 在 $△ A B C$ 中， $∠ A ： ∠ B ： ∠ C = 5 ： 6 ： 7$ ，则 $△ A B C$ 是（填入“锐角三角形”、“直角三角形”或“钝角三角形”）

查看试题解析
10. 若三角形两条边的长分别是3、7，第三条边的长是整数，则第三条边长的最大值是．

查看试题解析
11. 计算： $(1 + 2 a) (1 - 2 a) (1 + 4 a^{2})$ =

查看试题解析
12. 已知 $y^{2} - 8 y + m$ 是一个完全平方式，则m的值为．

查看试题解析
13. 如图，将三角形ABC沿水平方向向右平移到三角形DEF的位置，若BF=11，EC=5，则A，D之间的距离为.

查看试题解析
14. 若 $(x + m) (x - 3) = x^{2} + n x - 12$ ，则n= ．

查看试题解析
15. 解方程 $9^{x + 1} - 3^{2 x} = 72$ ， $x =$ ．

查看试题解析
16. 对有理数 $x$ ， $y$ 定义运算： $x * y = a x + b y$ ，其中 $a$ ， $b$ 是常数．如果 $2 * (- 1) = - 4$ ， $3 * 2 > 1$ ，那么 $b$ 的取值范围是．

查看试题解析
17. 在一个三角形中，如果一个角是另一个角的3倍，这样的三角形我们称之为“灵动三角形”．例如，三个内角分别为 $120 ° ， 40 ° ， 20 °$ 的三角形是“灵动三角形”．如图 $∠ M O N = 40 °$ ，在射线 $O M$ 上找一点 $A$ ，过点 $A$ 作 $A B ⊥ O M$ 交 $O N$ 于点 $B$ ，以 $A$ 为端点作射线 $A D$ ，交线段 $O B$ 于点 $C$ （规定 $0 ° < ∠ O A C < 60 °$ ）．当 $△ A B C$ 为“灵动三角形”时， $∠ O A C$ 的度数为．

查看试题解析
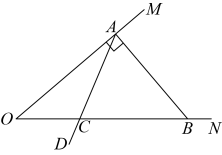18. 如图，在 $△ A B C$ 中， $B C = 6 c m$ ，射线 $A G / / B C$ ，点E从点A出发沿射线 $A G$ 以 $2 c m / s$ 的速度运动，当点E先出发 $1 s$ 后，点F也从点B出发，沿射线 $B C$ 以 $3.5 c m / s$ 的速度运动，分别连接 $A F ， C E$ .设点E运动的时间为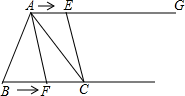 $t s$ ，其中 $t > 0$ ，当 $t =$ 时， $S_{△ A C E} = S_{△ A F C}$ .

查看试题解析

三、解答题

19. 解不等式 $\frac{2 x - 1}{4} - \frac{5 x + 2}{6} \geq - 1$

查看试题解析
20. 计算： $- 1^{2023} - | - 5 | + {(3.14 - π)}^{0} + {(- \frac{1}{3})}^{- 2}$ ．

查看试题解析
21. 已知 $10^{m} = 50$ ， $10^{n} = 0.5$ ，求：

(1)、 $m - n$ 的值；

(2)、 $9^{m} \div 3^{2 n}$ 的值

查看试题解析
22. 先化简，再求值： ${(2 x + 3 y)}^{2} - (2 x + y) (2 x - y) - 2 y (3 x + 5 y)$ ，其中 $x = - 2$ ， $y = \frac{1}{3}$ ．

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $△ A B C$ 的外角 $∠ C B D$ 的平分线BE交AC的延长线于点E，点F为AC延长线上的一点，连接DF．

(1)、若 $∠ A = 40 °$ ，求 $∠ D B E$ 的度数；

(2)、在（1）的条件下，若 $∠ F = 25 °$ ，求证： $B E ∥ D F$ ；

(3)、若 $B E ∥ D F$ ，探究 $∠ A$ 、 $∠ F$ 有怎样的数量关系，直接写出答案，不用证明．

查看试题解析
24. 填空：
$(a - b) (a + b) = a^{2} - b^{2}$ ；

$(a - b) (a^{2} + a b + b^{2}) = a^{3} - b^{3}$ ；

$(a - b) (a^{3} + a^{2} b + a b^{2} + b^{3}) = a^{4} - b^{4}$ ；

…

(1)、 $(a - b) (a^{2022} + a^{2021} b + \dots + a b^{2021} + b^{2022}) =$ ；

(2)、猜想：
$(a - b) (a^{n - 1} + a^{n - 2} b + \dots + a b^{n - 2} + b^{n - 1})$ ；（其中 $n$ 为正整数，且 $n \geq 2$ ）

(3)、利用（2）中的猜想的结论计算：
① $1 + 2 + 2^{2} + \dots + 2^{2021} + 2^{2022} + 2^{2023}$

② $3^{10} - 3^{9} + 3^{8} - 3^{7} \dots + 3^{4} - 3^{3} + 3^{2} - 3$ ．

查看试题解析
25. 如图， $∠ A O B = 40 °$ ， $O C$ 平分 $∠ A O B$ ，点D，E在射线 $O A$ ， $O C$ 上，点P是射线 $O B$ 上的一个动点，连接 $D P$ 交射线 $O C$ 于点F，设 $∠ O D P = x °$ ．

(1)、如图1，若 $D E$ $∥$ $O B$ ．
① $∠ D E O$ 的度数是 ▲ $°$ ，当 $D P ⊥ O E$ 时，x= ▲ ；
②若 $∠ E D F = ∠ E F D$ ，求x的值；

(2)、如图2，若 $D E ⊥ O A$ ，是否存在这样的x的值，使得 $∠ E F D = 4 ∠ E D F$ ？若存在，求出x的值；若不存在，说明理由．

查看试题解析
26. 完全平方公式经常可以用作适当变形来解决很多的数学问题．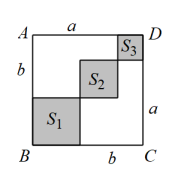

(1)、若 $x + y = 6$ ， $x^{2} + y^{2} = 30$ ，求 $x y$ 的值；

(2)、请直接写出下列问题答案：
①若 $3 a + b = 7$ ， $a b = 2$ ，则 $3 a - b =$ ；

②若 $(4 - x) (5 - x) = 8$ ，则 ${(4 - x)}^{2} + {(5 - x)}^{2} =$ ．

(3)、如图，边长为6的正方形 $A B C D$ 中放置两个长和宽分别为 $a$ ， $b (a < 6 ， b < 6)$ 的长方形，若长方形的周长为16，面积为15.75，求图中阴影部分面积 $S_{1} + S_{2} + S_{3}$ ．

查看试题解析
27. 一副三角板（ $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B A C = 30 °$ ， $△ A D E$ 中， $∠ A D E = 90 °$ ， $∠ C A D = 45 °$ ， $A C = A E$ ）按如图①方式放置，如图②将 $△ A D E$ 绕点A按逆时针方向，以每秒 $6 °$ 的速度旋转，设旋转的时间为t秒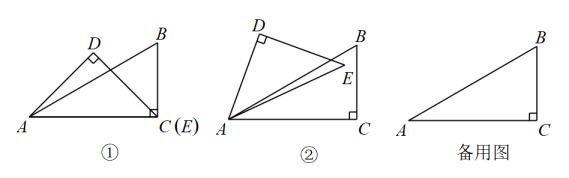（ $0 \leq t \leq 36$ ）．

(1)、图①中， $∠ B A D =$ °；

(2)、在 $△ A D E$ 绕点A旋转的过程中，当 $D E$ 与 $△ A B C$ 的一边平行时，求t的值；

(3)、在 $△ A D E$ 绕点A旋转的过程中，探究 $∠ C A E$ 与 $∠ B A D$ 之间的数量关系．

查看试题解析