江苏省连云港市灌南县2022-2023学年九年级下学期期中数学试题
试卷更新日期:2023-06-15 类型:期中考试
一、单选题
-
1. 下列四个数中,是负数的是( )A、 B、 C、 D、2. 六位同学的年龄分别是13、14、15、14、14、15岁,关于这组数据,正确说法是( )A、平均数是14 B、中位数是14.5 C、方差3 D、众数是143. 下列运算正确的是( )A、 B、 C、 D、4. 如图是某个几何体的三视图,该几何体是( ).
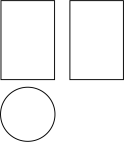 A、圆柱 B、圆锥 C、四棱柱 D、四棱锥5. 如图,已知 , 直角三角板的直角顶点在直线a上,若 , 则等于( )
A、圆柱 B、圆锥 C、四棱柱 D、四棱锥5. 如图,已知 , 直角三角板的直角顶点在直线a上,若 , 则等于( ) A、 B、 C、 D、6. 如图,A,B,C是正方形网格的格点,连接 , , 则的值是( )
A、 B、 C、 D、6. 如图,A,B,C是正方形网格的格点,连接 , , 则的值是( ) A、 B、 C、 D、7. 若函数的图象如图所示,则关于的不等式的解集为( )
A、 B、 C、 D、7. 若函数的图象如图所示,则关于的不等式的解集为( ) A、 B、 C、 D、8. 如图,在正方形中,点是边上的一点,连接 , 交与点 , 连接 , 若 , , 则正方形的边长为( )
A、 B、 C、 D、8. 如图,在正方形中,点是边上的一点,连接 , 交与点 , 连接 , 若 , , 则正方形的边长为( ) A、 B、1 C、 D、2
A、 B、1 C、 D、2二、填空题
-
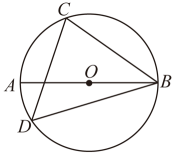
9. 二次根式 有意义的条件是.10. 已知 , ,则 .11. 华为公司自主研发的麒麟990芯片晶体管栅极宽度达0.000000007,将数据0.000000007用科学记数法表示为 .12. 用一个半径为2的半圆作一个圆锥的侧面,这个圆锥的底面圆的半径为 .13. 如图,为的直径, , 是圆周上的两点,若 , 则的度数为 .
 14. 如图.在Rt△ABC中,∠A=90°,AC=4.按以下步骤作图:(1)以点B为圆心,适当长为半径画弧,分别交线段BA,BC于点M,N;(2)以点C为圆心,BM长为半径画弧,交线段CB于点D;(3)以点D为圆心,MN长为半径画弧,与第2步中所面的弧相交于点E;(4)过点E画射线CE,与AB相交于点F.当AF=3时,BC的长是.
14. 如图.在Rt△ABC中,∠A=90°,AC=4.按以下步骤作图:(1)以点B为圆心,适当长为半径画弧,分别交线段BA,BC于点M,N;(2)以点C为圆心,BM长为半径画弧,交线段CB于点D;(3)以点D为圆心,MN长为半径画弧,与第2步中所面的弧相交于点E;(4)过点E画射线CE,与AB相交于点F.当AF=3时,BC的长是.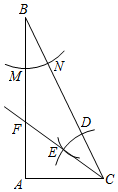 15. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是 .16. 如图,在矩形中, , , 点为边上的动点,连接 , 过点作 , 且 , 连接 , 则线段长度的最小值为 .
15. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是 .16. 如图,在矩形中, , , 点为边上的动点,连接 , 过点作 , 且 , 连接 , 则线段长度的最小值为 .
三、解答题
-
17. 计算:18. 化简:( ﹣a+1)÷ .19. 解不等式20. 为进一步开展“睡眠管理”工作,某校对部分学生的睡眠情况进行了问卷调查.设每名学生平均每天的睡眠时间为x小时,其中的分组情况是:
A组: B组:
C组: D组:E组:
根据调查结果绘制成两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
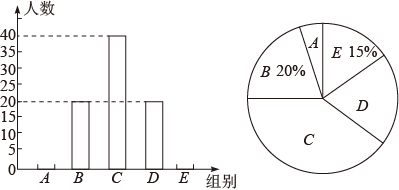 (1)、本次共调查了名学生;(2)、补全条形统计图;(3)、在扇形统计图中,求D组所对应的扇形圆心角的度数;(4)、若该校有1500名学生,请估计该校睡眠时间不足9小时的学生有多少人?21. 将图中的A型、B型、C型矩形纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.
(1)、本次共调查了名学生;(2)、补全条形统计图;(3)、在扇形统计图中,求D组所对应的扇形圆心角的度数;(4)、若该校有1500名学生,请估计该校睡眠时间不足9小时的学生有多少人?21. 将图中的A型、B型、C型矩形纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.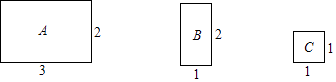 (1)、搅匀后从中摸出1个盒子,求摸出的盒子中是A型矩形纸片的概率;
(1)、搅匀后从中摸出1个盒子,求摸出的盒子中是A型矩形纸片的概率;
(2)、搅匀后先从中摸出1个盒子(不放回),再从余下的两个盒子中摸出一个盒子,求2次摸出的盒子的纸片能拼成一个新矩形的概率(不重叠无缝隙拼接).22. 某商家预测一种商品能畅销市场,就用4000元购进一批这种商品,这种商品面市后果然供不应求,商家又用8800元购进了第二批这种商品,所购数量是第一批购进数量的2倍,但单价贵了4元.该商家购进的两批商品的数量分别是多少件?23. 如图,中,点D是边上一点,点E是的中点,过点C作交的延长线于点F. (1)、求证:;(2)、若 , , 求的度数.24. 如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面30米的D处,无人机测得操控者A的俯角为30°,测得教学楼BC顶端点C处的俯角为45°.又经过人工测量测得操控者A和教学楼BC之间的距离为57米.求教学楼BC的高度.(点A,B,C,D都在同一平面上,结果保留根号)
(1)、求证:;(2)、若 , , 求的度数.24. 如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面30米的D处,无人机测得操控者A的俯角为30°,测得教学楼BC顶端点C处的俯角为45°.又经过人工测量测得操控者A和教学楼BC之间的距离为57米.求教学楼BC的高度.(点A,B,C,D都在同一平面上,结果保留根号)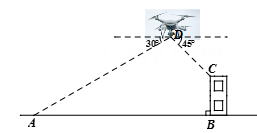 25. 如图,一次函数的图象与反比例函数的图象相交于点 , 与轴交于点,与轴交于点.
25. 如图,一次函数的图象与反比例函数的图象相交于点 , 与轴交于点,与轴交于点.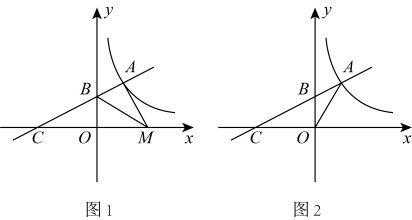 (1)、求出 , 的值;(2)、若为正轴上的一动点,当的面积为时,求的值.
(1)、求出 , 的值;(2)、若为正轴上的一动点,当的面积为时,求的值.

