江苏省连云港市灌南县2022-2023学年八年级下学期期中数学试题

试卷更新日期：2023-06-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下面四个高校校徽主体图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列调查中，适宜采用普查的是（）

A、了解一批口罩的质量情况 B、对清明节期间来秦山岛风景区游览的游客的满意度调查 C、了解我区初中生的视力情况 D、对天舟六号货运飞船的各个零部件进行检查

查看试题解析
3. 学生的心理健康问题越来越被关注，为了了解学生的心理健康状况，某中学从该校2000名学生中随机抽取500名学生进行问卷调查，下列说法正确的是（）

A、每一名学生的心理健康状况是个体 B、2000名学生是总体 C、500名学生是总体的一个样本 D、500名学生是样本容量

查看试题解析
4. 如图，将 $△ A B C$ 绕点A逆时针旋转得到△ADE，若 $∠ B = 90 °$ ， $∠ C = 50 °$ ， $∠ C A D = 10 °$ ，则旋转角的度数为（）

A、90° B、50° C、40° D、10°

查看试题解析
5. 如图，在 $▱ A B C D$ 中， $O$ 是对角线 $A C$ 与 $B D$ 的交点， $A B ⊥ A C$ ，若 $A B = 8$ ， $A C = 12$ ，则 $B D$ 的长是（）

A、20 B、22 C、24 D、26

查看试题解析
6. 如图，在四边形 $A B C D$ 中，点 $M$ 是 $A D$ 上动点，点 $N$ 是 $C D$ 上一定点，点E、 $F$ 分别是 $B M$ 、 $N M$ 的中点，当点 $M$ 从点 $A$ 向点 $D$ 移动时，下列结论一定正确的是（）

A、线段 $E F$ 的长度逐渐减小 B、线段 $E F$ 的长度逐渐增大 C、线段 $E F$ 的长度不改变 D、线段 $E F$ 的长度不能确定

查看试题解析
7. 如图，在矩形 $A B C D$ 中， $A C$ 、 $B D$ 相交于点 $O$ ， $A E$ 平分 $∠ B A D$ 交 $B C$ 于点 $E$ ．若 $∠ O D A = 30 °$ ，则 $∠ B O E$ 的度数为（）

A、 $45 °$ B、 $60 °$ C、 $65 °$ D、 $75 °$

查看试题解析
8. 如图，在 $▱ A B C D$ 中，点 $E$ 、 $F$ 分别是 $A B$ 、 $C D$ 的中点， $A F$ 与 $D E$ 交于点 $G$ ， $B F$ 与 $C E$ 交于点 $H$ ，下列说法：①四边形 $A E C F$ 是平行四边形；②四边形 $E H F G$ 是平行四边形；③当 $A B ⊥ B C$ 时，四边形 $E H F G$ 是菱形；④当 $A B = B C$ 时，四边形 $E H F G$ 是矩形，其中正确的有（）

A、①② B、①②③ C、①②④ D、①②③④

查看试题解析

二、填空题

9. 相同密度的物体，体积越大，质量越小，这是一个事件（从“随机、必然、不可能”中选一个填入）．

查看试题解析
10. 一个不透明的袋子里装有3个红球，2个黄球，1个白球，这些球除颜色外无其他差别，从袋子中随机取出一个球，取出球的可能性最大．

查看试题解析
11. 已知30个数据中的最大值为36，最小值为15，若取组距为4，则这些数据应该分的组数是．

查看试题解析
12. 在一次八年级学生身高抽查中，40个数据分别落在4个小组内，第一、二、四组数据的频率分别为0.2、0.35、0.3，则第三小组数据的频数为．

查看试题解析
13. 将五个边长都为2的正方形按如图所示摆放，点A₁、A₂、A₃、A₄分别是四个正方形的中心，则图中四块阴影部分的面积的和为．

查看试题解析
14. 如图，以正方形 $A B C D$ 的对角线 $A C$ 为一边作菱形 $A E F C$ ，点F在 $D C$ 的延长线上，连接 $A F$ 交 $B C$ 于点G，则 $∠ A G B =$ ．

查看试题解析
15. 如图，把矩形纸片 $O A B C$ 放入平面直角坐标系中，使 $O A$ 、 $O C$ 分别落在 $x$ 轴、 $y$ 轴上，连接 $A C$ ，将纸片 $O A B C$ 沿 $A C$ 折叠，使点 $B$ 落在点 $D$ 的位置， $A D$ 与 $y$ 轴交于点 $E$ ，若点 $B$ 坐标为 $(6 ， 12)$ ，则点 $E$ 的坐标为．

查看试题解析
16. 如图，在边长为 $8$ 的正方形 $A B C D$ 中，点 $G$ 是 $B C$ 边的中点， $E$ 、 $F$ 分别是 $A D$ 和 $C D$ 边上的点，则四边形 $B E F G$ 周长的最小值为．

查看试题解析

三、解答题

17. 下面是某校生物兴趣小组在相同的实验条件下，对某植物种子发芽率进行研究时所得到的数据：

试验的种子数n

500

1000

1500

2000

3000

4000

发芽的粒数m

471

946

$x$

1898

2853

3812

发芽频率 $\frac{m}{n}$

0.942

0.946

0.950

0.949

$y$

0.953

(1)、上表中的 $x =$ ， $y =$ ；

(2)、任取一粒这种植物种子，它能发芽的概率的估计值是（精确到0.01）；

(3)、若该校劳动基地需要这种植物幼苗9500棵，试估算需要准备多少粒种子进行发芽培育．

查看试题解析
18. 如图，菱形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ， $O E ⊥ A D$ ，垂足为点 $E$ ， $A C = 16$ ， $B D = 12$ ，求 $A D$ 、 $O E$ 的长．

查看试题解析
19. 2022年10月12日，“天宫课堂”第三课开讲．“太空教师”陈冬、刘洋、蔡旭哲在中国空间站为广大青少年又一次带来了精彩的太空科普课．为了激发学生的航天兴趣，某校举行了太空科普知识竞赛，竞赛结束后随机抽取了部分学生成绩进行统计，按成绩分为如下5组（满分100分），其中A组： $75 \leq x < 80$ ， B组： $80 \leq x < 85$ ， C组： $85 \leq x < 90$ ， D组： $90 \leq x < 95$ ， E组： $95 \leq x < 100$ ，并给制了如下不完整的统计图．

(1)、本次调查一共随机抽取了名学生的成绩，频数分布直方图中m=；

(2)、说明扇形统计图中B组所对应的圆心角是度，并补全频数分布直方图；

(3)、若该校共有学生1200人，则竞赛成绩小于80分的学生约有多少人？

查看试题解析
20. 如图，在平面直角坐标系中，已知 $△ A B C$ 的三个顶点的坐标分别为 $A (- 5 ， 1)$ ， $B (- 2 ， 2)$ ， $C (- 1 ， 4)$ ．

(1)、将 $△ A B C$ 绕点 $C$ 逆时针旋转 $90 °$ ，画出旋转后的 $△ A_{1} B_{1} C_{1}$ ；

(2)、画出与 $△ A B C$ 关于原点 $O$ 成中心对称的 $△ A_{2} B_{2} C_{2}$ ；

(3)、若 $D$ 点在第一象限，且以 $A$ 、 $B$ 、 $C$ 、 $D$ 为顶点的四边形是平行四边形，则 $D$ 点的坐标为．

查看试题解析
21. 如图，在 $▱ A B C D$ 中，点 $E$ 、 $F$ 在直线 $A C$ 上，且 $A E = C F$ ，求证：四边形 $D E B F$ 是平行四边形．

查看试题解析
22. 如图，在四边形 $A B C D$ 中，点P是对角线 $B D$ 的中点，点E、F分别是 $A B$ 、 $C D$ 的中点， $A D = B C$ ， $∠ P E F = 30 °$ °，求 $∠ P F E$ 的度数．

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D$ 是角平分线，过点 $C$ 作 $A D$ 的平行线，交 $△ A B C$ 外角 $∠ E A C$ 的角平分线于点 $F$ ．

(1)、判断四边形 $A D C F$ 的形状，并说明理由；

(2)、当 $△ A B C$ 满足什么条件时，四边形 $A D C F$ 是正方形？请说明理由．

查看试题解析
24. 在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交CE的延长线于点F．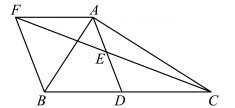

(1)、求证：四边形ADBF是菱形；

(2)、若AB＝8，菱形ADBF的面积为40，求AC的长．

查看试题解析
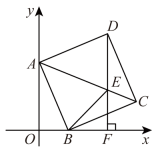25. 如图，在平面直角坐标系中，正方形 $A B C D$ 的顶点 $A$ 、 $B$ 分别在 $y$ 轴正半轴、 $x$ 轴正半轴上，过点 $D$ 作 $D F ⊥ x$ 轴交 $x$ 轴于点 $F$ ，交对角线 $A C$ 于点 $E$ ．

(1)、求证： $B E = D E$ ；

(2)、判断 $∠ E B C$ 、 $∠ F B C$ 的数量关系，并说明理由；

(3)、若点 $A$ ， $B$ 坐标分别为 $(0 ， 12)$ 、 $(5 ， 0)$ ，则 $△ B E F$ 的周长为．

查看试题解析
26. 动态几何问题是由点动、线动、形动而构成的，需要用运动与变化的眼光去观察和研究图形．有时借助特殊的四边形常常能帮助我们化“动”为“静”．

(1)、问题1：如图1，点P为矩形 $A B C D$ 对角线 $B D$ 上一动点，过点 $P$ 作 $E F ∥ B C$ ，分别交 $A B$ ， $C D$ 于点 $E$ ， $F$ ．若 $△ A E P$ 的面积为 $S_{1}$ ， $△ C F P$ 的面积为 $S_{2}$ ，则 $S_{1}$ 与 $S_{2}$ 的数量关系是 $S_{1}$ $S_{2}$ （填“>”、“<”或“=”）；

(2)、问题2：如图 $2$ ，在正方形 $A B C D$ 中， $E$ 为边 $B C$ 上一动点（不与点 $B$ 、 $C$ 重合），垂直于 $A E$ 的一条直线 $M N$ 分别交 $A B$ 、 $A E$ 、 $C D$ 于点 $M$ 、 $P$ 、 $N$ ．判断线段 $D N$ 、 $M B$ 、 $E C$ 之间的数量关系，并说明理由．

(3)、问题3：如图 $3$ ，正方形 $A B C D$ 的边长为 $4$ ， $E$ 为 $B C$ 上一点，且 $B E = 3$ ， $F$ 为 $C D$ 边上的一个动点，连接 $E F$ ，以 $E F$ 为边向左侧作等边 $△ E F G$ ，连接 $B G$ ，则 $B G$ 的最小值为．

查看试题解析

试验的种子数n	500	1000	1500	2000	3000	4000
发芽的粒数m	471	946	$x$	1898	2853	3812
发芽频率 $\frac{m}{n}$	0.942	0.946	0.950	0.949	$y$	0.953