黑龙江省齐齐哈尔市铁锋区2022-2023学年八年级下学期期中数学试卷

试卷更新日期：2023-06-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式一定是二次根式的是（）

A、 $\sqrt{- 7}$ B、 $\sqrt[3]{2 m}$ C、 $\sqrt{x^{2} + 1}$ D、 $\sqrt{\frac{b}{a}}$

查看试题解析
2. 下列各式中，运算正确的是（）

A、 $\sqrt{(- 2)^{2}}$ ＝﹣2 B、 $\sqrt{2}$ + $\sqrt{8}$ ＝ $\sqrt{10}$ C、 $\sqrt{2}$ × $\sqrt{8}$ ＝4 D、2﹣ $\sqrt{2} = \sqrt{2}$

查看试题解析
3. 下列长度的三条线段能构成直角三角形的是（）

A、2，3，4 B、1，1，2 C、4，5，6 D、8，15，17

查看试题解析
4. 下列条件不能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $A B = C D$ ， $A D = B C$ B、 $∠ A = ∠ C$ ， $∠ B = ∠ D$ C、 $A B ∥ C D$ ， $A D = B C$ D、 $A B ∥ C D$ ， $∠ B = ∠ D$

查看试题解析
5. 下列命题的逆命题成立的是（）

A、对顶角相等 B、等边三角形是锐角三角形 C、正方形的对角线互相垂直 D、平行四边形的对角线互相平分

查看试题解析
6. 已知 $1 < p < 2$ ，化简 $\sqrt{{(1 - p)}^{2}} + {(\sqrt{2 - p})}^{2} =$ （）

A、1 B、3 C、 $3 - 2 p$ D、 $1 - 2 p$

查看试题解析
7. 如图 $△ A B C$ 中， $A B = A C$ ， $B C = 6$ ， $△ D E F$ 的周长是11， $A F ⊥ B C$ 于F， $B E ⊥ A C$ 于点E，且点D是 $A B$ 的中点，则 $A F$ 的长为（）

A、36 B、 $\sqrt{55}$ C、8 D、7

查看试题解析
8. 若顺次连接四边形ABCD各边的中点所得四边形是菱形，则四边形ABCD一定是（）

A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形

查看试题解析
9. 如图，以Rt△ABC的三边为直角边分别向外作等腰直角三角形．若AB= $\sqrt{5}$ ，则图中阴影部分的面积为（）

A、 $\frac{5}{2}$ B、 $\frac{25}{4}$ C、 $\frac{25}{2}$ D、5

查看试题解析
10. 如图，正方形 $A B C D$ 的对角线 $A C$ ， $B D$ 交于点 $O$ ， $E$ 是边 $C D$ 上一点，连接 $O E$ ，过点 $O$ 作 $O F ⊥ O E$ ，交 $A D$ 于点 $F$ ．若四边形 $E O F D$ 的面积是1，则 $A B$ 的长为（）

A、1 B、 $\sqrt{2}$ C、2 D、 $2 \sqrt{2}$

查看试题解析

二、填空题

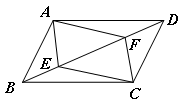
11. 若代数式 $\frac{\sqrt{3 x + 9}}{x - 2}$ 有意义，则实数x的取值范围是．

查看试题解析
12. 如图，BD是平行四边形ABCD的对角线，点E、F在BD上，要使四边形AECF是平行四边形，还需增加的一个条件是（填一种情况即可）.

查看试题解析
13. 若 $\sqrt{8 x}$ 为整数，则x的最小正整数值为．

查看试题解析
14. 如图，长方体木箱的长、宽、高分别为 $12 cm$ ， $4 cm$ ， $3 cm$ ，则能放进木箱中的直木棒最长为 $cm$ ．

查看试题解析
15. 如图，在边长为10的菱形ABCD中，对角线BD＝16，点O是线段BD上的动点，OE⊥AB于E，OF⊥AD于F.则OE+OF＝.

查看试题解析
16. 在矩形 $A B C D$ 中，点E是直线 $A D$ 上一点，若 $∠ A C B = ∠ A C E$ ， $B C = 4$ ， $D E = 1$ ，则 $C D$ 的长为．

查看试题解析
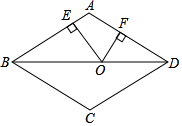17. 如图所示，已知 $△ A B C$ 是腰长为1的等腰直角三角形，以 $Rt △ A B C$ 的斜边 $A C$ 为直角边，画第2个等腰 $Rt △ A C D$ ，再以 $Rt △ A C D$ 的斜边 $A D$ 为直角边画第3个等腰 $Rt △ A D E$ ……以此类推，第2023个等腰直角三角形的斜边长为．

查看试题解析

三、解答题

18. 计算

(1)、 $\sqrt{18} - 4 \sqrt{\frac{1}{2}} + \sqrt{24} \div \sqrt{3}$ ；

(2)、 ${(2 - \sqrt{3})}^{2023} \times {(2 + \sqrt{3})}^{2022} - 2 | - \frac{\sqrt{3}}{2} | - {(- \sqrt{2})}^{0}$ ．

查看试题解析
19. 先化简，再求值： $\frac{1}{x^{2} - 1} \div (1 - \frac{x}{x + 1})$ ，其中 $x = \sqrt{2} + 1$ ．

查看试题解析
20. 已知 $a - \frac{1}{a} = 2 \sqrt{3}$ ，求 $a + \frac{1}{a}$ 的值．

查看试题解析
21. 如图，点A是网红打卡地诗博园，市民可在云龙湖边的游客观光车站B或C处乘车前往，且AB＝BC，因市政建设，点C到点A段现暂时封闭施工，为方便出行，在湖边的H处修建了一临时车站（点H在线段BC上），由H处亦可直达A处，若AC＝1km，AH＝0.8km，CH＝0.6km．

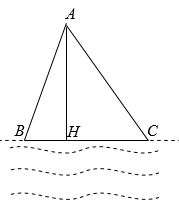(1)、判断△ACH的形状，并说明理由；

(2)、求路线AB的长．

查看试题解析
22. 如图，菱形 $A B C D$ 的对角线 $A C$ 和 $B D$ 交于点O，分别过点C、D作 $C E ∥ B D$ ， $D E ∥ A C$ ， $C E$ 和 $D E$ 交于点E．

(1)、判断四边形 $O D E C$ 的形状并说明理由；

(2)、连接 $A E$ ，交 $C D$ 于点F，当 $∠ A D B = 60 ° ， A D = 2$ 时，求 $A E$ 的长．

查看试题解析
23. 综合与实践
【课本再现】在一次课题学习活动中，老师提出了如下问题：如图1，四边形 $A B C D$ 是正方形，点E是边 $B C$ 的中点， $∠ A E F = 90 °$ ，且 $E F$ 交正方形外角平分线 $C F$ 于点F．请你探究 $A E$ 与 $E F$ 存在怎样的数量关系，并证明你的结论．

经过探究，小明得出的结论是 $A E = E F$ ．而要证明结论 $A E = E F$ ，就需要证明 $A E$ 和 $E F$ 所在的两个三角形全等，但 $△ A B E$ 和 $△ E C F$ 显然不全等（一个是直角三角形，一个是钝角三角形），考虑到点E是边 $B C$ 的中点，小明想到的方法是如图2，取 $A B$ 的中点M，连接 $E M$ ，证明 $△ A E M ≌ △ E F C$ ．从而得到 $A E = E F$ ．

(1)、小明的证法中，证明 $△ A E M$ ≌ $△ E F C$ 的条件可以为（）

A、边边边 B、边角边 C、角边角 D、斜边直角边

(2)、【类比迁移】
如图3，若把条件“点E是边 $B C$ 的中点”改为“点E是边 $B C$ 上的任意一点”，其余条件不变， $A E = E F$ 是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由．

(3)、如图4，如果点E是边 $B C$ 延长线上的任意一点，其他条件不变， $A E = E F$ 是否仍然成立？（填“是”或“否”，不需证明）；

(4)、【拓展应用】
已知：四边形 $A B C D$ 是正方形，点E是直线 $B C$ 上的一点， $∠ A E F = 90 °$ ，且 $E F$ 交正方形外角平分线 $C F$ 于点F，若 $A B = 4$ ， $C E = 2$ ，则 $E F$ 的长为．

查看试题解析
24. 综合与探究
如图，在平面直角坐标系中，点 $A 、 C$ 的坐标分别为 $(0 ， a)$ 和 $(b ， 0)$ ，且 $a ， b$ 满足 $b = \sqrt{a - 8} + \sqrt{8 - a} + 4$ ．将矩形 $O A B C$ 沿对角线 $A C$ 所在的直线折叠，点B落在点D处， $D C$ 与y轴相交于点E．

(1)、 $a =$ ， $b =$ ；

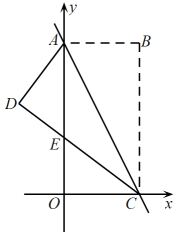(2)、试证明 $△ A D E$ ≌ $△ C O E$ ，并直接写出点E的坐标；

(3)、若点F是线段 $A C$ 上的一个动点，则 $E F + O F$ 的最小值为；

(4)、平面内是否存在点M与点N使四边形 $A C M N$ 为正方形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

查看试题解析