海南省海口市部分校2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-06-15 类型:期中考试
一、单选题
-
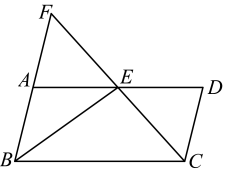
1. 要使分式有意义,则应满足的条件是( )A、 B、 C、 D、2. 约分的结果是( )A、 B、 C、 D、3. 若把分式中,x、y都扩大到原来的3倍,则分式的值( )A、不变 B、扩大3倍 C、扩大9倍 D、不确定4. 化简的结果正确的是( )A、 B、 C、 D、5. 关于x的分式方程 =1有增根,则m的值为( )A、-6 B、5 C、6 D、46. 若点P(m+3,m+1)在x轴上,则点P的坐标为( )A、(0,-2) B、(2,0) C、(4,0) D、(0,-4)7. 华为 手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为( ).A、 B、 C、 D、8. 如图,在平行四边形 中, , ,则 的度数为( )
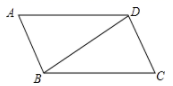 A、 B、 C、 D、9. 如图是反比例函数的图像,则一次函数的图像大致是( )
A、 B、 C、 D、9. 如图是反比例函数的图像,则一次函数的图像大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 若都在函数的图像上,则( )A、 B、 C、 D、11. 如图,反映了某产品的销售收入与销售量之间的关系,反映了该产品的销售成本与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利.根据图中信息判断该公司在赢利时的销售量为( )
10. 若都在函数的图像上,则( )A、 B、 C、 D、11. 如图,反映了某产品的销售收入与销售量之间的关系,反映了该产品的销售成本与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利.根据图中信息判断该公司在赢利时的销售量为( ) A、小于4件 B、大于4件 C、等于4件 D、不小于4件12. 如图,动点在平面直角坐标系中按图中箭头所示方向运动,第次从原点运动到点 , 第次接着运动到点 , 第次接着运动到点 , …,按这样的运动规律,经过第2023次运动后,动点的坐标是( )
A、小于4件 B、大于4件 C、等于4件 D、不小于4件12. 如图,动点在平面直角坐标系中按图中箭头所示方向运动,第次从原点运动到点 , 第次接着运动到点 , 第次接着运动到点 , …,按这样的运动规律,经过第2023次运动后,动点的坐标是( )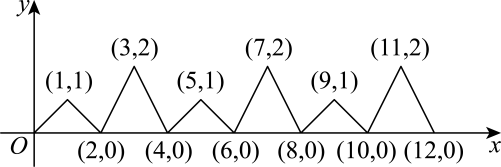 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若分式的值为0,则x= .14. 将一次函数的图像向上平移4个单位后得到的函数解析式是15. 直角坐标系中,第四象限内一点P到x轴的距离为2,到y轴的距离为5,那么点P的坐标是 .16. 一次函数的图象交轴、轴分别于点 , , 点 , 分别是 , 的中点,点C的坐标为 , 若是上一动点.当周长最小时,的坐标是 .

三、解答题
-
17. 计算题:(1)、 ;(2)、 ;(3)、 .(结果只含正整数指数幂)18. 解分式方程:(1)、 ;(2)、 .19. 甲、乙二人参加学校组织的“共读一本书活动”.已知甲每天比乙多读5页,甲读100页所用的时间与乙读80页所用的时间相等.求甲、乙每天各读书多少页?20. 如图,已知反比例函数与一次函数的图象交于点 .
 (1)、求的值;(2)、求的面积.
(1)、求的值;(2)、求的面积.