广东省中山市共进联盟2022-2023学年八年级下学期期中数学试题

试卷更新日期：2023-06-15 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $\sqrt{{(- 2)}^{2}}$ 的结果为（）

A、2 B、-2 C、4 D、 $\pm 2$

查看试题解析
2. 以下四组数中，是勾股数的是（）

A、1，2，3 B、12，13，4 C、8，15，17 D、4，5，6

查看试题解析
3. 如图，平行四边形 $A B C D$ 中，已知 $A B = 6$ ，则 $C D$ 的值是（）

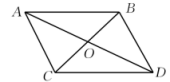A、8 B、12 C、6 D、 $4 \sqrt{3}$

查看试题解析
4. 下列曲线中，不能表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
5. 下列选项中，最简二次根式是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{8}$ C、 $\sqrt{15}$ D、 $\sqrt{20}$

查看试题解析
6. 下列说法不正确的是（）

A、一组对边平行且相等的四边形是平行四边形 B、平行四边形的对角相等，邻角互补 C、对角线互相平分的四边形是平行四边形 D、两组对角互补的四边形是平行四边形

查看试题解析
7. 如图，菱形 $A B C D$ 的对角线 $A C ， B D$ 相交于点O，点E在 $O B$ 上，连接 $A E$ ，点F为 $C D$ 的中点，连接 $O F$ ，若 $A E = B E$ ， $O E = 3$ ， $O A = 4$ ，则线段 $O F$ 的长为（）

A、5 B、 $2 \sqrt{5}$ C、 $3 \sqrt{3}$ D、6

查看试题解析
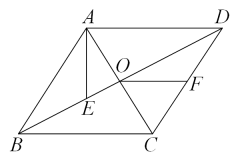8. 为了方便体温监测，某学校在大门入口的正上方 $A$ 处装有红外线激光测温仪（如图所示），测温仪离地面的距离 $A B = 2.2$ 米，当人体进入感应范围内时，测温仪就会自动测温并报告人体体温．当身高为1.7米的小明 $C D$ 正对门缓慢走到离门1.2米处时（即 $B C = 1.2$ 米），测温仪自动显示体温，此时小明头顶到测温仪的距离 $A D$ 等于（）

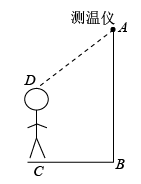A、0.5米 B、1.2米 C、1.3米 D、1.7米

查看试题解析
9. 如图，数轴上点A表示的实数是（）

A、 $\sqrt{5} - 1$ B、 $\sqrt{5} + 1$ C、 $\sqrt{3} + 1$ D、 $\sqrt{3} - 1$

查看试题解析
10. 如图，矩形 $A B C D$ 中，点 $M$ 、 $N$ 分别为边 $A D$ 、 $B C$ 上两动点，且 $A B = 8$ ， $B C = 10$ ，沿 $M N$ 翻折矩形，使得 $D$ 点恰好落在边 $A B$ （含端点）上，记作点 $G$ ，翻折后点 $C$ 对应点 $H$ ，则 $N H$ 的最小值为（）

A、 $\frac{3}{2}$ B、 $\sqrt{3}$ C、 $\frac{9}{5}$ D、2

查看试题解析

二、填空题

11. 若式子 $\sqrt{x + 6}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 如图，供给船要给C岛运送物资，从海岸线AB的港口A出发向北偏东40°方向直线航行60nmile到达C岛．测得海岸线上的港口B在C岛南偏东50°方向．若A，B两港口之间的距离为65nmile，则C岛到港口B的距离是nmile．

查看试题解析
13. 一个等腰三角形的周长为24，其中它的腰长 $x$ 为自变量，底边长 $y$ 为因变量，则用 $x$ 表示 $y$ 的关系式是.

查看试题解析
14. 在平面直角坐标系中，已知 $A (0 ， 0)$ ， $B (4 ， 0)$ ， $C (3 ， 3)$ ，若以A、B、C、D为顶点的四边形是平行四边形，则D的坐标为．

查看试题解析
15. 如图，正方形 $A B C D$ 的边长为1，以 $A C$ 为边作第二个正方形 $A C E F$ ，再以 $C F$ 为边作第三个正方形 $F C G H$ …，按照这样规律作下去，第10个正方形的边长为．

查看试题解析

三、解答题

16. 化简： $\sqrt{48} \div \sqrt{3} - 2 \sqrt{\frac{1}{5}} \times \sqrt{10} + 2 \sqrt{2}$ ．

查看试题解析
17. 如图，在四边形 $A B C D$ 中， $∠ B = 90 °$ ， $∠ B C A = 60 °$ ， $A C = 2 \sqrt{2}$ ， $D A = 1$ ， $C D = 3$ ．求四边形 $A B C D$ 的面积．

查看试题解析
18. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90^{\circ}$ ，点D是斜边 $A B$ 的中点， $C E ∥ A B$ ， $C D ∥ B E$ ．
求证：四边形CDBE是菱形．

查看试题解析
19. 小红星期天从家里出发骑车去舅舅家做客，当她骑了一段路时，想起要买个礼物送给表弟，于是又折回到刚经过的一家商店，买好礼物后又继续骑车去舅舅家，如图是她本次去舅舅家所用的时间与小红离家的距离的关系式示意图．根据图中提供的信息回答下列问题：

(1)、小红家到舅舅家的路程是米，小红在商店停留了分钟；

(2)、在整个去舅舅家的途中哪个时间段小红骑车速度最快？最快的速度是多少米/分？

(3)、本次去舅舅家的行程中，小红一共行驶了多少米？

查看试题解析
20. 在数学学习活动中，小华和他的同学遇到一道题：已知 $a = \frac{1}{2 + \sqrt{3}}$ ，求 $a + 1$ 的值．
小华是这样解答的： $∵ a = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3} ∴ a + 1 = 3 - \sqrt{3}$ ，请你根据小华的解题过程，解决下列问题．

(1)、填空： $\frac{1}{\sqrt{3} - \sqrt{2}} =$ ； $\frac{1}{\sqrt{3} - 1} =$ ；

(2)、化简： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{289} + \sqrt{288}}$ ．

查看试题解析
21. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点 $D ， E ， F$ 分别是 $A C ， A B$ 的中点，O是 $D F$ 的中点， $E O$ 的延长线交线段 $B D$ 于点G，连结 $D E ， E F ， F G$ ．

(1)、求证：四边形 $D E F G$ 是平行四边形．

(2)、当 $A D ＝ 5 ， D C = 2$ 时，求 $F G$ 的长．

查看试题解析
22. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $B C > A C$ ， $C D ⊥ A B$ 于点 $D$ ，点 $E$ 是 $A B$ 的中点，连接 $C E$ ．

(1)、若 $A C = 3$ ， $B C = 4$ ，求 $C D$ 的长；

(2)、求证： $B D^{2} - A D^{2} = 2 D E \cdot A B$ ．

查看试题解析
23. 如图所示，AD $/ /$ BC，∠BAD＝90°，以B为圆心，BC长为半径画弧，与射线AD相交于点E，连接BE，过C作CF⊥BE于点F．

(1)、线段BF与图中哪条线段相等？写出来并加以证明：

(2)、若AB＝8，BC＝10，P从E沿直线ED方向运动，Q从C出发沿直线CB方向运动，两点同时出发且速度均为每秒1个单位．
①求出当t为何值时，四边形EPCQ是矩形；

②求出当t为何值时，四边形EPCQ是菱形．

查看试题解析