广东省惠州市惠东县第五片区2022-2023学年八年级下学期期中考试数学试题

试卷更新日期：2023-06-15 类型：期中考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{a + 1}$ 在实数范围内有意义，则a的取值范围是（）

A、 $a \geq 1$ B、 $a \geq - 1$ C、 $a > 1$ D、 $a \leq - 1$

查看试题解析
2. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{8}$ C、 $\sqrt{\frac{1}{3}}$ D、 $\sqrt{4}$

查看试题解析
3. 以下列各组数据为边长作三角形，其中不能组成直角三角形的是（）

A、4，6，8 B、5，12，13 C、6，8，10 D、7，24，25

查看试题解析
4. 如图，在 $▱ A B C D$ 中， $∠ B + ∠ D = 100 °$ ，则 $∠ A$ 的度数是（）

A、 $50 °$ B、 $65 °$ C、 $100 °$ D、 $130 °$

查看试题解析
5. 下列运算正确的是（）

A、 $2 \sqrt{2} + 3 \sqrt{3} = 5 \sqrt{5}$ B、 $\sqrt{20} \div \sqrt{5} = 4$ C、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$ D、 $\sqrt{4 \frac{1}{16}} = 2 \frac{1}{4}$

查看试题解析
6. 如图，在菱形ABCD中，O、F分别是AC、BC的中点，若OF＝3，则AD的长为（）

A、3 B、6 C、9 D、12

查看试题解析
7. 如图，已知四边形 $A B C D$ ，对角线 $A C$ 和 $B D$ 相交于O，下面选项不能得出四边形 $A B C D$ 是平行四边形的是（）

A、 $A B = C D$ ， $A D = B C$ B、 $A B ∥ C D$ ，且 $A B = C D$ C、 $A B ∥ C D$ ，且 $A D = B C$ D、 $A O = C O$ ， $B O = D O$

查看试题解析
8. 如图，数轴上点A表示的实数是（）

A、 $\sqrt{5} - 1$ B、 $\sqrt{5} + 1$ C、 $\sqrt{3} + 1$ D、 $\sqrt{3} - 1$

查看试题解析
9. 如图，矩形ABCD中，AB=2，E是AC的中点，∠AED=120°，则AD长为（）

A、 $2 \sqrt{3}$ B、4 C、 $3 \sqrt{2}$ D、5

查看试题解析
10. 如图，已知菱形ABCD的两条对角线分别为6和8，M、N分别是边BC、CD的中点，P是对角线BD上一点，则PM+PN的最小值是（　　）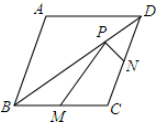

A、5 B、10 C、6 D、8

查看试题解析

二、填空题

11. 化简 $\sqrt{{(- 5)}^{2}}$ 的结果是．

查看试题解析
12. 在平面直角坐标系中，点P(-1，2)到原点的距离是

查看试题解析
13. 如图，在平行四边形 $A B C D$ 中， $A D = 10$ ，对角线 $A C$ 与 $B D$ 相交于点O， $A C + B D = 22$ ，则 $△ B O C$ 的周长为．

查看试题解析
14. 如图，在菱形ABCD中，AB=10，AC=12，则它的面积是 .

查看试题解析
15. 如图，已知正方形 $A B C D$ 的边长为4，P是对角线 $B D$ 上一点， $P E ⊥ B C$ 于点E， $P F ⊥ C D$ 于点F，连接 $A P$ ， $E F$ ．给出下列结论：① $P D = \sqrt{2} D F$ ；②四边形 $P E C F$ 的周长为8；③ $E F$ 的最小值为2；④ $A P ⊥ E F$ ．其中正确结论的序号为．

查看试题解析

三、解答题

16. 计算： $\sqrt{75} + \sqrt{8} - \sqrt{18} - \sqrt{6} \times \sqrt{2}$

查看试题解析
17. 如图， $▱ A B C D$ 的对角线 $A C$ 和 $B D$ 交于点O，E、F分别是 $O A$ 、 $O C$ 上的点且 $A E = C F$ ．求证： $B E = D F$ ．

查看试题解析
18. 如图，小明爸爸在鱼池边开了一块四边形土地种了一些蔬菜，爸爸让小明计算这块土地的面积，以便估算产量．小明测得 $A B = 3 m ， A D = 4 m ， C D = 12 m ， B C = 13 m$ ，又已知 $∠ A = 90 °$ ．求这块土地的面积．

查看试题解析
19. 已知 $x = 1 - \sqrt{2}$ ， $y = 1 + \sqrt{2}$ ．

(1)、求 $x^{2} + 3 x y + y^{2}$ 的值；

(2)、求 $\frac{y}{x} - \frac{x}{y}$ 的值

查看试题解析
20. 如图，△ABC中，AB=AC=4，D、E分别为AB、AC的中点，连接CD，过E作EF $∥$ DC交BC的延长线于F；

(1)、求证：DE=CF；

(2)、若∠B=60°，求EF的长.

查看试题解析
21. 如图，在矩形 $A B C D$ 中， $O$ 是对角线 $A C$ 的中点，过点 $O$ 作直线分别与矩形的边 $A D$ ， $B C$ 交于 $M$ ， $N$ 两点，连接 $C M$ ， $A N$ ．

(1)、求证：四边形 $A N C M$ 为平行四边形；

(2)、若 $M N ⊥ A C$ 且 $A D = 6$ ， $A B = 2$ ，求 $D M$ 的长．

查看试题解析
22. 阅读材料：
（一）在进行二次根式的化简与运算时，我们有时还会碰上如 $\frac{2}{\sqrt{3} + 1}$ 一样的式子，其实我们还可以将其进一步化简：

$\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 \times (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \sqrt{3} - 1$ ．

那么我们称这个过程为分式的分母有理化．

（二）如果我们能找到两个实数 $x$ ， $y$ 使 $x + y = a$ 且 $x y = b$ ，

这样 $\sqrt{a + 2 \sqrt{b}} = \sqrt{{(\sqrt{x})}^{2} + {(\sqrt{y})}^{2} + 2 \sqrt{x} \cdot \sqrt{y}} = \sqrt{{(\sqrt{x} + \sqrt{y})}^{2}} = \sqrt{x} + \sqrt{y}$ ，那么我们就称 $\sqrt{a + 2 \sqrt{b}}$ 为“和谐二次根式”，则上述过程就称之为化简“和谐二次根式．”

例如： $\sqrt{3 + 2 \sqrt{2}} = \sqrt{{(\sqrt{1})}^{2} + {(\sqrt{2})}^{2} + 2 \sqrt{1} \cdot \sqrt{2}} = \sqrt{{(1 + \sqrt{2})}^{2}} = 1 + \sqrt{2}$ ．

根据阅读材料解决下列问题：

(1)、化简： $\frac{2}{\sqrt{3} - 1}$ ；

(2)、化简“和谐二次根式”
① $\sqrt{4 + 2 \sqrt{3}} =$ ；② $\sqrt{6 - 2 \sqrt{5}} =$ ．

(3)、已知 $m = \frac{1}{\sqrt{5 + 2 \sqrt{6}}}$ ， $n = \frac{1}{\sqrt{5 - 2 \sqrt{6}}}$ ，求 $\frac{m - n}{m + n}$ 的值．

查看试题解析
23. 如图，已知四边形 $A B C D$ 是正方形， $A B = 2 \sqrt{2}$ ，点E为对角线 $A C$ 上一动点，连接 $D E$ ．过点E作 $E F ⊥ D E$ ，交射线 $B C$ 点F，以 $D E 、 E F$ 为邻边作矩形 $D E F G$ ．连接 $C G$ ．

(1)、连接 $B E$ ，求证： $B E = D E$ ．

(2)、求证：矩形 $D E F G$ 是正方形．

(3)、探究： $C E + C G$ 的值是否为定值？若是，请求出这个定值，若不是，请说明理由．

查看试题解析