浙江省丽水市2023年中考数学试卷

试卷更新日期：2023-06-15 类型：中考真卷

进入 出卷网 下载

一、选择题(本题有10小题，每小题3分，共30分)

  • 1. 实数-3的相反数是（    )
    A、−13 B、13 C、3 D、-3

    查看试题解析

  • 2. 计算a2+2a2的正确结果是（ ）
    A、2a2 B、2a4 C、3a2 D、3a4

    查看试题解析

  • 3. 某校准备组织红色研学活动，需要从梅岐、王村口、住龙、小顺四个红色教育基地中任选一个前往研学，选中梅岐红色教育基地的概率是（ ）
    A、12 B、14 C、13 D、34

    查看试题解析

  • 4. 如图，箭头所指的是某陶艺工作室用于垫放陶器的5块相同的耐火砖搭成的几何体，它的主视图是（ ）

    A、 B、 C、 D、

    查看试题解析

  • 5. 在平面直角坐标系中，点P(-1，m2+1)位于（ ）
    A、第一象限 B、第二象限 C、第三象限 D、第四象限

    查看试题解析

  • 6. 小霞原有存款52元，小明原有存款70元从这个月开始，小霞每月存15元零花钱，小明每月存12元零花钱，设经过n个月后小霞的存款超过小明，可列不等式为（ ）
    A、52+15n>70+12n B、52+15n<70+12n C、52+12n>70+15n D、52+12n<70+15n

    查看试题解析

  • 7. 如图，在菱形ABCD中，AB=1，∠DAB=60°，则AC的长为（ ）

    A、12 B、1 C、32 D、3

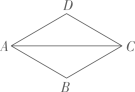    查看试题解析

  • 8. 如果100N的压力F作用于物体上，产生的压强p要大于1000Pa，则下列关于物体受力面积S(m2)的说法正确的是（ ）
    A、S小于0.1m2 B、S大于0.1m2 C、S小于10m2 D、S大于10m2

    查看试题解析

  • 9. 一个球从地面竖直向上弹起时的速度为10米/秒，经过t(秒)时球距离地面的高度h(米)适用公式h=10t-5t2 ， 那么球弹起后又回到地面所花的时间t(秒)是（ ）
    A、5 B、10 C、1 D、2

    查看试题解析

  • 10. 如图，在四边形ABCD中，AD∥BC，∠C=45°，以AB为腰作等腰直角三角形BAE，顶点E恰好落在CD边上，若AD=1．则CE的长是（    ）

    A、2 B、22 C、2 D、1

    查看试题解析

二、填空题(本题有6小题，每小題4分，共24分)

  • 11. 分解因式：x2-9= ，

    查看试题解析

  • 12. 青田县“稻鱼共生”种养方式因稻鱼双收、互惠共生而受到农户青睐，现有一农户在5块面积相等的稻田里养殖田鱼，产量分别是(单位：kg)：12，13，15，17，18．则这5块稻田的田鱼平均产量是kg．

    查看试题解析

  • 13. 如图，在△ABC中，AC的垂直平分线交BC于点D，交AC于点E，∠B=∠ADB．若AB=4，则DC的长是。

    查看试题解析

  • 14. 小慧同学在学习了九年级上册“4.1比例线段”3节课后，发现学习内容是一个逐步特殊化的过程，请在横线上填写适当的数值+感受这种特殊化的学习过程．

    查看试题解析

  • 15. 古代中国的数学专著《九章算术》中有一题：“今有生丝三十斤，千之，耗三斤十二两．今有干丝一十二斤，问生丝几何？“意思是：“今有生丝30斤，干燥后耗损3斤12两(古代中国1斤等于16两)．今有干丝12斤，问原有生丝多少？”则原有生丝为斤．

    查看试题解析

  • 16. 如图，分别以a，b，m，n为边长作正方形，已知m>n且满足am-bn=2．an+bm=4．

    (1)、若a=3，b=4，则图1阴影部分的面积是；
    (2)、若图1阴影部分的面积为3．图2四边形ABCD的面积为5，则图2阴影部分的面积是 。

    查看试题解析

三、解答题(本题有8小题，第17-19题每题6分，第20，21题每题8分．第22、23题每题10分，第24题12分，共66分，各小题部必须写出解答过程)

  • 17. 计算：|−12|+（-2023）0+2-1

    查看试题解析

  • 18. 解一元一次不等式组：{x+2>3 ， 2x−1<5

    查看试题解析

  • 19. 如图，某工厂为了提升生产过程中所产生废气的净化效率，需在气体净化设备上增加一条管道A-D-C．已知DC⊥BC，AB⊥BC．∠A=60°，AB=11m，CD=4m．求管道A-D-C的总长.

    查看试题解析

  • 20. 为全面提升中小学生体质健康水平，我市开展了儿童青少年“正脊行动”。人民医院专家组随机抽取某校各年级部分学生进行了脊柱健康状况筛查．根据筛查情况，李老师绘制了两幅不完整的统计图表，请根据图表信息解答下列问题：

    抽取的学生脊柱健康情况统计表

    类别

    检查结果

    人数

    A

    正常

    170

    B

    轻度侧弯

    		  

    C

    中度侧弯

    7

    D

    重度侧弯

    		  

    (1)、求所抽取的学生总人数；
    (2)、该校共有学生1600人，请估算脊柱侧弯程度为中度和重度的总人数；
    (3)、为保护学生脊柱健康，请结合上述统计数据，提出一条合理的建议.

    查看试题解析

  • 21. 我市“共富工坊"问梅借力，某公司产品销售量得到大幅提升．为促进生产，公司提供了两种付给员工月报酬的方案，如图所示，员工可以任选一种方案与公司签订合同，看图解答下列问题：

    (1)、直接写出员工生产多少件产品时，两种方案付给的报酬一样多；
    (2)、求方案二y关于x的函数表达式；
    (3)、如果你是劳务服务部门的工作人员，你如何指导员工根据自己的生产能力选择方案.

    查看试题解析

  • 22. 某数学兴趣小组活动，准备将一张三角形纸片(如图)进行如下操作．并进行猜想和证明。

    (1)、用三角板分别取AB，AC的中点D，E，连结DE，画AF⊥DE于点F；
    (2)、用(1)中所画的三块图形经过旋转或平移拼出一个四边形(无继隙无重叠)．并用三角板画出示意图：
    (3)、请判断(2)中所拼的四边形的形状，并说明理由

    查看试题解析

  • 23. 已知点(-m，0)和(3m，0)在二次函数y=ax2+bx+3(a，b是常数，a≠0)的图象上。
    (1)、当m=-1时，求a和b的值：
    (2)、若二次函数的图象经过点A(n，3)且点A不在坐标轴上，当-2<m<-1时，求n的取值范围：
    (3)、求证：b2+4a=0．

    查看试题解析

  • 24. 如图，在⊙O中，AB是一条不过圆心O的弦，点C，D是AB⌢的三等分点，直径CE交AB于点F，连结AD交CF于点G，连结AC，过点C的切线交BA的延长线于点H．

     

    (1)、求证：AD∥HC；
    (2)、若OGGC=2，求tan∠FAG的值；
    (3)、连结BC交AD于点N．若⊙O的半径为5．

    下面三个问题，依次按照易、中、难排列，对应的分值为2分、3分、4分，请根据自己的认知水平，选择其中一道问题进行解答。

    ①若OF=52 ， 求BC的长；

    ②若AH=10 ， 求△ANB的局长：

    ③若HF·AB=88．求△BHC的面积.

    查看试题解析