广东省广州市增城区2022-2023学年七年级下学期数学期中测试题

试卷更新日期：2023-06-15 类型：期中考试

进入出卷网下载

一、选择题

1. 2022年，中国举办了第二十四届冬季奥林匹克运动会，如图，通过平移右图吉祥物“冰墩墩”可以得到的图形是（）

A、 B、 C、 D、

查看试题解析
2. 如图，直线a，b相交于点O，若 $∠ 1 + ∠ 2 = 90 °$ ，则 $∠ 3$ 等于（）

A、 $120 °$ B、 $125 °$ C、 $130 °$ D、 $135 °$

查看试题解析
3. 下列实数 $- 2$ 、0、 $\sqrt{9}$ ， $π$ 中，无理数是（）

A、-2 B、0 C、 $\sqrt{9}$ D、 $π$

查看试题解析
4. 如图，直线 $a ∥ b$ ，直线 $A B ⊥ A C$ ，若 $∠ 1 = 50 °$ ，则 $∠ 2 =$ （）

A、 $30 °$ B、 $40 °$ C、 $45 °$ D、 $50 °$

查看试题解析
5. 下列说法中，错误的是（）

A、4的算术平方根是±2 B、 $\sqrt{81}$ 的平方根是±3 C、8的立方根是2 D、立方根等于－1的实数是－1

查看试题解析
6. 若xy＞0，则关于点P（x，y）的说法正确的是（）

A、在一或二象限 B、在一或四象限 C、在二或四象限 D、在一或三象限

查看试题解析
7. 如图，要使AD∥BC，则需要添加的条件是（）

A、∠A=∠CBE B、∠A=∠C C、∠C=∠CBE D、∠A+∠D=180°

查看试题解析
8. 广州，美丽的羊城，没有冬季严寒，是热门旅游城市之一，经济发达，历史人文底蕴深厚．下列表示广州市地理位置最合理的是（）

A、在中国南部 B、毗邻港滨 C、距离北京2000公里 D、东经 $113 °$ 、北纬 $23 °$

查看试题解析
9. 如图，∠1＝70°，直线a平移后得到直线b，则∠2－∠3（）

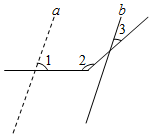A、70° B、180° C、110° D、80°

查看试题解析
10. 如图所示，在平面直角坐标系中，半经均为1个单位长度的半圆 $O_{1} ， O_{2} ， O_{3} ， \dots$ ，组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒 $\frac{π}{2}$ 个单位长度，则第2023秒时，点P的坐标是（）

A、 $(2023 ， - 1)$ B、 $(2023 ， 0)$ C、 $(2023 ， 2)$ D、 $(2023 ， 1)$

查看试题解析

二、填空题

11. 比较大小： $\sqrt{37}$ 6， $\frac{\sqrt{5} - 1}{2}$ $\frac{1}{2}$ ．（用“ $>$ ”“ $<$ ”连接）

查看试题解析
12. 将含30°角的三角板如图摆放，AB $∥$ CD，若 $∠ 1$ ＝20°，则 $∠ 2$ 的度数是.

查看试题解析
13. 如图，在正方形的网格中建立平面直角坐标系，若B、C两点的坐标分别是 $B (0 ， 2)$ ， $C (1 ， 0)$ ，则A点的坐标为．

查看试题解析
14. 把命题“任意两个直角都相等”改写成“如果…………，那么…………”的形式是．

查看试题解析
15. 已知 $\sqrt{3.12} \approx$ 1.766， $\sqrt{31.2} \approx$ 5.586，则 $\sqrt{3120} \approx$ .

查看试题解析
16. 在平面直角坐标系中，四边形ABCD四个顶点分别是A（−4，−4），B（1，−4），C（1，−2），D（−4，−2）．设点M是四边形ABCD边上的动点，直线AM将四边形ABCD的周长分为3：4两部分，则点M的坐标是．

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{9} + \sqrt[3]{- 8} + {(- 2)}^{2}$

(2)、 $\sqrt[3]{27} + {(- 1)}^{2023} + | - \sqrt{3} | - \sqrt{16}$

查看试题解析
18. 解方程：

(1)、 $25 x^{2} - 36 = 0$

(2)、 $2 {(x + 1)}^{3} = - 16$

查看试题解析
19. 按要求画图及填空：在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系，原点O及 $△ A B C$ 的顶点都在格点上．

(1)、点A的坐标为．

(2)、将 $△ A B C$ 先向下平移2个单位长度，再向右平移5个单位长度得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ． $△ A B C$ 内一点 $P (x_{0} ， y_{0})$ ，平移后P的对应点 $P_{1}$ 坐标为．

(3)、 $△ A_{1} B_{1} C_{1}$ 的面积为．

查看试题解析
20. 把下面的说理过程补充完整：
如图，已知： $∠ 1 + ∠ 2 = 180 °$ ， $∠ 3 = ∠ B$ ，试判断 $∠ A E D$ 与 $∠ C$ 的关系，并说明理由．
解： $∠ A E D = ∠ C$ ．
理由∵ $∠ 1 = ∠ A D F$ （      ）， $∠ 1 + ∠ 2 = 180 °$ （已知）
∴ $∠ 2 + ∠ A D F = 180 °$ （等量代换）
∴ $E F ∥ A B$ （      ）
∴ $∠ 3 = ∠ A D E$ （      ）
∵ $∠ 3 = ∠ B$ （已知）
∴ $∠ B = ∠ A D E$ （等量代换），
∴ $D E ∥ B C$ （同位角相等，两直线平行）
∴ $∠ A E D = ∠ C$ （      ）．

查看试题解析
21. 已知某正数x的两个平方根分别是 $a - 3$ 和 $2 a + 15$ ， y的立方根是-3． $z$ 是 $\sqrt{13}$ 的整数部分．求 $x + y - 2 z$ 的平方根．

查看试题解析
22. 如图所示，直线AB，CD相交于点O， $∠ B O D = ∠ B O E$ ， OF平分 $∠ C O E$ ．

(1)、判断OF与OB的位置关系，并说明理由．

(2)、 $∠ A O C ： ∠ A O D = 1 ： 5$ ，求 $∠ E O F$ 的度数．

查看试题解析
23. 已知点 $P (2 a - 2 ， a + 5)$ ，解答下列各题：

(1)、点 $P$ 在 $x$ 轴上，求出点 $P$ 的坐标；

(2)、点 $Q$ 的坐标为 $(4 ， 5)$ ，直线 $P Q ∥ y$ 轴，求出点 $P$ 的坐标；

(3)、若点 $P$ 在第二象限，且它到 $x$ 轴的距离与 $y$ 轴的距离相等，求 $a^{2023} + 2023$ 的值.

查看试题解析
24. 如图，在平面直为坐标系中，点A，B的坐标分别为 $A (0 ， a)$ ， $B (b ， a)$ ，且a、b满足 ${(a - 2)}^{2} + | b - 4 | = 0$ ，现同时将点A，B分别向下平移2个单位，再向左平移1个单位，分别得到点A，B的对应点C，D，连接 $A C$ ， $B D$ ， $A B$ ．

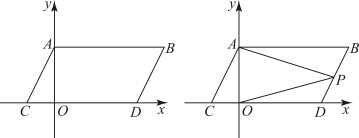(1)、求点C，D的坐标及四边形 $A C D B$ 的面积 $S_{四边形 A C D B}$ ；

(2)、在y轴上是否存在一点M，连接 $M C$ ， $M A$ ，使 $S_{△ M C A} = \frac{1}{2} S_{四边形 A C D B}$ ？若存在这样一点，求出点M的坐标，若不存在，试说明理由；

(3)、点P是直线 $B D$ 上的一个动点，连接 $P A$ ， $P O$ ，当点P在直线 $B D$ 上移动时（不与B，D重合），直接写出 $∠ B A P$ ， $∠ D O P$ ， $∠ A P O$ 之间满足的数量关系．

查看试题解析