2022-2023学年浙教版数学八年级下册6.3反比例函数的应用课后测验

试卷更新日期：2023-06-14 类型：同步测试

进入出卷网下载

一、单选题

1. 密闭容器内有一定质量的二氧化碳，当容器的体积V（单位： $m^{3}$ ）变化时，气体的密度ρ（单位： $k g / m^{3}$ ）随之变化．已知密度ρ与体积V是反比例函数关系，它的图像如图所示，当 $V = 5 m^{3}$ 时， $ρ = 1.98 k g / m^{3}$ ．根据图像可知，下列说法不正确的是（）

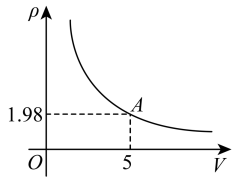A、ρ与V的函数关系式是 $ρ = \frac{9.9}{V} (V > 0)$ B、当 $ρ = 9$ 时， $V = 1.1$ C、当 $V > 5$ 时， $ρ > 1.98$ D、当 $3 < V < 9$ 时，ρ的变化范围是 $1.1 < ρ < 3.3$

查看试题解析
2. 如图1是一个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流 $I (A)$ 与电阻 $R (Ω)$ 成反比例函数的图象，该图象经过点 $P (880 ， 0.25)$ .根据图象可知，下列说法正确的是（）

A、当 $R < 0.25$ 时， $I < 880$ B、I与R的函数关系式是 $I = \frac{200}{R} (R > 0)$ C、当 $R > 1000$ 时， $I > 0.22$ D、当 $880 < R < 1000$ 时，I的取值范围是 $0.22 < I < 0.25$

查看试题解析
3. 某市举行中学生数学知识竞赛，如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况，.其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上，则这四所学校在这次数学知识竞赛中成绩优秀人数最多的是（）.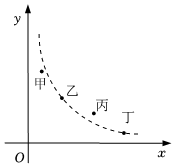

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 初三年级甲、乙、丙、丁四个级部举行了知识竞赛，如图，平面直角坐标系中，x轴表示级部参赛人数，y轴表示竞赛成绩的优秀率（该级部优秀人数与该级部参加竞赛人数的比值），其中描述甲、丁两个级部情况的点恰好在同一个反比例函数的图象上，则这四个级部在这次知识竞赛中成绩优秀人数的多少正确的是（）

A、甲 $>$ 乙 $>$ 丙 $>$ 丁 B、丙 $>$ 甲 $=$ 丁 $>$ 乙 C、甲 $=$ 丁 $>$ 乙 $>$ 丙 D、乙 $>$ 甲 $=$ 丁 $>$ 丙

查看试题解析
5. 某个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现．如图所示的是该台灯的电流 $I (A)$ 与电阻 $R (Ω)$ 的关系图象，该图象经过点 $P (880 ， 0.25)$ ．根据图象可知，下列说法正确的是（）

A、当 $I < 0.25$ 时， $R < 880$ B、I与R的函数关系式是 $I = \frac{200}{R} (R > 0)$ C、当 $R > 1000$ 时， $I > 0.22$ D、当 $880 < R < 1000$ 时，I的取值范围是 $0.22 < I < 0.25$

查看试题解析
6. 公元前3世纪，古希腊科学家阿基米德发现了“杠杆原理”：杠杆平衡时，阻力×阻力臂=动力×动力臂，当用撬棍撬动一块石头时，发现阻力和阻力臂分别为 $1200 N$ 和 $0.5 m$ ，关于动力F和动力臂l，下列说法错误的是（）

A、F与l的积为定值 B、F随l的增大而减小 C、当l为 $1.5 m$ 时，撬动石头至少需要 $400 N$ 的力 D、F关于l的函数图象位于第一、第三象限

查看试题解析
7. 某闭合并联电路中，各支路电流 $I (A)$ 与电阻 $R (Ω)$ 成反比例，如图表示该电路I与电阻R的函数关系图象，若该电路中某导体电阻为 $4 Ω$ ，则导体内通过的电流为(　　)

A、 $2 A$ B、 $2.5 A$ C、 $5 A$ D、 $10 A$

查看试题解析
8. 如图是4个台阶的示意图，每个台阶的高和宽分别是1和2，每个台阶凸出的角的顶点记作T_m（m为1～4的整数），函数y＝ $\frac{k}{x}$ （x＞0）的图象为曲线L．若曲线L使得T₁～T₄ ，这些点分布在它的两侧，每侧各2个点，则k的取值范围是（）

A、8≤k≤12 B、8≤k＜12 C、8＜k≤12 D、8＜k＜12

查看试题解析
9. 在同一平面直角坐标系中，一次函数 $y_{1} = k_{1} x + b$ 与反比例函数 $y_{2} = \frac{k_{2}}{x} (x > 0)$ 的图像如图所示、则当 $y_{1} > y_{2}$ 时，自变量 $x$ 的取值范围为（）

A、 $x < 1$ B、 $x > 3$ C、 $0 < x < 1$ D、 $1 < x < 3$

查看试题解析
10. 如图所示，正方形 $A B C D$ 的顶点B ， C在x轴的正半轴上，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在第一象限的图．象经过顶点 $A (m ， m + 3)$ 和 $C D$ 上的点E ，且 $O B - C E = 1$ ，过点E的直线l交x轴于点F ，交y轴于点 $G (0 ， - 3)$ ，则 $O F$ 的长为（）

A、 $4.5$ B、5 C、 $5.4$ D、6

查看试题解析

二、填空题

11. 如图，一次函数 $y = - \frac{1}{2} x + b$ 的图象与x轴、y轴分别交于A，B两点，与反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象交于点 $C (- 2 ， 2)$ ，过点B作x轴的平行线交反比例函数的图象于点D，连接CD，则 $△ B C D$ 的面积为．

查看试题解析
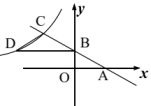12. 已知正比例函数 $y = k x$ 与反比例 $y = \frac{2}{x}$ 函数的图象交于点 $A (1 ， m)$ 和点B，则点B的坐标是．

查看试题解析
13. 两位同学在描述同一反比例函数的图象时，甲同学说：“这个反比例函数图象上任意一点到两坐标轴的距离之积是 $12$ ”．乙同学说：“这个反比例函数图象与直线 $y = x$ 有两个交点”．你认为这两个同学所描绘的反比例函数对应的解析式是．

查看试题解析
14. 为预防传染病，某校定期对教室进行“药熏消毒”.如图所示，药物燃烧阶段，教室内每立方米空气中的含药量 $y (m g)$ 与燃烧时间x（分）成正比例；燃烧后，y与x成反比例.若 $y > 1.6$ ，则x的取值范围是.

查看试题解析
15. 科技小组为了验证某电路的电压 $U (V)$ 、电流 $I (A)$ 电阻 $R (Ω)$ 三者之间的关系： $I = \frac{U}{R}$ ，测得数据如表格：那么，当电阻 $R = 3.6 Ω$ 时，电流 $I =$ A.
$R (Ω)$
2
4
6
9
$I / (A)$
18
9
6
4

查看试题解析
16. 为预防“新冠病毒”，学校对教室喷洒 $84$ 消毒液（含氯消毒剂）进行消杀，资料表明空气中氯含量不低于 $0.5 %$ ，才能有效杀灭新冠病毒．如图，喷洒消毒液时教室空气中的氯含量 $y (%)$ 与时间 $t (m i n)$ 成正比例，消毒液挥发时，y与t成反比例，则此次消杀的有效作用时间是min．

查看试题解析

三、解答题

17. 甲工程队新建公路，每名工人每天工作8小时，则甲工程队每天可完成600米新建公路．乙工程队比甲工程队少10名工人，每名工人每天工作10小时，则乙工程队每天可完成500米新建公路，假定甲、乙两工程队的每名工人每小时完成的工作量相同，求乙工程队的工人有多少名？

查看试题解析
18. 如图，一块砖的A，B，C三个面的面积比是 $4 ： 2 ： 1$ .如果B面向下放在地上，地面所受压强为 $a$ $P a$ ，那么A面和C面分别向下放在地上时，地面所受压强各是多少？

查看试题解析
19. 如图，一次函数 $y_{1} = m x + n$ 的图像与x轴、y轴分别交于A，B两点，与反比例函数 $y_{2} = \frac{k}{x}$ 的图像分别交于C，D两点，已知点C的坐标是 $(1 ， - 3)$ ，且 $A B = 2 B C$ ，求一次函数与反比例函数的解析式．

查看试题解析

四、综合题

20. 一个用电器的电阻是可调节的，其范围为 $110 ~ 220 Ω$ ．已知电压为 $220 V$ ，这个用电器的电路图如图所示．

(1)、功率P与电阻R有怎样的函数关系？

(2)、这个用电器功率的范围是多少？

查看试题解析
21. 如图，取一根长 $100 c m$ 的均匀木杆，用细绳绑在木杆的中点O并将其吊起来.在中点O的左侧挂一个物体，在中点O的右侧用一个弹簧秤向下拉，使木杆处于水平状态.根据杠杆原理，当物体保持不动时，弹簧秤的示数y（单位：N）是x（弹簧秤与中点O的距离）（单位： $c m$ ）的反比例函数，当 $x = 15$ 时， $y = 16$ .

(1)、求y关于x的函数表达式.

(2)、移动弹簧秤的位置，若木杆仍处于水平状态，求弹簧秤的示数 $y$ 的最小值.

查看试题解析
22. 某种气球内充满了一定质量的气体，当温度不变时，气球内气体的压强p（单位： $k P a$ ）是气球的体积V（单位： $d m^{3}$ ）的反比例函数.现测得几组实验数据记录如下：
体积V（单位： $d m^{3}$ ）
…
$1.0$
$1.6$
$2.0$
$2.4$
$3.0$
…
压强p（单位： $k P a$ ）
…
$96$
$60$
$48$
$40$
$32$
…

(1)、求p关于V的函数解析式；

(2)、当气球内气体的压强大于 $120 k P a$ 时，气球将爆炸，为了安全起见，求气球的体积V的最小值.

查看试题解析
23. 我们知道当电压一定时，电流与电阻成反比例函数关系．现有某学生利用一个最大电阻为200欧姆的滑动变阻器及一电流表测电源电压，结果如图所示，当电阻R为6欧姆时，电流I为24安培．

(1)、求电流I（安培）关于电阻R（欧姆）的函数解析式；

(2)、若 $2 \leq R \leq 200$ ，求电流I的变化范围．

查看试题解析
24. 定义：把横、纵坐标均为整数的点称为整点。如图，反比例函数y= $\frac{k}{x}$ (×>0)与正比例函数y=×相交于整点A，与一次函数y=-x+t相交于整点B、C，正比例函数y=x与一次函数y=-x+t相交于点D，线段BC与线段AD上的整点个数之比记作m．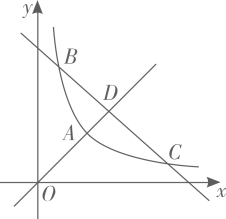

(1)、当k=4时，求D点的坐标和m值．

(2)、当线段BC上的整点个数为7，AD= $\sqrt{2}$ 时，求t的值．

(3)、当AD≤ $\sqrt{2}$ 时，请直接写出t与m之间的关系式．

查看试题解析
25. 已知一次函数 $y_{1} = 3 x - 3$ 的图象与反比例函数 $y_{2} = \frac{m}{x}$ 的图象交于点 $A (a ， 3)$ ， $B (- 1 ， b)$ ．

(1)、求 $a$ ， $b$ 的值和反比例函数的表达式．

(2)、设点 $P (h ， y_{1})$ ， $Q (h ， y_{2})$ 分别是两函数图象上的点 $.$ 在坐标系中画出 $y_{1}$ 和 $y_{2}$ 的图象，并根据图象直接写出，当 $y_{1} > y_{2}$ 时 $h$ 的取值范围；

(3)、设 $k \neq 0$ ，且 $k \neq - 1$ ，当 $x = k$ 时， $y_{2} = p$ ；当 $x = k + 1$ 时， $y_{2} = q .$ 圆圆说：“ $p$ 一定大于 $q$ “ $.$ 你认为圆圆的说法正确吗？为什么？

查看试题解析

体积V（单位： $d m^{3}$ ）	…	$1.0$	$1.6$	$2.0$	$2.4$	$3.0$	…
压强p（单位： $k P a$ ）	…	$96$	$60$	$48$	$40$	$32$	…

$R (Ω)$	2	4	6	9
$I / (A)$	18	9	6	4

2022-2023学年浙教版数学八年级下册6.3反比例函数的应用 课后测验

一、单选题

二、填空题

三、解答题

四、综合题

2022-2023学年浙教版数学八年级下册6.3反比例函数的应用课后测验